![[The AI Show Episode 145]: OpenAI Releases o3 and o4-mini, AI Is Causing “Quiet Layoffs,” Executive Order on Youth AI Education & GPT-4o’s Controversial Update](https://www.marketingaiinstitute.com/hubfs/ep%20145%20cover.png)
![Ditching a Microsoft Job to Enter Startup Purgatory with Lonewolf Engineer Sam Crombie [Podcast #171]](https://cdn.hashnode.com/res/hashnode/image/upload/v1746753508177/0cd57f66-fdb0-4972-b285-1443a7db39fc.png?#)
_Piotr_Adamowicz_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)
_designer491_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)
-xl-xl-xl.jpg)
![Apple Officially Releases macOS Sequoia 15.5 [Download]](https://www.iclarified.com/images/news/97308/97308/97308-640.jpg)
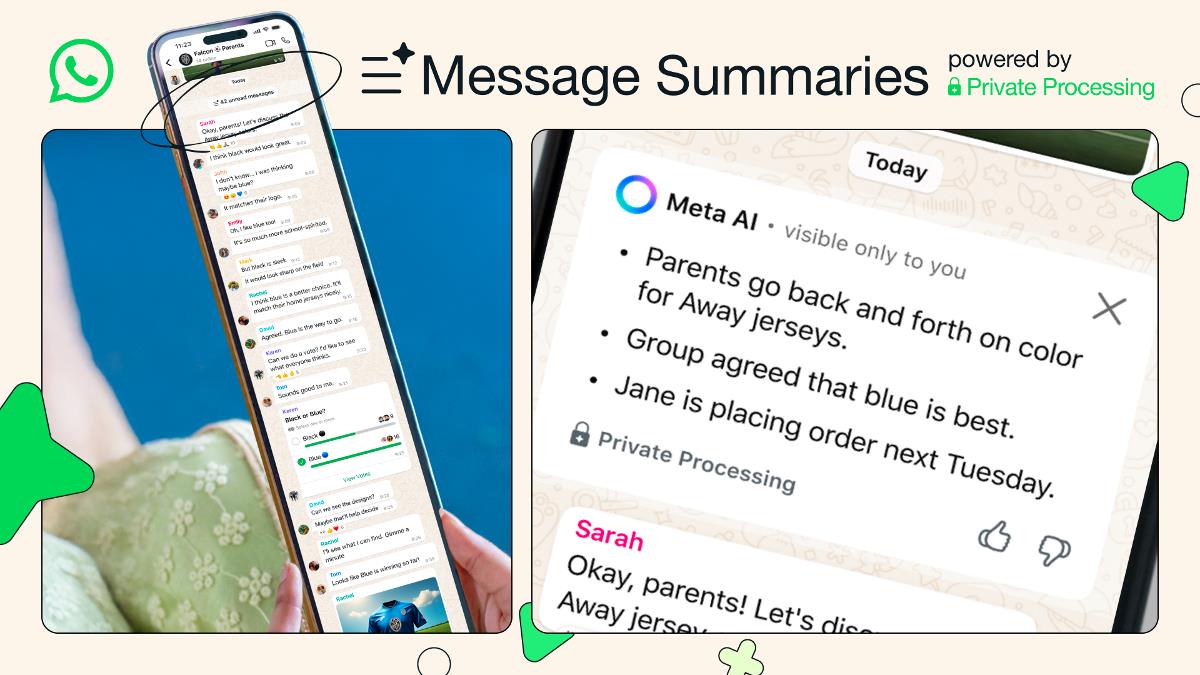
Kernelized Normalizing Constant Estimation: Bridging Bayesian Quadrature and Bayesian Optimization
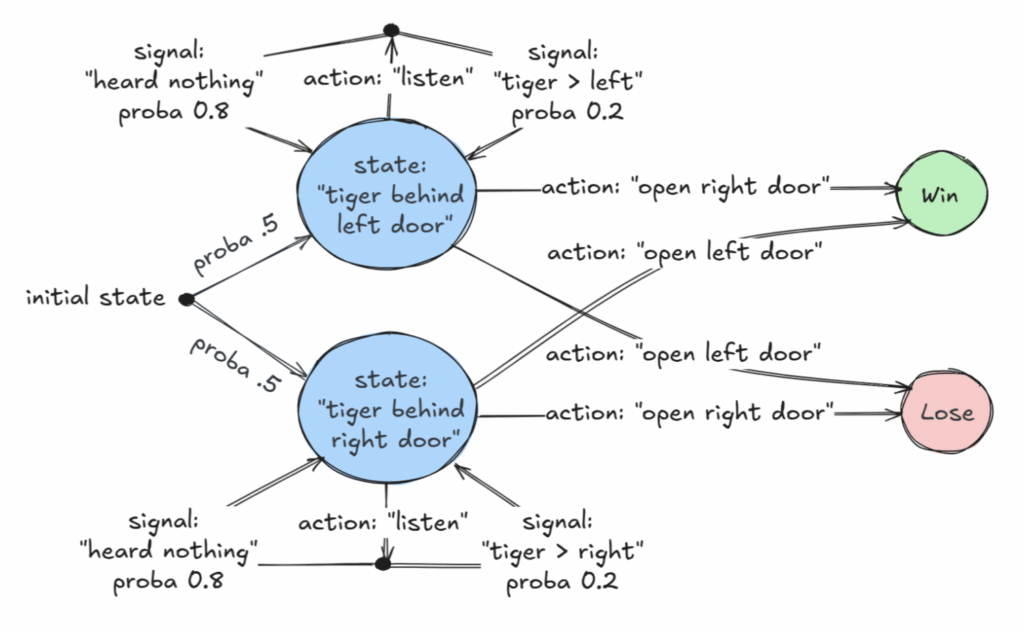
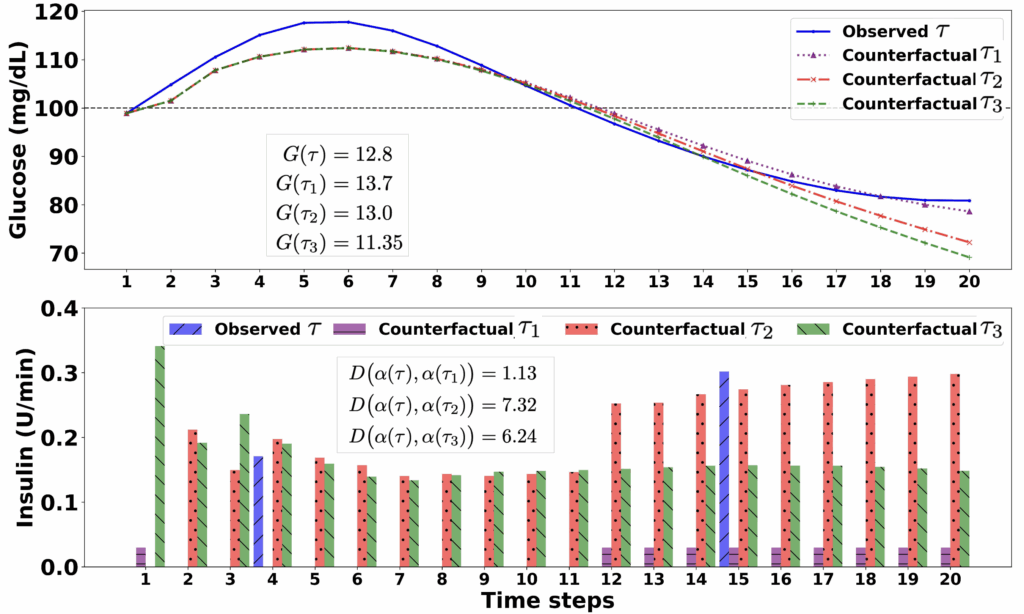
Xu caiが第一著者 In this paper, a normalizing constant on RKHS is considered as follows: Z(f)=∫De−λxdx,λ>0 Z(f) = \int_{D} e^{- \lambda x} dx, \quad \lambda > 0 Z(f)=∫De−λxdx,λ>0 This method considers the lower bound and the upper bound of f∈RKHS f \in RKHS f∈RKHS This method considers the noiseless setting and the noisy setting for the lower bound of f, respectively. Applicable to a multi-layer perception, a point spread function. So authors conducted experiments with various f. Then consider the results with these experiments.
Xu caiが第一著者
In this paper, a normalizing constant on RKHS is considered as follows:
Z(f)=∫De−λxdx,λ>0
Z(f) = \int_{D} e^{- \lambda x} dx, \quad \lambda > 0
Z(f)=∫De−λxdx,λ>0
This method considers the lower bound and the upper bound of
f∈RKHS
f \in RKHS
f∈RKHS
This method considers the noiseless setting and the noisy setting for the lower bound of f, respectively.
Applicable to a multi-layer perception, a point spread function.
So authors conducted experiments with various f.
Then consider the results with these experiments.
