3335. Total Characters in String After Transformations I
3335. Total Characters in String After Transformations I Difficulty: Medium Topics: Hash Table, Math, String, Dynamic Programming, Counting You are given a string s and an integer t, representing the number of transformations to perform. In one transformation, every character in s is replaced according to the following rules: If the character is 'z', replace it with the string "ab". Otherwise, replace it with the next character in the alphabet. For example, 'a' is replaced with 'b', 'b' is replaced with 'c', and so on. Return the length of the resulting string after exactly t transformations. Since the answer may be very large, return it modulo 109 + 7. Example 1: Input: s = "abcyy", t = 2 Output: 7 Explanation: First Transformation (t = 1): 'a' becomes 'b' 'b' becomes 'c' 'c' becomes 'd' 'y' becomes 'z' 'y' becomes 'z' String after the first transformation: "bcdzz" Second Transformation (t = 2): 'b' becomes 'c' 'c' becomes 'd' 'd' becomes 'e' 'z' becomes "ab" 'z' becomes "ab" String after the second transformation: "cdeabab" Final Length of the string: The string is "cdeabab", which has 7 characters. Example 2: Input: s = "azbk", t = 1 Output: 5 Explanation: First Transformation (t = 1): 'a' becomes 'b' 'z' becomes "ab" 'b' becomes 'c' 'k' becomes 'l' String after the first transformation: "babcl" Final Length of the string: The string is "babcl", which has 5 characters. Constraints: 1
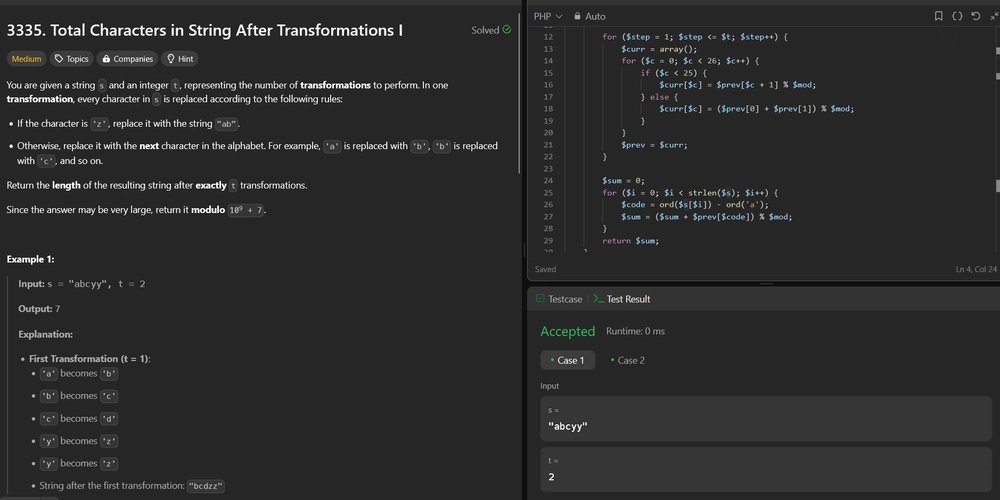
3335. Total Characters in String After Transformations I
Difficulty: Medium
Topics: Hash Table, Math, String, Dynamic Programming, Counting
You are given a string s and an integer t, representing the number of transformations to perform. In one transformation, every character in s is replaced according to the following rules:
- If the character is
'z', replace it with the string"ab". - Otherwise, replace it with the next character in the alphabet. For example,
'a'is replaced with'b','b'is replaced with'c', and so on.
Return the length of the resulting string after exactly t transformations.
Since the answer may be very large, return it modulo 109 + 7.
Example 1:
- Input: s = "abcyy", t = 2
- Output: 7
-
Explanation:
-
First Transformation (t = 1):
-
'a'becomes'b' -
'b'becomes'c' -
'c'becomes'd' -
'y'becomes'z' -
'y'becomes'z' - String after the first transformation:
"bcdzz"
-
-
Second Transformation (t = 2):
-
'b'becomes'c' -
'c'becomes'd' -
'd'becomes'e' -
'z'becomes"ab" -
'z'becomes"ab" - String after the second transformation:
"cdeabab"
-
-
Final Length of the string: The string is
"cdeabab", which has 7 characters.
-
First Transformation (t = 1):
Example 2:
- Input: s = "azbk", t = 1
- Output: 5
-
Explanation:
-
First Transformation (t = 1):
-
'a'becomes'b' -
'z'becomes"ab" -
'b'becomes'c' -
'k'becomes'l' - String after the first transformation:
"babcl"
-
-
Final Length of the string: The string is
"babcl", which has 5 characters.
-
First Transformation (t = 1):
Constraints:
1 <= s.length <= 105-
sconsists only of lowercase English letters. 1 <= t <= 105
Hint:
- Maintain the frequency of each character.
Solution:
We need to determine the length of a string after applying a specified number of transformations. Each transformation follows specific rules where characters are incremented to the next letter in the alphabet, except for 'z', which is replaced by "ab". Given the constraints, a direct simulation approach is infeasible, so we use dynamic programming to efficiently compute the result.
Approach
- Dynamic Programming (DP) Setup: We use a DP array to track the number of characters generated by each starting character after each transformation step.
-
State Transition: For each character and each transformation step, compute the number of characters generated:
- If the character is not 'z', it simply increments to the next character.
- If the character is 'z', it splits into 'a' and 'b', which are then processed in subsequent steps.
- Efficient Computation: By precomputing the DP values for all characters up to the given number of transformations, we can quickly sum the contributions of each character in the input string.
Let's implement this solution in PHP: 3335. Total Characters in String After Transformations I
/**
* @param String $s
* @param Integer $t
* @return Integer
*/
function lengthAfterTransformations($s, $t) {
$mod = 1000000007;
$prev = array_fill(0, 26, 1); // Represents dp[0] (t=0)
for ($step = 1; $step <= $t; $step++) {
$curr = array();
for ($c = 0; $c < 26; $c++) {
if ($c < 25) {
$curr[$c] = $prev[$c + 1] % $mod;
} else {
$curr[$c] = ($prev[0] + $prev[1]) % $mod;
}
}
$prev = $curr;
}
$sum = 0;
for ($i = 0; $i < strlen($s); $i++) {
$code = ord($s[$i]) - ord('a');
$sum = ($sum + $prev[$code]) % $mod;
}
return $sum;
}
// Example Test Cases
echo lengthAfterTransformations("abcyy", 2) . "\n"; // Output: 7
echo lengthAfterTransformations("azbk", 1) . "\n"; // Output: 5
?>
Explanation:
-
Initialization: Start with an array
previnitialized to 1 for all characters, representing the count of each character after 0 transformations. -
DP Array Update: For each transformation step, compute the new counts (
curr) based on the previous step's counts (prev). For non-'z' characters, the count is simply the count of the next character from the previous step. For 'z', the count is the sum of the counts of 'a' and 'b' from the previous step. -
Summing Results: After computing the DP array up to
ttransformations, sum the contributions of each character in the input string using the precomputed DP values, taking modulo 109 + 7 to handle large numbers.
This approach efficiently computes the result in O(26 x t) time and O(26) space, making it feasible for large values of t up to 105.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks










































































































































































![[The AI Show Episode 156]: AI Answers - Data Privacy, AI Roadmaps, Regulated Industries, Selling AI to the C-Suite & Change Management](https://www.marketingaiinstitute.com/hubfs/ep%20156%20cover.png)
![[The AI Show Episode 155]: The New Jobs AI Will Create, Amazon CEO: AI Will Cut Jobs, Your Brain on ChatGPT, Possible OpenAI-Microsoft Breakup & Veo 3 IP Issues](https://www.marketingaiinstitute.com/hubfs/ep%20155%20cover.png)



















































































































![Rust VS Go VS TypeScript – which back end language is for you? With Tai Groot [Podcast #176]](https://cdn.hashnode.com/res/hashnode/image/upload/v1750974265013/73f79068-0087-4c39-8a8b-feea8cac873b.png?#)














































































































.jpg?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)