การทำนายหรือการคาดเดาราคาบ้านจาก Machine Learning ด้วย Linear Regression

ในการทำนายหรือการคาดเดา "ราคาบ้าน" นั้นต้องมีเครื่องมือสำคัญที่ช่วยให้การตัดสินใจและจัดการกับข้อมูลหลายมิติ เช่น ทำเลที่ตั้ง จำนวนห้อง หรือรายได้เฉลี่ยของผู้อยู่อาศัย ซึ่งความซับซ้อนที่เพิ่มขึ้นนี้ จึงมีการนำเทคนิค Machine Learning เข้ามาช่วยวิเคราะห์ หนึ่งในวิธีที่เรียบง่ายแต่มีประสิทธิภาพคือ Linear Regression ซึ่งเป็นการคำนวณหาความสัมพันธ์ระหว่างตัวแปรต้น (Predictor: x) และตัวแปรตาม (Response: y) โดยอิงจากแนวโน้มเชิงเส้นที่มีความเข้าใจง่าย และสามารถประยุกต์ใช้ได้หลากหลาย โดยเฉพาะในงานทำนายราคาบ้านที่ต้องอาศัยทั้งข้อมูลเชิงตัวเลขและคุณลักษณะเชิงคุณภาพ ในบทความนี้ เราจะพาคุณไปรู้จักการสร้างแบบจำลองเพื่อทำนายราคาบ้านด้วยเทคนิค Linear Regression พร้อมทั้งสาธิตการใช้งานจริงผ่าน Google Colab ซึ่งอ้างอิงจากบทความ "House Price Prediction with Machine Learning" โดยคุณ Varun Tyagi แบบจำลองนี้ใช้ชุดข้อมูล California Housing Dataset ซึ่งเป็นข้อมูลจากการสำรวจสำมะโนประชากรของสหรัฐอเมริกา (U.S. Census) ในปี 1990 โดยเน้นพื้นที่ในรัฐแคลิฟอร์เนีย ประกอบไปด้วย ชุดข้อมูล 8 ตัวแปรต้น [, 1] MedInc คือ รายได้เฉลี่ยต่อครัวเรือนในเขตนั้น (หน่วย: 10,000 ดอลลาร์สหรัฐ) [, 2] HouseAge คือ อายุเฉลี่ยของบ้านในเขตนั้น (หน่วย: ปี) [, 3] AveRooms คือ จำนวนห้องเฉลี่ยต่อบ้าน [, 4] AveBedrms คือ จำนวนห้องนอนเฉลี่ยต่อบ้าน [, 5] Population คือ จำนวนประชากรในเขตนั้น [, 6] AveOccup คือ จำนวนผู้อยู่อาศัยเฉลี่ยต่อบ้าน [, 7] Latitude คือ ละติจูด (พิกัดที่ตั้งบ้าน) [, 8] Longitude คือ ลองจิจูด (พิกัดที่ตั้งบ้าน) และ 1 ตัวแปรตาม [, 9] MEDV คือ ราคากลางของบ้านในเขตนั้น (หน่วย: 100,000 ดอลลาร์สหรัฐ) การนำเข้าไลบรารีที่จำเป็น ไลบรารีเหล่านี้ใช้สำหรับการจัดการข้อมูล สร้าง และประเมินผลแบบจำลอง import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.datasets import fetch_california_housing โหลดชุดข้อมูลและสร้าง DataFrame: สามารถโหลดข้อมูลและสร้าง DataFrame พร้อมเพิ่มคอลัมน์ MEDV ซึ่งแสดงถึงราคากลางของบ้านในแต่ละเขตได้ดังนี้: #Download the California Housing dataset california_housing = fetch_california_housing() data = pd.DataFrame(california_housing.data, columns=california_housing.feature_names) #Median house value for California districts data['MEDV'] = california_housing.target data.head(10) ตัวอย่างผลที่ได้จาก code การจัดข้อมูลให้เหมาะสม และทำการวิเคราะห์ข้อมูลเบื้องต้น สร้างกราฟที่แสดงความสัมพันธ์ระหว่างค่า Median Income (MedInc) และ Median House Value (MEDV) โดยใช้ Matplotlib และคำนวณ ค่าสหสัมพันธ์ (correlation) ระหว่างสองตัวแปรนี้ plt.scatter(data['MedInc'], data['MEDV'], alpha=0.5) plt.title('Relationship between Median House Value and Median Income') plt.xlabel('Median Income') plt.ylabel('Median House Value') correlation = data['MedInc'].corr(data['MEDV']) print("Correlation :", correlation) plt.show() ตัวอย่างผลที่ได้จาก code การแบ่งข้อมูลออกเป็นชุดฝึก (Training Set) และชุดทดสอบ (Test Set) ใช้ฟังก์ชัน train_test_split เพื่อแบ่งข้อมูลออกเป็น 2 ส่วน คือ ชุดฝึก (80%) และชุดทดสอบ (20%) X_train, X_test, y_train, y_test = train_test_split( data.drop('MEDV', axis=1), data['MEDV'], test_size=0.2, random_state=42) เตรียมข้อมูลสำหรับโมเดลที่ต้องการใช้ข้อมูล MedInc (รายได้เฉลี่ย)และเพื่อทำนาย MEDV (ค่าบ้านเฉลี่ย) ในการฝึกโมเดล X = data[['MedInc']] y = data['MEDV'] ฝึกโมเดล Linear Regression โดยใช้ข้อมูล MedInc โมเดลนี้จะช่วยให้เราเข้าใจว่า "รายได้เฉลี่ยของครัวเรือน" (MedInc) ส่งผลอย่างไรต่อ "ราคาบ้านเฉลี่ย" (MEDV) โดยสมมติความสัมพันธ์เป็นเชิงเส้น (Linear) from sklearn import linear_model as lm model = lm.LinearRegression() results = model.fit(X,y) print(model.intercept_, model.coef_) ผลที่ได้จะเป็นค่า Intercept และ Coefficient ของ regression model การปรับสเกลข้อมูลเชิงตัวเลขด้วย StandardScaler ทำ feature scaling กับตัวแปรเชิงตัวเลข เพื่อให้โมเดลเรียนรู้ได้แม่นยำและรวดเร็วขึ้น โดยใช้ StandardScaler ผ่าน ColumnTransformer numerical_features = X_train.columns.difference(['Description']) preprocessor = ColumnTransformer( transformers=[ ('num', StandardScaler(), X_train.columns.difference(['Description'])), ] ) แต่ในกรณีนี้คอลัมน์ Description จะไม่ถูกปรับสเกล เนื่องจากเป็นข้อมูลที่ไม่ใช่ตัวเลข สร้าง Pipeline เพื่อรวมการแปลงข้อมูลและการฝึกโมเดลไว้ในขั้นตอนเดียว Pipeline ช่วยให้การเทรนโมเดลอยู่ในกระบวนการเดียวกัน และลดความผิดพลาดได้ดี model = make_pipeline(preprocessor, LinearRegression()) # Train the model model.fit(X_train, y_train) ทำนายและประเมินผลโมเดล Linear Regression นำโมเดลไปใช้กับชุดข้อมูลทดสอบ (X_test) เพื่อทำนายราคาบ้าน (y_pred) และประเมินผลลัพธ์ที่ได้ด้วย Mean Squared Error (MSE) เพื่อให้ทราบว่าโมเดลทำงานได้ดีแค่ไหน y_pred = model.predict(X_test) mse = mean_squared_error(y_test, y_pred) print(f'Mean Squared Error on Test Data: {mse}') # Save the model for future use joblib.dump(model, 'housing_price_model.joblib') ไฟล์ housing_price_model.joblib นี้สา

Apr 11, 2025 - 11:29

การทำนายหรือการคาดเดาราคาบ้านจาก Machine Learning ด้วย Linear Regression

ในการทำนายหรือการคาดเดา "ราคาบ้าน" นั้นต้องมีเครื่องมือสำคัญที่ช่วยให้การตัดสินใจและจัดการกับข้อมูลหลายมิติ เช่น ทำเลที่ตั้ง จำนวนห้อง หรือรายได้เฉลี่ยของผู้อยู่อาศัย ซึ่งความซับซ้อนที่เพิ่มขึ้นนี้ จึงมีการนำเทคนิค Machine Learning เข้ามาช่วยวิเคราะห์

หนึ่งในวิธีที่เรียบง่ายแต่มีประสิทธิภาพคือ Linear Regression ซึ่งเป็นการคำนวณหาความสัมพันธ์ระหว่างตัวแปรต้น (Predictor: x) และตัวแปรตาม (Response: y) โดยอิงจากแนวโน้มเชิงเส้นที่มีความเข้าใจง่าย และสามารถประยุกต์ใช้ได้หลากหลาย โดยเฉพาะในงานทำนายราคาบ้านที่ต้องอาศัยทั้งข้อมูลเชิงตัวเลขและคุณลักษณะเชิงคุณภาพ

ในบทความนี้ เราจะพาคุณไปรู้จักการสร้างแบบจำลองเพื่อทำนายราคาบ้านด้วยเทคนิค Linear Regression พร้อมทั้งสาธิตการใช้งานจริงผ่าน Google Colab ซึ่งอ้างอิงจากบทความ "House Price Prediction with Machine Learning" โดยคุณ Varun Tyagi

แบบจำลองนี้ใช้ชุดข้อมูล California Housing Dataset ซึ่งเป็นข้อมูลจากการสำรวจสำมะโนประชากรของสหรัฐอเมริกา (U.S. Census) ในปี 1990 โดยเน้นพื้นที่ในรัฐแคลิฟอร์เนีย ประกอบไปด้วย

ชุดข้อมูล 8 ตัวแปรต้น
[, 1] MedInc คือ รายได้เฉลี่ยต่อครัวเรือนในเขตนั้น (หน่วย: 10,000 ดอลลาร์สหรัฐ)
[, 2] HouseAge คือ อายุเฉลี่ยของบ้านในเขตนั้น (หน่วย: ปี)
[, 3] AveRooms คือ จำนวนห้องเฉลี่ยต่อบ้าน
[, 4] AveBedrms คือ จำนวนห้องนอนเฉลี่ยต่อบ้าน
[, 5] Population คือ จำนวนประชากรในเขตนั้น
[, 6] AveOccup คือ จำนวนผู้อยู่อาศัยเฉลี่ยต่อบ้าน
[, 7] Latitude คือ ละติจูด (พิกัดที่ตั้งบ้าน)
[, 8] Longitude คือ ลองจิจูด (พิกัดที่ตั้งบ้าน)

และ 1 ตัวแปรตาม
[, 9] MEDV คือ ราคากลางของบ้านในเขตนั้น (หน่วย: 100,000 ดอลลาร์สหรัฐ)

การนำเข้าไลบรารีที่จำเป็น

ไลบรารีเหล่านี้ใช้สำหรับการจัดการข้อมูล สร้าง และประเมินผลแบบจำลอง

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing

โหลดชุดข้อมูลและสร้าง DataFrame:

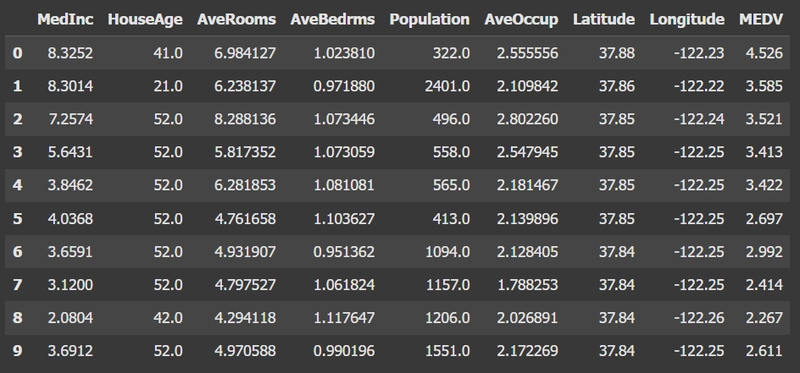
สามารถโหลดข้อมูลและสร้าง DataFrame พร้อมเพิ่มคอลัมน์ MEDV ซึ่งแสดงถึงราคากลางของบ้านในแต่ละเขตได้ดังนี้:

#Download the California Housing dataset
california_housing = fetch_california_housing()
data = pd.DataFrame(california_housing.data, columns=california_housing.feature_names)

#Median house value for California districts
data['MEDV'] = california_housing.target  
data.head(10)

ตัวอย่างผลที่ได้จาก code

การจัดข้อมูลให้เหมาะสม และทำการวิเคราะห์ข้อมูลเบื้องต้น

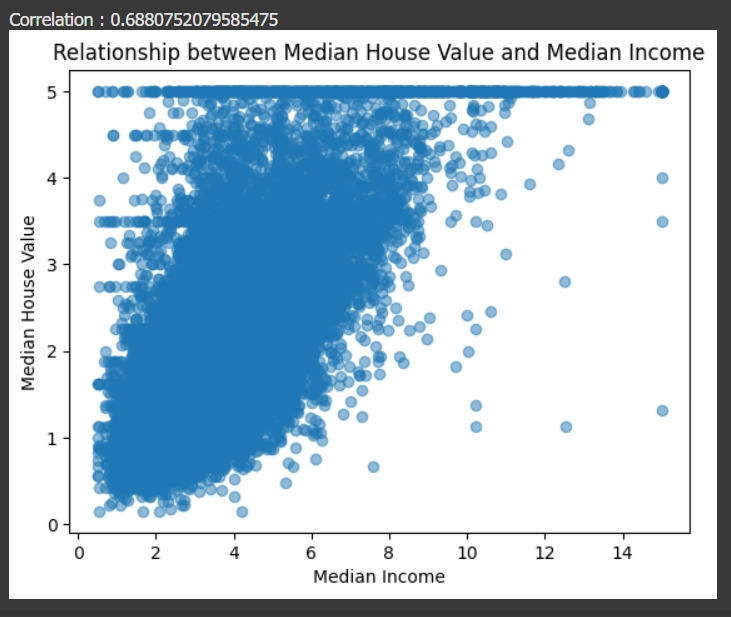
สร้างกราฟที่แสดงความสัมพันธ์ระหว่างค่า Median Income (MedInc) และ Median House Value (MEDV) โดยใช้ Matplotlib และคำนวณ ค่าสหสัมพันธ์ (correlation) ระหว่างสองตัวแปรนี้

plt.scatter(data['MedInc'], data['MEDV'], alpha=0.5)
plt.title('Relationship between Median House Value and Median Income')
plt.xlabel('Median Income')
plt.ylabel('Median House Value')
correlation = data['MedInc'].corr(data['MEDV'])
print("Correlation :", correlation)
plt.show()

ตัวอย่างผลที่ได้จาก code

การแบ่งข้อมูลออกเป็นชุดฝึก (Training Set) และชุดทดสอบ (Test Set)

ใช้ฟังก์ชัน train_test_split เพื่อแบ่งข้อมูลออกเป็น 2 ส่วน คือ ชุดฝึก (80%) และชุดทดสอบ (20%)

X_train, X_test, y_train, y_test = train_test_split(
    data.drop('MEDV', axis=1), data['MEDV'], test_size=0.2, random_state=42)

เตรียมข้อมูลสำหรับโมเดลที่ต้องการใช้ข้อมูล MedInc (รายได้เฉลี่ย)และเพื่อทำนาย MEDV (ค่าบ้านเฉลี่ย) ในการฝึกโมเดล

X = data[['MedInc']]   
y = data['MEDV']

ฝึกโมเดล Linear Regression โดยใช้ข้อมูล MedInc

โมเดลนี้จะช่วยให้เราเข้าใจว่า "รายได้เฉลี่ยของครัวเรือน" (MedInc) ส่งผลอย่างไรต่อ "ราคาบ้านเฉลี่ย" (MEDV) โดยสมมติความสัมพันธ์เป็นเชิงเส้น (Linear)

from sklearn import linear_model as lm

model = lm.LinearRegression()
results = model.fit(X,y)

print(model.intercept_, model.coef_)

ผลที่ได้จะเป็นค่า Intercept และ Coefficient ของ regression model

การปรับสเกลข้อมูลเชิงตัวเลขด้วย StandardScaler

ทำ feature scaling กับตัวแปรเชิงตัวเลข เพื่อให้โมเดลเรียนรู้ได้แม่นยำและรวดเร็วขึ้น โดยใช้ StandardScaler ผ่าน ColumnTransformer

numerical_features = X_train.columns.difference(['Description'])
preprocessor = ColumnTransformer(
    transformers=[
        ('num', StandardScaler(), X_train.columns.difference(['Description'])),
    ]
)

แต่ในกรณีนี้คอลัมน์ Description จะไม่ถูกปรับสเกล เนื่องจากเป็นข้อมูลที่ไม่ใช่ตัวเลข

สร้าง Pipeline เพื่อรวมการแปลงข้อมูลและการฝึกโมเดลไว้ในขั้นตอนเดียว

Pipeline ช่วยให้การเทรนโมเดลอยู่ในกระบวนการเดียวกัน และลดความผิดพลาดได้ดี

model = make_pipeline(preprocessor, LinearRegression())

# Train the model
model.fit(X_train, y_train)

ทำนายและประเมินผลโมเดล Linear Regression

นำโมเดลไปใช้กับชุดข้อมูลทดสอบ (X_test) เพื่อทำนายราคาบ้าน (y_pred) และประเมินผลลัพธ์ที่ได้ด้วย Mean Squared Error (MSE) เพื่อให้ทราบว่าโมเดลทำงานได้ดีแค่ไหน

y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error on Test Data: {mse}')

# Save the model for future use
joblib.dump(model, 'housing_price_model.joblib')

ไฟล์ housing_price_model.joblib นี้สามารถโหลดกลับมาใช้ทำนายใหม่ได้ทันที ด้วย joblib.load()

ผลลัพธ์ของโค้ดคือค่า Mean Squared Error on Test Data: 0.5558915986952442
ค่า MSE ที่ต่ำแสดงว่าโมเดลสามารถทำนายราคาบ้านได้ใกล้เคียงกับค่าจริงพอสมควร

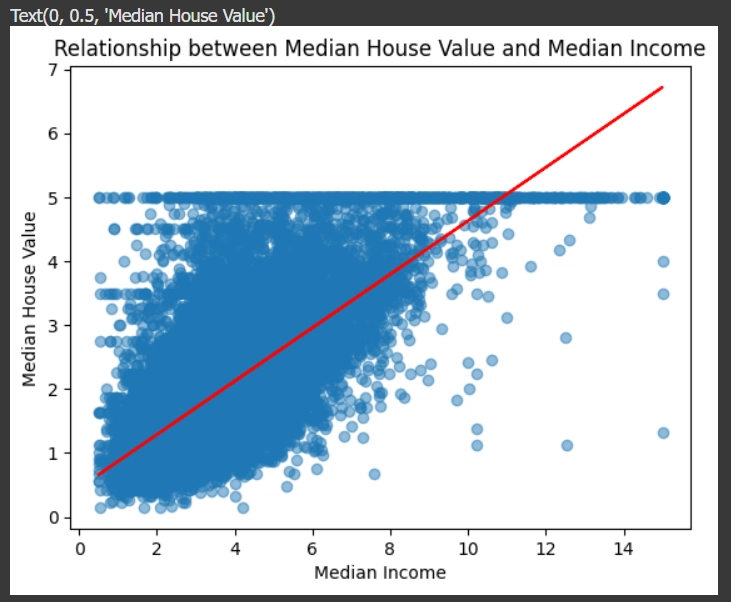
plot graph Scatter Plot พร้อมเส้นแนวโน้ม (Trend Line)

แสดงความสัมพันธ์ระหว่างรายได้เฉลี่ย (MedInc) กับราคาบ้านเฉลี่ย (MEDV)

plt.scatter(data['MedInc'], data['MEDV'], alpha=0.5)

# คำนวณเส้นแนวโน้ม (trend line)
m, b = np.polyfit(data['MedInc'], data['MEDV'], 1)  # m = slope, b = intercept

plt.plot(data['MedInc'], m * data['MedInc'] + b, color='red', label='Trend Line')

plt.title('Relationship between Median House Value and Median Income')
plt.xlabel('Median Income')
plt.ylabel('Median House Value')

ผลที่ได้

ทำนายราคาบ้านใหม่ด้วยโมเดลที่ฝึกไว้แล้ว

เราจะได้รับข้อมูลของบ้านใหม่ที่ต้องการทำนายราคา ด้วยการโหลดโมเดลที่ฝึกไว้จากไฟล์ .joblib แล้วทำการทำนายราคาบ้านใหม่
** ราคาที่ได้จะคูณด้วย 100000 เพราะว่าโมเดลอาจจะทำนายราคาบ้านในหน่วยที่เล็กกว่าจึงต้องแปลงเป็นราคาบ้านในหน่วยเงินของสกุลเงินดอลลาร์**

new_house = pd.DataFrame({
    'MedInc': [3.0],  # Example numerical features, use appropriate values from the dataset
    'HouseAge': [20.0],
    'AveRooms': [5.0],
    'AveBedrms': [2.0],
    'Population': [1000.0],
    'AveOccup': [3.0],
    'Latitude': [37.5],
    'Longitude': [-122.5],
    'Description': ["Charming cottage with a garden"]  # Example text feature
})

# Load the pre-trained model
loaded_model = joblib.load('housing_price_model.joblib')

# Make predictions for the new house
predicted_price = loaded_model.predict(new_house) * 100000
print(f'Predicted Price for the New House: ${predicted_price[0]:.2f}')

โมเดลทำนายราคาบ้านใหม่ที่ประมาณการได้อยู่ที่ $284,131.64

ตัวอย่างเพิ่มเติม

โดยในตัวอย่างข้อมูลเพิ่มเติม เราจะใช้ข้อมูลของ Diabetes Dataset เป็นชุดข้อมูลที่การวัดความเปลี่ยนแปลงของระดับน้ำตาลในเลือดของผู้ป่วยในช่วงระยะเวลา 1 ปี โดยการทำนายนี้จะเป็น การทำนายเชิงปริมาณ (regression) ซึ่งให้ค่าเป็นตัวเลขที่แสดงถึงการพัฒนา (progression) ของโรคเบาหวาน

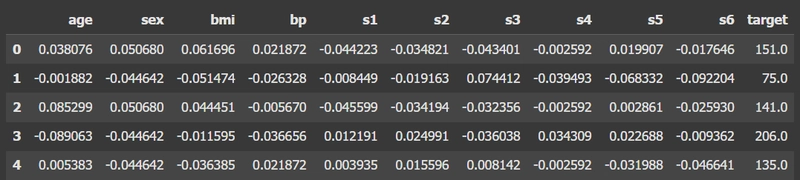
ข้อมูล Diabetes Dataset ประกอบด้วยจำนวนแถว (Rows): 442 แถว จำนวนคอลัมน์ (Columns) 11 คอลัมน์ เป็น10 ตัวแปรต้น + 1 ตัวแปรเป้าหมาย (target)

[, 1] age อายุของผู้ป่วย (normalized)
[, 2] sex เพศ (normalized)
[, 3] bmi Body Mass Index (ค่าดัชนีมวลกาย)
[, 4] bp Blood Pressure (ค่าความดันโลหิตเฉลี่ย)
[, 5] s1 ค่าทางชีวเคมีในเลือดที่ 1
[, 6] s2 ค่าทางชีวเคมีในเลือดที่ 2
[, 7] s3 ค่าทางชีวเคมีในเลือดที่ 3
[, 8] s4 ค่าทางชีวเคมีในเลือดที่ 4
[, 9] s5 ค่าทางชีวเคมีในเลือดที่ 5
[, 10] s6 ค่าทางชีวเคมีในเลือดที่ 6
[, 11] target ความก้าวหน้าของโรคเบาหวาน (progression) ซึ่งใช้เป็นค่าที่เราต้องการทำนาย

การนำเข้าไลบรารีที่จำเป็น

ไลบรารีเหล่านี้ใช้สำหรับการจัดการข้อมูล สร้าง และประเมินผลแบบจำลอง

# Import the libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

โหลดชุดข้อมูลและสร้าง DataFrame:

diabetes = datasets.load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df['target'] = diabetes.target
df.head()

ตัวอย่างผลที่ได้จาก code

การจัดข้อมูลให้เหมาะสม และทำการวิเคราะห์ข้อมูลเบื้องต้น

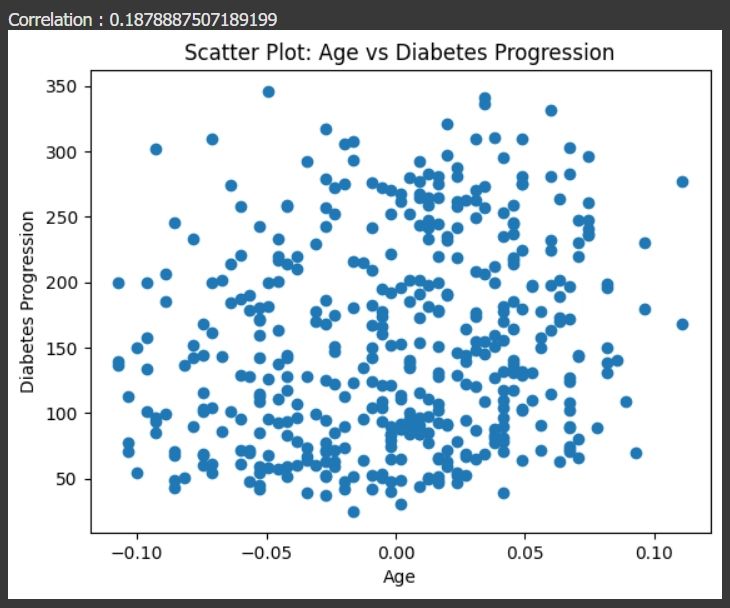
หา Correlation และทำการวาดกราฟเพื่อดูความสัมพันธ์ระหว่างอายุ (Age) และ (Diabetes Progression) ค่าการพัฒนาของโรคเบาหวาน

plt.scatter(df['age'], y=df['target'])
plt.title('Scatter Plot: Age vs Diabetes Progression')
plt.xlabel('Age')
plt.ylabel('Diabetes Progression')
correlation =df['age'].corr(df['target'])
print("Correlation :", correlation)
plt.show()

รูปกราฟที่ได้และค่า correlation

การแบ่งข้อมูลออกเป็นชุดฝึก (Training Set) และชุดทดสอบ (Test Set)

เตรียมข้อมูลโดยแยก Features (X) และ Target (y) จากข้อมูลที่โหลดมา แล้วใช้ train_test_split ในการแบ่งข้อมูลออกเป็นชุดฝึก (train) และชุดทดสอบ (test)

X = df.drop('target', axis=1)
y = df['target']

# แบ่งข้อมูลเป็นชุด train/test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

ฝึกโมเดล Linear Regression และแสดงค่า intercept และ coefficients ของโมเดล

ฝึกโมเดล model.fit() โดยใช้ข้อมูล X (features) และ y (target) ที่เตรียมไว้

from sklearn import linear_model as lm

model = lm.LinearRegression()
results = model.fit(X,y)

print(model.intercept_, model.coef_)

ผลที่ได้จะเป็นค่า Intercept และ Coefficient ของ regression model

Intercept (ค่าคงที่): 152.13
Coefficients (สัมประสิทธิ์ของแต่ละฟีเจอร์):
[ -10.01, -239.82, 519.85, 324.38, -792.18, 476.74, 101.04,...]

ทำนายและประเมินผลโมเดล Linear Regression

นำเข้าโมดูล joblibซึ่งใช้สำหรับ บันทึก (save) และ โหลด (load) โมเดลที่ฝึกไว้แล้ว

คำนวณ Mean Squared Error (MSE) ซึ่งเป็นค่าความคลาดเคลื่อนระหว่างค่าจริง

บันทึกโมเดล ที่ฝึกไว้แล้วลงไฟล์ชื่อ diabetes_model.joblib

import joblib
y_pred = model.predict(X_test)

mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error on Test Data: {mse}')

joblib.dump(model, 'diabetes_model.joblib')

ผลลัพธ์ของโค้ดคือค่า Mean Squared Error on Test Data: 2900.1936284934823

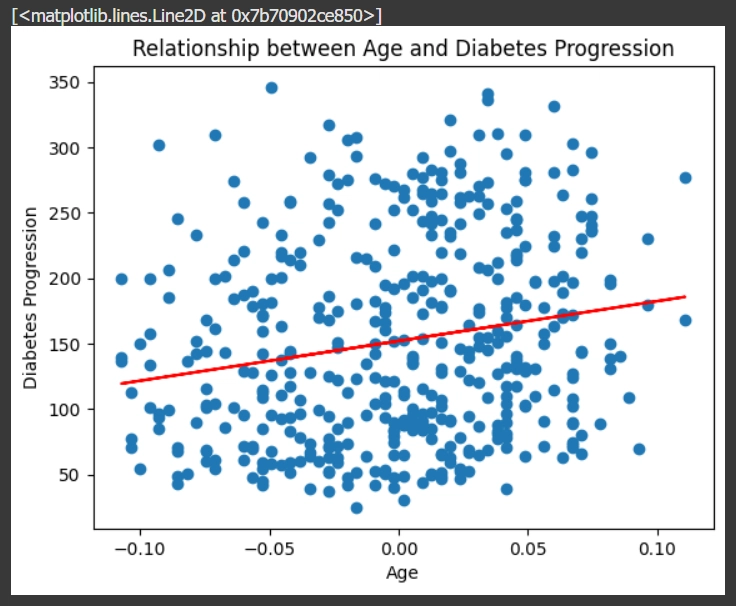
plot graph Scatter Plot พร้อมเส้นแนวโน้ม (Trend Line)

แสดงความสัมพันธ์ระหว่างอายุ (Age) และ (Diabetes Progression) ค่าการพัฒนาของโรคเบาหวาน

plt.scatter(df['age'], df['target'])
plt.title('Relationship between Age and Diabetes Progression')
plt.xlabel('Age')
plt.ylabel('Diabetes Progression')

m, b = np.polyfit(df['age'], df['target'], 1)  # m = slope, b = intercept
plt.plot(df['age'], m * df['age'] + b, color='red', label='Trend Line')

ผลที่ได้

ทำนายค่าใหม่ด้วยโมเดลที่ฝึกไว้แล้ว

สำหรับ new_patient เป็นข้อมูลจำลองของผู้ป่วยใหม่ 1 คน

โหลดโมเดล LinearRegression ที่ถูก train ด้วย Diabetes Dataset
ส่งข้อมูลผู้ป่วย new_patient เข้าโมเดลเพื่อทำนายค่า target
ได้target ที่เป็นค่าการพัฒนาโรคเบาหวานในอีก 1 ปีข้างหน้า (จาก dataset ของ scikit-learn)

new_patient = pd.DataFrame({
    'age': [0.038076],
    'sex': [0.050680],
    'bmi': [-0.036385],
    'bp': [0.021872],
    's1': [0.012191],
    's2': [ -0.019163],
    's3': [ -0.036038],
    's4': [0.002861],
    's5': [0.022688],
    's6': [-0.092204],
})

loaded_model = joblib.load('diabetes_model.joblib')

predicted_target = loaded_model.predict(new_patient)

print(f'Predicted Diabetes Progression: {predicted_target[0]:.2f}')

โมเดลทำนายการพัฒนาของโรคเบาหวานได้ค่า Predicted Diabetes Progression: 114.22

ซึ่งค่าปกติจาก dataset นี้มีค่าเฉลี่ยประมาณ 150-170 ดังนั้น ค่า 114.22 ถือว่าอยู่ในระดับ ต่ำกว่าค่าเฉลี่ย แสดงว่าผู้ป่วยรายนี้มีแนวโน้ม พัฒนาการของโรคเบาหวานไม่รุนแรงมาก

สรุปผล

สำหรับบทความนี้ เราได้แสดงตัวอย่างการนำเทคนิค Linear Regression มาใช้ในการวิเคราะห์และทำนายข้อมูลจาก 2 ชุดข้อมูล ได้แก่ California Housing Dataset และ Diabetes Dataset ซึ่งครอบคลุมทั้งการประเมินราคาบ้านตามปัจจัยต่าง ๆ และการทำนายระดับการพัฒนาโรคเบาหวานในผู้ป่วย

โดยโครงสร้างของข้อมูลเบื้องต้น จะวิเคราะห์ความสัมพันธ์ของฟีเจอร์ผ่านกราฟ scatter plot และทำการสร้างโมเดลโดยใช้ LinearRegression จาก scikit-learn พร้อมทั้งทดสอบประสิทธิภาพของโมเดลด้วยค่า Mean Squared Error (MSE) นอกจากนี้ เรายังได้ลองนำโมเดลที่ฝึกไว้แล้วมาใช้ในการ ทำนายค่าจากข้อมูลของผู้ป่วยหรือบ้านรายใหม่ เพื่อจำลองการใช้งานจริง

แหล่งข้อมูลอ้างอิง : https://medium.com/@varun.tyagi83/house-price-prediction-with-machine-learning-d49f93d681f2
แหล่งข้อมูลอ้างอิง : https://www.kaggle.com/code/meet3010/linear-regression-on-the-diabetes-dataset