Statistics Basics
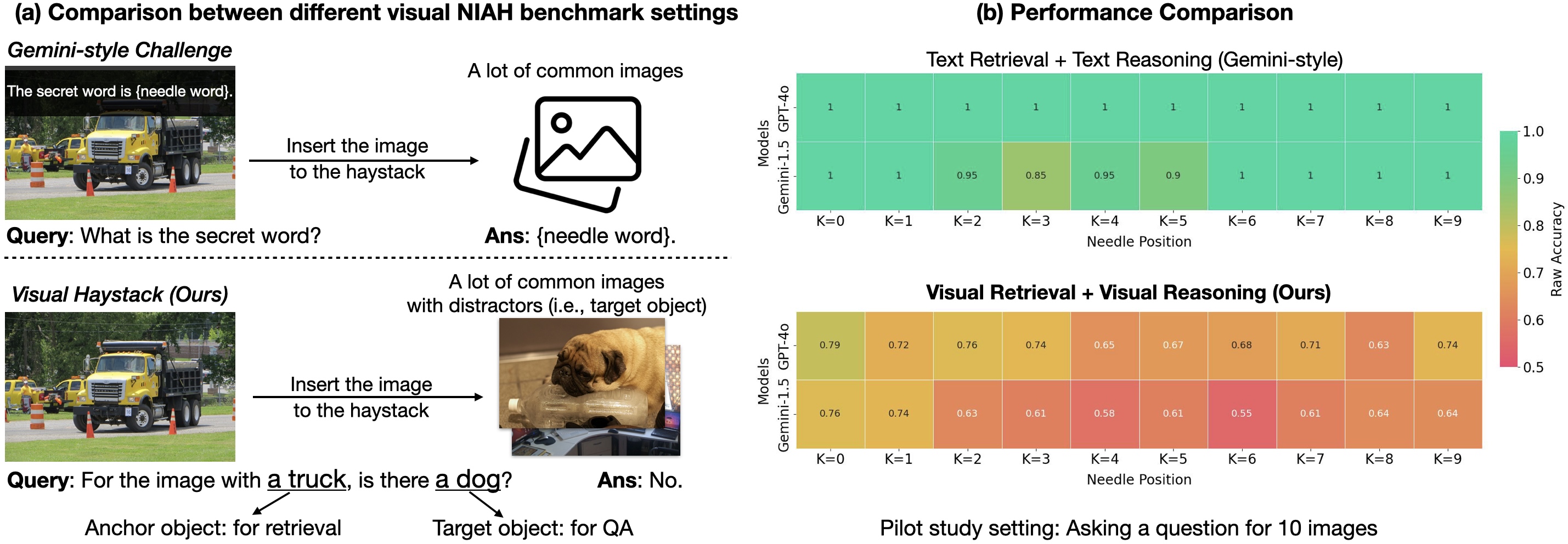
Mean, Median, Mode Term What It Means Why We Need It Real Example Why Not Another Mean Average value To find the center of data Average salary in a company If a few people earn huge salaries (outliers), mean gets unfairly pulled! Median Middle value when data is ordered To find a fair "typical" middle when data has outliers Median house price in a city Median is better when data is uneven (e.g., few very expensive houses) Mode Most common value To find the most frequent happening Most sold shoe size in a store Mode needed when "most common" is more important than "average" ✅ In short: Mean = good for normal data. Median = better when data is skewed (unfair). Mode = for the most popular thing. Range, Variance, Standard Deviation Term What It Means Why We Need It Real Example Why Not Another Range Max - Min value Quick idea of spread Highest and lowest test marks in a class Only shows extremes, not how all values behave Variance Average of squared differences from mean Measure how spread out all data is Variance of stock prices Hard to interpret because it's squared units Standard Deviation Square root of variance Easy-to-read spread measure (same unit as data) How much daily temperatures change from average Easier to explain to non-math people ✅ In short: Range is rough and fast. Variance is deep but harder to read. Standard Deviation is what we usually tell people. Correlation and Covariance Term What It Means Why We Need It Real Example Why Not Another Correlation Strength and direction of relationship between two variables (scale: -1 to 1) Find if two things move together Height vs Weight; Study hours vs Exam score Shows strength and direction both Covariance Direction of relationship, but scale is not fixed Early step before correlation Stock A and Stock B moving up/down together Hard to compare across different datasets ✅ In short: Use Correlation when you want to see if two things are linked. Covariance is more technical, and only used internally.
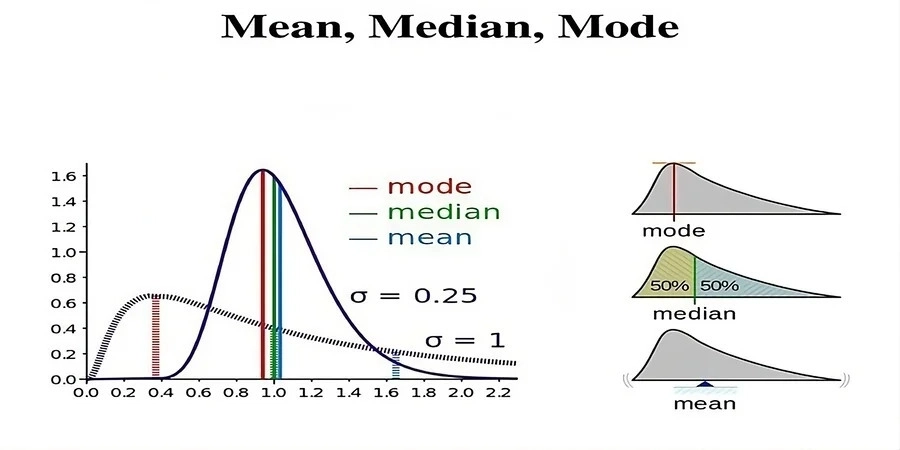
Mean, Median, Mode
| Term | What It Means | Why We Need It | Real Example | Why Not Another |
|---|---|---|---|---|
| Mean | Average value | To find the center of data | Average salary in a company | If a few people earn huge salaries (outliers), mean gets unfairly pulled! |
| Median | Middle value when data is ordered | To find a fair "typical" middle when data has outliers | Median house price in a city | Median is better when data is uneven (e.g., few very expensive houses) |
| Mode | Most common value | To find the most frequent happening | Most sold shoe size in a store | Mode needed when "most common" is more important than "average" |
✅ In short:
Mean = good for normal data.
Median = better when data is skewed (unfair).
Mode = for the most popular thing.
Range, Variance, Standard Deviation
| Term | What It Means | Why We Need It | Real Example | Why Not Another |
|---|---|---|---|---|
| Range | Max - Min value | Quick idea of spread | Highest and lowest test marks in a class | Only shows extremes, not how all values behave |
| Variance | Average of squared differences from mean | Measure how spread out all data is | Variance of stock prices | Hard to interpret because it's squared units |
| Standard Deviation | Square root of variance | Easy-to-read spread measure (same unit as data) | How much daily temperatures change from average | Easier to explain to non-math people |
✅ In short:
- Range is rough and fast.
- Variance is deep but harder to read.
- Standard Deviation is what we usually tell people.
Correlation and Covariance
| Term | What It Means | Why We Need It | Real Example | Why Not Another |
|---|---|---|---|---|
| Correlation | Strength and direction of relationship between two variables (scale: -1 to 1) | Find if two things move together | Height vs Weight; Study hours vs Exam score | Shows strength and direction both |
| Covariance | Direction of relationship, but scale is not fixed | Early step before correlation | Stock A and Stock B moving up/down together | Hard to compare across different datasets |
✅ In short:
- Use Correlation when you want to see if two things are linked.
- Covariance is more technical, and only used internally.





































































































































































![[The AI Show Episode 146]: Rise of “AI-First” Companies, AI Job Disruption, GPT-4o Update Gets Rolled Back, How Big Consulting Firms Use AI, and Meta AI App](https://www.marketingaiinstitute.com/hubfs/ep%20146%20cover.png)








































































































![Ditching a Microsoft Job to Enter Startup Hell with Lonewolf Engineer Sam Crombie [Podcast #171]](https://cdn.hashnode.com/res/hashnode/image/upload/v1746753508177/0cd57f66-fdb0-4972-b285-1443a7db39fc.png?#)




















































.jpg?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)




















































-Nintendo-Switch-2-Hands-On-Preview-Mario-Kart-World-Impressions-&-More!-00-10-30.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)









































































































-xl.jpg)



























![New iPad 11 (A16) On Sale for Just $277.78! [Lowest Price Ever]](https://www.iclarified.com/images/news/97273/97273/97273-640.jpg)

![Apple Foldable iPhone to Feature New Display Tech, 19% Thinner Panel [Rumor]](https://www.iclarified.com/images/news/97271/97271/97271-640.jpg)




































































![[Weekly funding roundup May 3-9] VC inflow into Indian startups touches new high](https://images.yourstory.com/cs/2/220356402d6d11e9aa979329348d4c3e/WeeklyFundingRoundupNewLogo1-1739546168054.jpg)