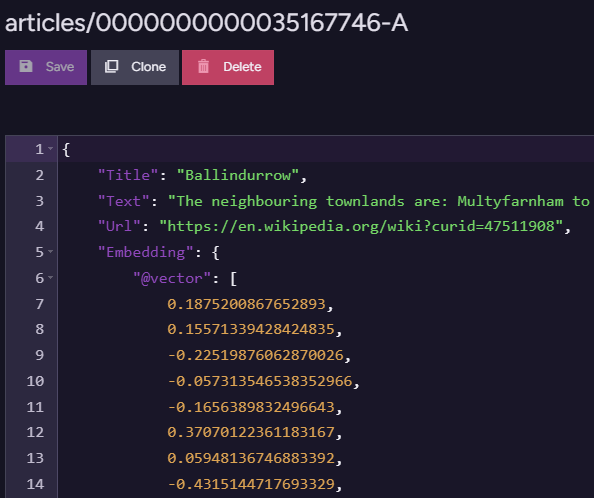
Time Series Forecasting Made Simple (Part 2): Customizing Baseline Models

From simple averages to blended strategies, this part builds a foundation for better forecasting models. The post Time Series Forecasting Made Simple (Part 2): Customizing Baseline Models appeared first on Towards Data Science.

May 9, 2025 - 21:17

Time Series Forecasting Made Simple (Part 2): Customizing Baseline Models

Thank you for the kind response to Part 1, it’s been encouraging to see so many readers interested in time series forecasting.

In Part 1 of this series, we broke down time series data into trend, seasonality, and noise, discussed when to use additive versus multiplicative models, and built a Seasonal Naive baseline forecast using Daily Temperature Data. We evaluated its performance using MAPE (Mean Absolute Percentage Error), which came out to 28.23%.

While the Seasonal Naive model captured the broad seasonal pattern, we also saw that it may not be the best fit for this dataset, as it doesn’t account for subtle shifts in seasonality or long-term trends. This highlights the need to go beyond basic baselines and customize forecasting models to better reflect the underlying data for improved accuracy.

When we applied the Seasonal Naive baseline model, we didn’t account for the trend or use any mathematical formulas, we simply predicted each value based on the same day from the previous year.

First, let’s take a look at the table below, which outlines some common baseline models and when to use each one.

**Table:** Common baseline forecasting models, their descriptions, and when to use each based on data patterns.

These are some of the most commonly used baseline models across various industries.

But what if the data shows both trend and seasonality? In such cases, these simple baseline models might not be enough. As we saw in Part 1, the Seasonal Naive model struggled to fully capture the patterns in the data, resulting in a MAPE of 28.23%.

So, should we jump straight to ARIMA or another complex forecasting model?

Not necessarily.

Before reaching for advanced tools, we can first build our baseline model based on the structure of the data. This helps us build a stronger benchmark — and often, it’s enough to decide whether a more sophisticated model is even needed.

Now that we have examined the structure of the data, which clearly includes both trend and seasonality, we can build a baseline model that takes both components into account.

In Part 1, we used the seasonal decompose method in Python to visualize the trend and seasonality in our data. Now, we’ll take this a step further by actually extracting the trend and seasonal components from that decomposition and using them to build a baseline forecast.

Decomposition of daily temperatures showing trend, seasonal cycles and random fluctuations.

But before we get started, let’s see how the seasonal decompose method figures out the trend and seasonality in our data.

Before using the built-in function, let’s take a small sample from our temperature data and manually go through how the seasonal_decompose method separates trend, seasonality and residuals.

This will help us understand what’s really happening behind the scenes.

Here, we consider a 14-day sample from the temperature dataset to better understand how decomposition works step by step.

We already know that this dataset follows an additive structure, which means each observed value is made up of three parts:

Observed Value = Trend + Seasonality + Residual.

First, let’s look at how the trend is calculated for this sample.
We’ll use a 3-day centered moving average, which means each value is averaged with its immediate neighbor on both sides. This helps smooth out day-to-day variations in the data.

For example, to calculate the trend for February 1, 1981:
Trend = (20.7 + 17.9 + 18.8) / 3
= 19.13

This way, we calculate the trend component for all 14 days in the sample.

Here’s the table showing the 3-day centered moving average trend values for each day in our 14-day sample.

As we can see, the trend values for the first and last dates are ‘NaN’ because there aren’t enough neighboring values to calculate a centered average at those points.

We’ll revisit those missing values once we finish computing the seasonality and residual components.

Before we dive into seasonality, there’s something we said earlier that we should come back to. We mentioned that using a 3-day centered moving average helps in smoothing out day to day variations in the data — but what does that really mean?
Let’s look at a quick example to make it clearer.

We’ve already discussed that the trend reflects the overall direction the data is moving in.

Temperatures are generally higher in summer and lower in winter, that’s the broad seasonal pattern we expect.

But even within summer, temperatures don’t stay exactly the same every day. Some days might be slightly cooler or warmer than others. These are natural daily fluctuations, not signs of sudden climate shifts.

The moving average helps us smooth out these short-term ups and downs so we can focus on the bigger picture, the underlying trend across time.

Since we’re working with a small sample here, the trend may not stand out clearly just yet.

But if you look at the full decomposition plot above, you can see how the trend captures the overall direction the data is moving in, gradually rising, falling or staying steady over time.

Now that we’ve calculated the trend, it’s time to move on to the next component: seasonality.

We know that in an additive model:
Observed Value = Trend + Seasonality + Residual

To isolate seasonality, we start by subtracting the trend from the observed values:
Observed Value – Trend = Seasonality + Residual

The result is known as the detrended series — a combination of the seasonal pattern and any remaining random noise.

Let’s take January 2, 1981 as an example.

Observed temperature: 17.9°C

Trend: 19.13°C

So, the detrended value is:

Detrended = 17.9 – 19.1 = -1.23

In the same way, we calculate the detrended values for all the dates in our sample.

The table above shows the detrended values for each date in our 14-day sample.

Since we’re working with 14 consecutive days, we’ll assume a weekly seasonality and assign a Day Index (from 1 to 7) to each date based on its position in that 7-day cycle.

Now, to estimate seasonality, we take the average of the detrended values that share the same Day Index.

Let’s calculate the seasonality for January 2, 1981. The Day Index for this date is 2, and the other date in our sample with the same index is January 9, 1981. To estimate the seasonal effect for this index, we take the average of the detrended values from both days. This seasonal effect will then be assigned to every date with Index 2 in our cycle.

for January 2, 1981: Detrended value = -1.2 and
for January 9, 1981: Detrended value = 2.1

Average of both values = (-1.2 + 2.1)/2
= 0.45

So, 0.45 is the estimated seasonality for all dates with Index 2.
We repeat this process for each index to calculate the full set of seasonality components.

Here are the values of seasonality for all the dates and these seasonal values reflect the recurring pattern across the week. For example, days with Index 2 tend to be around 0.45^oC warmer than the trend on average, while days with Index 4 tend to be 1.05^oC cooler.

Note: When we say that days with Index 2 tend to be around +0.45°C warmer than the trend on average, we mean that dates like Jan 2 and Jan 9 tend to be about 0.45°C above their own trend value, not compared to the overall dataset trend, but to the local trend specific to each day.

Now that we’ve calculated the seasonal components for each day, you might notice something interesting: even the dates where the trend (and therefore detrended value) was missing, like the first and last dates in our sample — still received a seasonality value.

This is because seasonality is assigned based on the Day Index, which follows a repeating cycle (like 1 to 7 in our weekly example).
So, if January 1 has a missing trend but shares the same index as, say, January 8, it inherits the same seasonal effect that was calculated using valid data from that index group.

In other words, seasonality doesn’t depend on the availability of trend for that specific day, but rather on the pattern observed across all days with the same position in the cycle.

Now we calculate the residual, based on the additive decomposition structure we know that:
Observed Value = Trend + Seasonality + Residual
…which means:
Residual = Observed Value – Trend – Seasonality

You might be wondering, if the detrended values we used to calculate seasonality already had residuals in them, how can we separate them now? The answer comes from averaging. When we group the detrended values by their seasonal position, like Day Index, the random noise tends to cancel itself out. What we’re left with is the repeating seasonal signal. In small datasets this might not be very noticeable, but in larger datasets, the effect is much more clear. And now, with both trend and seasonality removed, what remains is the residual.

We can observe that residuals are not calculated for the first and last dates, since the trend wasn’t available there due to the centered moving average.

Let’s take a look at the final decomposition table for our 14-day sample. This brings together the observed temperatures, the extracted trend and seasonality components, and the resulting residuals.

Now that we’ve calculated the trend, seasonality, and residuals for our sample, let’s come back to the missing values we mentioned earlier. If you look at the decomposition plot for the full dataset, titled “Decomposition of daily temperatures showing trend, seasonal cycles, and random fluctuations”, you’ll notice that the trend line doesn’t appear right at the beginning of the series. The same applies to residuals. This happens because calculating the trend requires enough data before and after each point, so the first few and last few values don’t have a defined trend. That’s also why we see missing residuals at the edges. But in large datasets, these missing values make up only a small portion and don’t affect the overall interpretation. You can still clearly see the trend and patterns over time. In our small 14-day sample, these gaps feel more noticeable, but in real-world time series data, this is completely normal and expected.

Now that we’ve understood how seasonal_decompose works, let’s take a quick look at the code we used to apply it to the temperature data and extract the trend and seasonality components.

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

# Load the dataset
df = pd.read_csv("minimum daily temperatures data.csv")

# Convert 'Date' to datetime and set as index
df['Date'] = pd.to_datetime(df['Date'], dayfirst=True)
df.set_index('Date', inplace=True)

# Set a regular daily frequency and fill missing values using forward fill
df = df.asfreq('D')
df['Temp'].fillna(method='ffill', inplace=True)

# Decompose the daily series (365-day seasonality for yearly patterns)
decomposition = seasonal_decompose(df['Temp'], model='additive', period=365)

# Plot the decomposed components
decomposition.plot()
plt.suptitle('Decomposition of Daily Minimum Temperatures (Daily)', fontsize=14)
plt.tight_layout()
plt.show()

Let’s focus on this part of the code:

decomposition = seasonal_decompose(df['Temp'], model='additive', period=365)

In this line, we’re telling the function what data to use (df['Temp']), which model to apply (additive), and the seasonal period to consider (365), which matches the yearly cycle in our daily temperature data.

Here, we set period=365 based on the structure of the data. This means the trend is calculated using a 365-day centered moving average, which takes 182 values before and after each point. The seasonality is calculated using a 365-day seasonal index, where all January 1st values across years are grouped and averaged, all January 2nd values are grouped, and so on.

When using seasonal_decompose in Python, we simply provide the period, and the function uses that value to determine how both the trend and seasonality should be calculated.

In our earlier 14-day sample, we used a 3-day centered average just to make the math more understandable — but the underlying logic remains the same.

Now that we’ve explored how seasonal_decompose works and understood how it separates a time series into trend, seasonality, and residuals, we’re ready to build a baseline forecasting model.
This model will be constructed by simply adding the extracted trend and seasonality components, essentially assuming that the residual (or noise) is zero.

Once we generate these baseline forecasts, we’ll evaluate how well they perform by comparing them to the actual observed values using MAPE (Mean Absolute Percentage Error).

Here, we’re ignoring the residuals because we’re building a simple baseline model that serves as a benchmark. The goal is to test whether more advanced algorithms are truly necessary.
We’re primarily interested in seeing how much of the variation in the data can be explained using just the trend and seasonality components.

Now we’ll build a baseline forecast by extracting the trend and seasonality components using Python’s seasonal_decompose.

Code:

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from sklearn.metrics import mean_absolute_percentage_error

# Load the dataset
df = pd.read_csv("/minimum daily temperatures data.csv")

# Convert 'Date' to datetime and set as index
df['Date'] = pd.to_datetime(df['Date'], dayfirst=True)
df.set_index('Date', inplace=True)

# Set a regular daily frequency and fill missing values using forward fill
df = df.asfreq('D')
df['Temp'].fillna(method='ffill', inplace=True)

# Split into training (all years except final) and testing (final year)
train = df[df.index.year < df.index.year.max()]
test = df[df.index.year == df.index.year.max()]

# Decompose training data only
decomposition = seasonal_decompose(train['Temp'], model='additive', period=365)

# Extract components
trend = decomposition.trend
seasonal = decomposition.seasonal

# Use last full year of seasonal values from training to repeat for test
seasonal_values = seasonal[-365:].values
seasonal_test = pd.Series(seasonal_values[:len(test)], index=test.index)

# Extend last valid trend value as constant across the test period
trend_last = trend.dropna().iloc[-1]
trend_test = pd.Series(trend_last, index=test.index)

# Create baseline forecast
baseline_forecast = trend_test + seasonal_test

# Evaluate using MAPE
actual = test['Temp']
mask = actual > 1e-3  # avoid division errors on near-zero values
mape = mean_absolute_percentage_error(actual[mask], baseline_forecast[mask])
print(f"MAPE for Baseline Model on Final Year: {mape:.2%}")

# Plot actual vs. forecast
plt.figure(figsize=(12, 5))
plt.plot(actual.index, actual, label='Actual', linewidth=2)
plt.plot(actual.index, baseline_forecast, label='Baseline Forecast', linestyle='--')
plt.title('Baseline Forecast vs. Actual (Final Year)')
plt.xlabel('Date')
plt.ylabel('Temperature (°C)')
plt.legend()
plt.tight_layout()
plt.show()


MAPE for Baseline Model on Final Year: 21.21%

In the code above, we first split the data by using the first 9 years as the training set and the final year as the test set.

We then applied seasonal_decompose to the training data to extract the trend and seasonality components.

Since the seasonal pattern repeats every year, we took the last 365 seasonal values and applied them to the test period.

For the trend, we assumed it remains constant and used the last observed trend value from the training set across all dates in the test year.

Finally, we added the trend and seasonality components to build the baseline forecast, compared it with the actual values from the test set, and evaluated the model using Mean Absolute Percentage Error (MAPE).

We got a MAPE of 21.21% with our baseline model. In Part 1, the seasonal naive approach gave us 28.23%, so we’ve improved by about 7%.

What we’ve built here is not a custom baseline model — it’s a standard decomposition-based baseline.

Let’s now see how we can come up with our own custom baseline for this temperature data.

Now let’s consider the average of temperatures grouped by each day and using them forecast the temperatures for final year.

You might be wondering how we even come up with that idea for a custom baseline in the first place. Honestly, it starts by simply looking at the data. If we can spot a pattern, like a seasonal trend or something that repeats over time, we can build a simple rule around it.

That’s really what a custom baseline is about — using what we understand from the data to make a reasonable prediction. And often, even small, intuitive ideas can work surprisingly well.

Now let’s use Python to calculate the average temperature for each day of the year.

Code:

# Create a new column 'day_of_year' representing which day (1 to 365) each date falls on
train["day_of_year"] = train.index.dayofyear
test["day_of_year"] = test.index.dayofyear

# Group the training data by 'day_of_year' and calculate the mean temperature for each day (averaged across all years)
daily_avg = train.groupby("day_of_year")["Temp"].mean()

# Use the learned seasonal pattern to forecast test data by mapping test days to the corresponding daily average
day_avg_forecast = test["day_of_year"].map(daily_avg)

# Evaluate the performance of this seasonal baseline forecast using Mean Absolute Percentage Error (MAPE)
mape_day_avg = mean_absolute_percentage_error(test["Temp"], day_avg_forecast)
round(mape_day_avg * 100, 2)

To build this custom baseline, we looked at how the temperature typically behaves on each day of the year, averaging across all the training years. Then, we used those daily averages to make predictions for the test set. It’s a simple way to capture the seasonal pattern that tends to repeat every year.

This custom baseline gave us a MAPE of 21.17%, which shows how well it captures the seasonal trend in the data.

Now, let’s see if we can build another custom baseline that captures patterns in the data more effectively and serves as a stronger benchmark.

Now that we’ve used the day-of-year average method for our first custom baseline, you might start wondering what happens in leap years. If we simply number the days from 1 to 365 and take the average, we could end up misled, especially around February 29.

You might be wondering if a single date really matters. In time series analysis, every moment counts. It may not feel that important right now since we’re working with a simple dataset, but in real-world situations, small details like this can have a big impact. Many industries pay close attention to these patterns, and even a one-day difference can affect decisions. That’s why we’re starting with a simple dataset, to help us understand these ideas clearly before applying them to more complex problems.

Now let’s build a custom baseline using calendar-day averages by looking at how the temperature usually behaves on each (month, day) across years.

It’s a simple way to capture the seasonal rhythm of the year based on the actual calendar.

Code:

# Extract the 'month' and 'day' from the datetime index in both training and test sets
train["month"] = train.index.month
train["day"] = train.index.day
test["month"] = test.index.month
test["day"] = test.index.day


# Group the training data by each (month, day) pair and calculate the average temperature for each calendar day
calendar_day_avg = train.groupby(["month", "day"])["Temp"].mean()


# Forecast test values by mapping each test row's (month, day) to the average from training data
calendar_day_forecast = test.apply(
    lambda row: calendar_day_avg.get((row["month"], row["day"]), np.nan), axis=1
)

# Evaluate the forecast using Mean Absolute Percentage Error (MAPE)
mape_calendar_day = mean_absolute_percentage_error(test["Temp"], calendar_day_forecast)

Using this method, we achieved a MAPE of 21.09%.

Now let’s see if we can combine two methods to build a more refined custom baseline. We have already created a calendar-based month-day average baseline. This time we will blend it with the previous day’s actual temperature. The forecasted value will be based 70 percent on the calendar day average and 30 percent on the previous day’s temperature, creating a more balanced and adaptive prediction.

# Create a column with the previous day's temperature 
df["Prev_Temp"] = df["Temp"].shift(1)

# Add the previous day's temperature to the test set
test["Prev_Temp"] = df.loc[test.index, "Prev_Temp"]

# Create a blended forecast by combining calendar-day average and previous day's temperature
# 70% weight to seasonal calendar-day average, 30% to previous day temperature

blended_forecast = 0.7 * calendar_day_forecast.values + 0.3 * test["Prev_Temp"].values

# Handle missing values by replacing NaNs with the average of calendar-day forecasts
blended_forecast = np.nan_to_num(blended_forecast, nan=np.nanmean(calendar_day_forecast))

# Evaluate the forecast using MAPE
mape_blended = mean_absolute_percentage_error(test["Temp"], blended_forecast)

We can call this a blended custom baseline model. Using this approach, we achieved a MAPE of 18.73%.

Let’s take a moment to summarize what we’ve applied to this dataset so far using a simple table.

In Part 1, we used the seasonal naive method as our baseline. In this blog, we explored how the seasonal_decompose function in Python works and built a baseline model by extracting its trend and seasonality components. We then created our first custom baseline using a simple idea based on the day of the year and later improved it by using calendar day averages. Finally, we built a blended custom baseline by combining the calendar average with the previous day’s temperature, which led to even better forecasting results.

In this blog, we used a simple daily temperature dataset to understand how custom baseline models work. Since it’s a univariate dataset, it contains only a time column and a target variable. However, real-world time series data is often much more complex and typically multivariate, with multiple influencing factors. Before we explore how to build custom baselines for such complex datasets, we need to understand another important decomposition method called STL decomposition. We also need a solid grasp of univariate forecasting models like ARIMA and SARIMA. These models are essential because they form the foundation for understanding and building more advanced multivariate time series models.

In Part 1, I mentioned that we would explore the foundations of ARIMA in this part as well. However, as I’m also learning and wanted to keep things focused and digestible, I wasn’t able to fit everything into one blog. To make the learning process smoother, we’ll take it one topic at a time.

In Part 3, we’ll explore STL decomposition and continue building on what we’ve learned so far.

Dataset and License
The dataset used in this article — “Daily Minimum Temperatures in Melbourne” — is available on Kaggle and is shared under the Community Data License Agreement – Permissive, Version 1.0 (CDLA-Permissive 1.0).
This is an open license that permits commercial use with proper attribution. You can read the full license here.

I hope you found this part helpful and easy to follow.
Thanks for reading and see you in Part 3!

The post Time Series Forecasting Made Simple (Part 2): Customizing Baseline Models appeared first on Towards Data Science.