Conquer the Subarray Sum: Sliding Window vs. Brute Force

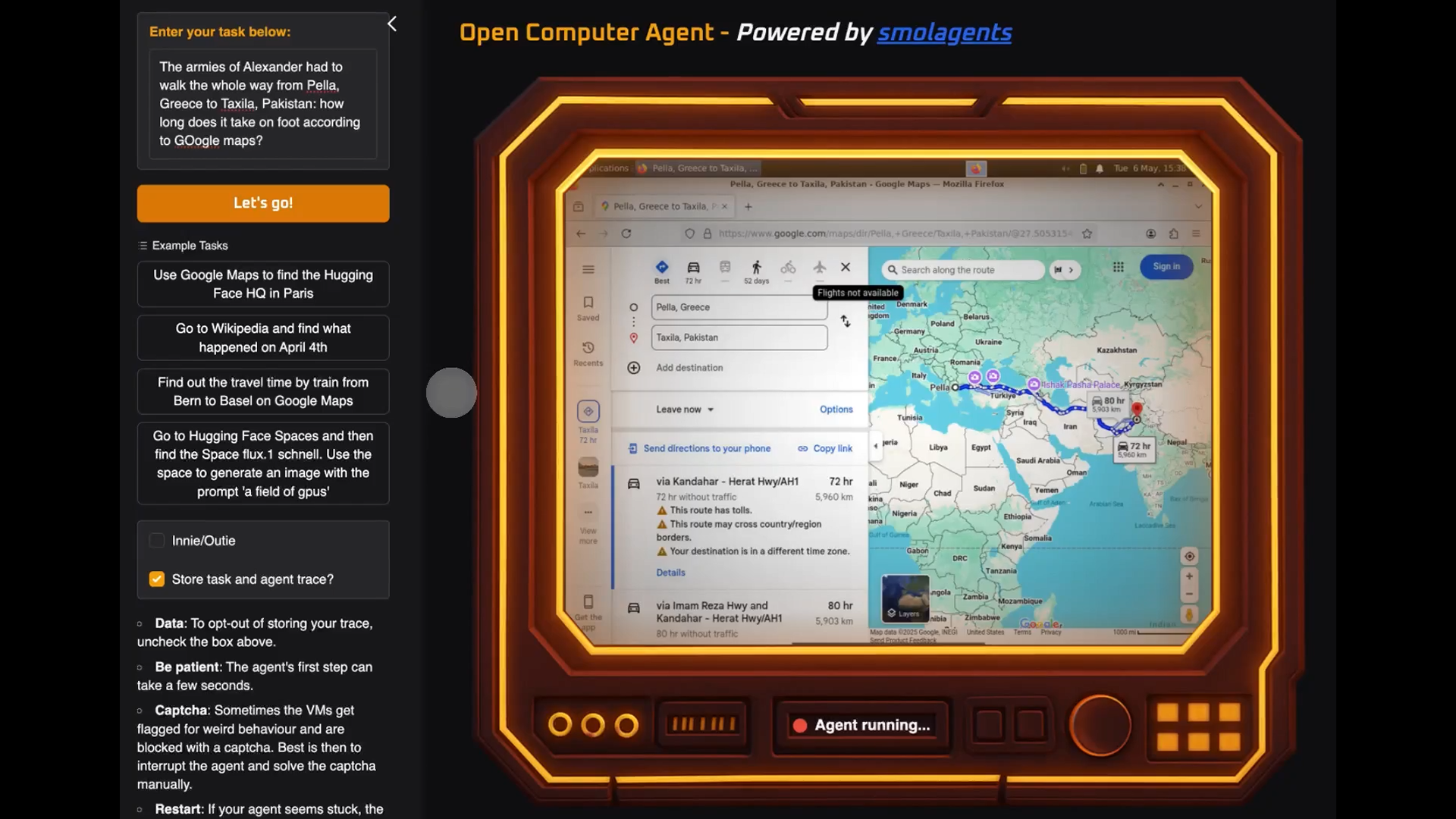
Hello everyone! Ever wrestled with finding the smallest contiguous subarray within an array that sums up to a given target? It's a classic problem, and today we'll explore two contrasting approaches in JavaScript: the elegant sliding window and the straightforward brute force. Let's dive in! The Challenge: Smallest Subarray with Target Sum Given an array of positive integers nums and a target integer target, our mission is to find the smallest contiguous subarray whose elements sum up to be greater than or equal to the target. If no such subarray exists, we return 0 (or some other indicator). The Brute Force Approach: Exhaustive Exploration The most intuitive approach is to consider all possible subarrays. We can achieve this using nested loops: The outer loop iterates through all possible starting indices i from 0 to n-1 (where n is the length of the array). The inner loop iterates through all possible ending indices j from i to n-1. For each subarray nums[i...j], we calculate its sum. If the sum is greater than or equal to the target, we compare its length (j - i + 1) with the current minimum length found so far and update if necessary. function smallestSubarrayBruteForce(nums, target) { const n = nums.length; let minLen = Infinity; for (let i = 0; i

May 9, 2025 - 22:17

Conquer the Subarray Sum: Sliding Window vs. Brute Force

Hello everyone! Ever wrestled with finding the smallest contiguous subarray within an array that sums up to a given target? It's a classic problem, and today we'll explore two contrasting approaches in JavaScript: the elegant sliding window and the straightforward brute force. Let's dive in!

The Challenge: Smallest Subarray with Target Sum

Given an array of positive integers nums and a target integer target, our mission is to find the smallest contiguous subarray whose elements sum up to be greater than or equal to the target. If no such subarray exists, we return 0 (or some other indicator).

The Brute Force Approach: Exhaustive Exploration

The most intuitive approach is to consider all possible subarrays. We can achieve this using nested loops:

The outer loop iterates through all possible starting indices i from 0 to n-1 (where n is the length of the array).
The inner loop iterates through all possible ending indices j from i to n-1.
For each subarray nums[i...j], we calculate its sum.
If the sum is greater than or equal to the target, we compare its length (j - i + 1) with the current minimum length found so far and update if necessary.

function smallestSubarrayBruteForce(nums, target) {
  const n = nums.length;
  let minLen = Infinity;

  for (let i = 0; i < n; i++) {
    let currentSum = 0;
    for (let j = i; j < n; j++) {
      currentSum += nums[j];
      if (currentSum >= target) {
        minLen = Math.min(minLen, j - i + 1);
        break; // Once we find a valid subarray starting at i, we can move to the next i
      }
    }
  }

  return minLen === Infinity ? 0 : minLen;
}

Pros:

Simple to understand and implement. The logic directly mirrors the problem statement.

Cons:

Time Complexity: O(n^2). The nested loops lead to a quadratic time complexity, which can be inefficient for large arrays.
Redundant Calculations: We might recalculate the sum of overlapping subarrays multiple times.

The Sliding Window Technique: Efficiency in Motion

The sliding window technique offers a more optimized solution. Imagine maintaining a "window" defined by two pointers, left and right, that slide across the array.

Initialize left = 0, right = 0, currentSum = 0, and minLen = Infinity.
Expand the window by incrementing right and adding nums[right] to currentSum.
While currentSum is greater than or equal to the target:
- Update minLen = Math.min(minLen, right - left + 1).
- Shrink the window from the left by incrementing left and subtracting nums[left] from currentSum.
Continue expanding the window until right reaches the end of the array.

function smallestSubarraySlidingWindow(nums, target) {
  const n = nums.length;
  let left = 0;
  let currentSum = 0;
  let minLen = Infinity;

  for (let right = 0; right < n; right++) {
    currentSum += nums[right];
    while (currentSum >= target) {
      minLen = Math.min(minLen, right - left + 1);
      currentSum -= nums[left];
      left++;
    }
  }

  return minLen === Infinity ? 0 : minLen;
}

Pros:

Time Complexity: O(n). Each element is visited at most twice (once by the right pointer and once by the left pointer). This linear time complexity makes it significantly faster for larger datasets.
Avoids Redundant Calculations: The currentSum is efficiently updated as the window slides.

Cons:

Can be slightly trickier to grasp initially compared to the brute force approach.

When to Choose Which?

For small input arrays, the simplicity of the brute force approach might be acceptable.
For larger datasets, the sliding window technique is the clear winner due to its superior time complexity. In performance-critical applications, the difference can be substantial.

Conclusion

While the brute force approach provides a straightforward solution, the sliding window technique showcases the power of optimizing algorithms for better efficiency. Happy coding!