A Voyage through Algorithms using Javascript - Quick Sort

What is Quick Sort? Quick Sort is one of the most efficient and widely-used sorting algorithms in computer science. As a "divide and conquer" algorithm, it works by selecting a 'pivot' element and partitioning the array around it. Unlike Merge Sort, which always divides arrays exactly in half, Quick Sort's divisions depend on the chosen pivot. Quick Sort offers average-case time complexity of O(n log n) with in-place sorting capability, requiring only O(log n) additional memory for the recursion stack. However, its performance can degrade to O(n²) in worst-case scenarios, which makes pivot selection strategy important for optimal performance. The tone of this article is assumes you are already familiar with Recursion. If that’s not the case or you need a quick refreshment, I’d suggest you to start from the “A Voyage through Algorithms using Javascript - Recursion” article by following the link below, then come back and continue here later: A Voyage through Algorithms using Javascript - Recursion How Quick Sort Works Quick Sort follows a recursive "divide and conquer" approach with a partitioning twist: Choose: Pick a pivot element from the array (we'll use the last element for simplicity). Partition: Rearrange the array so smaller elements go before the pivot and larger elements go after it. Recursively Sort: Apply Quick Sort to the sub-arrays on both sides of the pivot. Done: Since partitioning puts the pivot in its correct final position, no combining step is needed. Think of Quick Sort like organizing a bookshelf: you pick a reference book (pivot), move all shorter books to its left and taller books to its right, then repeat this process for each section until everything is perfectly organized. The core mechanic lies within how each partition operation brings elements closer to their final positions. Let's visualize this process. The number "4" is the starting target pivot in the example below: Image source: “Quicksort diagram” by Wikipedia user Znupi, released into the public domain. Implementing Quick Sort in JavaScript Let's take a look at the implementation of Quick Sort in JavaScript, with detailed comments explaining each part: function quickSort(arr, start = 0, end = arr.length - 1) { // Base case: if the slice has 1 or 0 items, it's already sorted if (start >= end) { return; } const pivotValue = arr[end]; // Use the last element as pivot let smallerItemsIndex = start; // Marks where smaller values go function swap(array, index1, index2) { [array[index1], array[index2]] = [array[index2], array[index1]]; } // Move smaller elements to the front for (let currentIndex = start; currentIndex = end) return; This means: If there’s nothing to sort (start === end) Or if the subarray is empty (start > end) We just return without doing anything. That’s how the recursion eventually stops: when all the tiny pieces have been handled. Is Quick Sort Stable? No, Quick Sort is not a stable sorting algorithm. Stability in sorting algorithms means that the relative order of equal elements is preserved after sorting. Quick Sort can change the relative positions of equal elements during the partitioning process. Consider this example: if you have an array [3a, 1, 3b, 2] where 3a and 3b have the same value but different origins, Quick Sort might produce [1, 2, 3b, 3a], changing their original relative order. Quick Sort is unstable because during partitioning, elements are moved based on their comparison with the pivot, not their original positions. Elements can be swapped across long distances in the array, potentially crossing over equal elements, and the algorithm prioritizes efficiency over maintaining the relative order of equal elements. When stability matters - like sorting complex objects where secondary sort orders must be preserved, database operations where record order significance exists, or multi-level sorting scenarios - you might want to consider using Merge Sort, which maintains stability while offering O(n log n) performance. Time and Space Complexity Analysis Quick Sort's performance characteristics vary significantly based on pivot selection and input data: Time Complexity: Best Case: O(n log n) - when the pivot consistently divides the array into roughly equal halves Average Case: O(n log n) - for randomly distributed data Worst Case: O(n²) - when the pivot is always the smallest or largest element (like with already sorted arrays) Space Complexity: O(log n) - for the recursion stack in the average case, but can degrade to O(n) in the worst case The key insight is that Quick Sort's performance heavily depends on how well the pivot divides the array. Good pivot selection leads to balanced partitions and optimal performance, while poor pivot selection can cause the algorithm to degrade significantly. Advantages and Disadvantages of Quick Sort Advantages: Exc

Jun 2, 2025 - 00:20

A Voyage through Algorithms using Javascript - Quick Sort

What is Quick Sort?

Quick Sort is one of the most efficient and widely-used sorting algorithms in computer science. As a "divide and conquer" algorithm, it works by selecting a 'pivot' element and partitioning the array around it. Unlike Merge Sort, which always divides arrays exactly in half, Quick Sort's divisions depend on the chosen pivot.

Quick Sort offers average-case time complexity of O(n log n) with in-place sorting capability, requiring only O(log n) additional memory for the recursion stack. However, its performance can degrade to O(n²) in worst-case scenarios, which makes pivot selection strategy important for optimal performance.

The tone of this article is assumes you are already familiar with Recursion. If that’s not the case or you need a quick refreshment, I’d suggest you to start from the “A Voyage through Algorithms using Javascript - Recursion” article by following the link below, then come back and continue here later:

A Voyage through Algorithms using Javascript - Recursion

How Quick Sort Works

Quick Sort follows a recursive "divide and conquer" approach with a partitioning twist:

Choose: Pick a pivot element from the array (we'll use the last element for simplicity).
Partition: Rearrange the array so smaller elements go before the pivot and larger elements go after it.
Recursively Sort: Apply Quick Sort to the sub-arrays on both sides of the pivot.
Done: Since partitioning puts the pivot in its correct final position, no combining step is needed.

Think of Quick Sort like organizing a bookshelf: you pick a reference book (pivot), move all shorter books to its left and taller books to its right, then repeat this process for each section until everything is perfectly organized. The core mechanic lies within how each partition operation brings elements closer to their final positions.

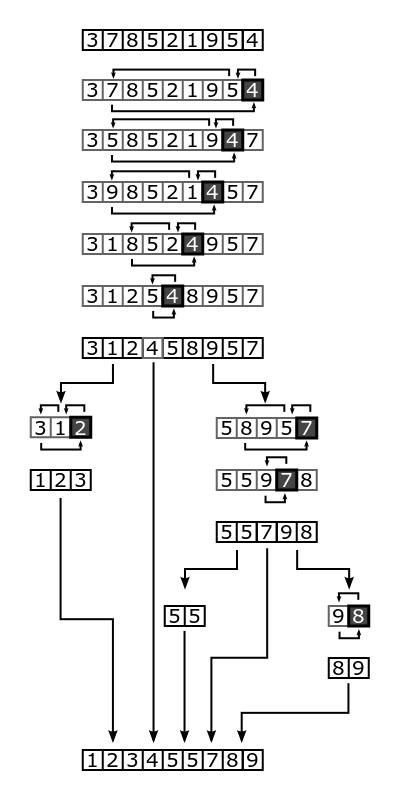
Let's visualize this process. The number "4" is the starting target pivot in the example below:

Image source: “Quicksort diagram” by Wikipedia user Znupi, released into the public domain.

Implementing Quick Sort in JavaScript

Let's take a look at the implementation of Quick Sort in JavaScript, with detailed comments explaining each part:

function quickSort(arr, start = 0, end = arr.length - 1) {
  // Base case: if the slice has 1 or 0 items, it's already sorted
  if (start >= end) {
    return;
  }

  const pivotValue = arr[end]; // Use the last element as pivot
  let smallerItemsIndex = start; // Marks where smaller values go

  function swap(array, index1, index2) {
    [array[index1], array[index2]] = [array[index2], array[index1]];
  }

  // Move smaller elements to the front
  for (let currentIndex = start; currentIndex < end; currentIndex++) {
    if (arr[currentIndex] < pivotValue) {
      swap(arr, currentIndex, smallerItemsIndex);
      smallerItemsIndex++; // Expand the 'less than pivot' zone
    }
  }

  // Place pivot in final position
  swap(arr, smallerItemsIndex, end);

  // Recursive calls to sort left and right of pivot
  quickSort(arr, start, smallerItemsIndex - 1);    // Left side
  quickSort(arr, smallerItemsIndex + 1, end);      // Right side

  return arr;
}

const nums = [99, 44, 6, 2, 1, 5, 63, 87, 283, 4];
const sorted = quickSort(nums);
console.log('Sorted result:', sorted);
// Output: [1, 2, 4, 5, 6, 44, 63, 87, 99, 283]

Key Implementation Details for Quick Sort

Step 1: Creating a Boundary with In-Place Organization

The algorithm works by creating an invisible boundary in the array using the smallerItemsIndex pointer. We're not creating new subarrays - instead, we're organizing elements in-place within the same array. This pointer tracks where the "smaller than pivot" zone ends and acts as a moving boundary that expands as we find more small elements.

At the start, the "boundary" starts at the index zero. And our pivot is the last index value:

// B: Boundary, P: Pivot
[8, 3, 5, 2, 4]
 ^           ^
 B           P

Step 2: Swapping to Maintain the Boundary

As we scan through the array, whenever we find an element smaller than our pivot, we swap it with the element at our boundary position and move the boundary forward. This swap operation keeps all smaller elements on the left side of our invisible boundary line. In this example, we use the Lomuto partitioning method rather than the Hoare partition scheme because it's simpler for understanding Quick sort since it always uses the last element as the pivot.

In real-world applications, pivot selection can greatly affect performance. Choosing a poor pivot (like always picking the first or last element on a nearly sorted list) can lead to much slower runtimes.

Example of boundary movement:

Pick pivot: 4
Boundary starts at index 0
Iteration begins at index 0

Scan:

8 > 4 → skip

// B: Boundary, P: Pivot, I: Iterator
[8, 3, 5, 2, 4]
 ^           ^
 B           P
 I

3 < 4 → swap with index 0 (8) → [3, 8, 5, 2, 4], move boundary → 1

// B: Boundary, P: Pivot, I: Iterator
[3, 8, 5, 2, 4]
    ^        ^
    B        P
    I

5 > 4 → skip

// B: Boundary, P: Pivot, I: Iterator
[3, 8, 5, 2, 4]
    ^  ^     ^
    B  I     P

2 < 4 → swap with index 1 → [3, 2, 5, 8, 4], move boundary → 2

// B: Boundary, P: Pivot, I: Iterator
[3, 2, 5, 8, 4]
       ^  ^  ^
       B  I  P

Now finally, swap the pivot 4 into the boundary index → [3, 2, 4, 8, 5]

// B: Boundary, P: Pivot, I: Iterator
[3, 2, 4, 8, 5]
       ^     ^
     P & B   I

Pivot 4 is now where it belongs.

Step 3: Pivot Is Placed, Time for Recursion

As we've seen, the pivot is now in its correct position (swapped into the boundary spot). Now comes the recursive step:

Everything to the left is smaller
Everything to the right is larger
The pivot is exactly where it belongs and locked in.

At this point, we don’t touch the pivot anymore. Instead, we make two recursive calls:

One for the left side of the pivot
One for the right side

We only send the parts excluding the pivot, because it’s already in the correct position.

After placing 4, our array looks like this:

[3, 2, 4, 8, 5]
       ^
     Pivot

Now we call Quick Sort again on:
Left side: [3, 2]
Right side: [8, 5]

Each of these subarrays will go through the same process:

Pick a pivot
Partition the section
Lock the pivot
Recurse again

Eventually, every element gets locked into place, one pivot at a time. When all recursive calls finish, the array is fully sorted - and we didn’t need any extra arrays to do it.

Step 4: When Does the Recursion Stop?

Like any recursive function, Quick Sort needs a condition to stop calling itself. That’s called the base case.

We stop recursing when the slice of the array we’re working on has zero or one element - because that’s already sorted by definition.

In code, it usually looks something like this:

if (start >= end) return;

This means:

If there’s nothing to sort (start === end)
Or if the subarray is empty (start > end)

We just return without doing anything. That’s how the recursion eventually stops: when all the tiny pieces have been handled.

Is Quick Sort Stable?

No, Quick Sort is not a stable sorting algorithm. Stability in sorting algorithms means that the relative order of equal elements is preserved after sorting. Quick Sort can change the relative positions of equal elements during the partitioning process.

Consider this example: if you have an array [3a, 1, 3b, 2] where 3a and 3b have the same value but different origins, Quick Sort might produce [1, 2, 3b, 3a], changing their original relative order.

Quick Sort is unstable because during partitioning, elements are moved based on their comparison with the pivot, not their original positions. Elements can be swapped across long distances in the array, potentially crossing over equal elements, and the algorithm prioritizes efficiency over maintaining the relative order of equal elements.

When stability matters - like sorting complex objects where secondary sort orders must be preserved, database operations where record order significance exists, or multi-level sorting scenarios - you might want to consider using Merge Sort, which maintains stability while offering O(n log n) performance.

Time and Space Complexity Analysis

Quick Sort's performance characteristics vary significantly based on pivot selection and input data:

Time Complexity:
- Best Case: O(n log n) - when the pivot consistently divides the array into roughly equal halves
- Average Case: O(n log n) - for randomly distributed data
- Worst Case: O(n²) - when the pivot is always the smallest or largest element (like with already sorted arrays)
Space Complexity: O(log n) - for the recursion stack in the average case, but can degrade to O(n) in the worst case

The key insight is that Quick Sort's performance heavily depends on how well the pivot divides the array. Good pivot selection leads to balanced partitions and optimal performance, while poor pivot selection can cause the algorithm to degrade significantly.

Advantages and Disadvantages of Quick Sort

Advantages:

Excellent average-case performance of O(n log n)
In-place sorting with minimal memory overhead
Cache-efficient due to good locality of reference
Widely implemented in standard libraries
Generally faster than Merge Sort for in-memory sorting
Easily parallelizable

Disadvantages:

Unstable sorting algorithm (doesn't preserve relative order of equal elements)
Worst-case time complexity of O(n²)
Performance varies significantly with input data and pivot selection
Not suitable for scenarios requiring guaranteed O(n log n) performance
Can cause stack overflow on very large inputs due to deep recursion

When to Use Quick Sort

General-purpose sorting: When you need efficient sorting for most datasets
Memory-constrained environments: Where in-place sorting is valuable
Performance-critical applications: Where average-case performance matters more than worst-case guarantees
Large datasets: Where cache-friendly behavior provides benefits
When stability isn't required: Perfect for scenarios where maintaining relative order of equal elements doesn't matter

When NOT to Use Quick Sort

When you need guaranteed O(n log n) performance (use Merge Sort instead)
When sorting stability is required
For small arrays (simple algorithms like Insertion Sort might be more efficient)
In adversarial environments where worst-case performance could be exploited

Practical Applications and Use Cases

Many programming languages use optimized versions of Quick Sort in their built-in sorting functions. Database systems employ it for sorting intermediate results during query execution, and operating systems use it for file system operations like directory listings. In graphics programming, it's commonly used for sorting objects by depth for rendering operations. Data analytics platforms leverage Quick Sort for processing large datasets where average-case performance is more important than worst-case guarantees, and gaming applications use it for sorting game objects, leaderboards, and real-time data where performance is critical.

Conclusion

Quick Sort is a classic example of the “divide and conquer” strategy in action. It stands out for its efficiency and in-place sorting, especially when memory is limited and average-case performance matters.

That said, it’s not always the safest pick. Its worst-case performance and lack of stability can be dealbreakers in certain cases. But if you understand how it works, particularly how partitioning and pivot placement drive the recursion - you’ll not only be able to implement it confidently, but also gain a deeper understanding of algorithm design in general.