Dev.to

3272. Find the Count of Good Integers

3272. Find the Count of Good Integers Difficulty: Hard Topics: Hash Table, Math, Combinatorics, Enumeration You are given two positive integers n and k. An integer x is called k-palindromic if: x is a palindrome1. x is divisible by k. An integer is called good if its digits can be rearranged to form a k-palindromic integer. For example, for k = 2, 2020 can be rearranged to form the k-palindromic integer 2002, whereas 1010 cannot be rearranged to form a k-palindromic integer. Return the count of good integers containing n digits. Note that any integer must not have leading zeros, neither before nor after rearrangement. For example, 1010 cannot be rearranged to form 101. Example 1: Input: n = 3, k = 5 Output: 27 Explanation: Some of the good integers are: 551 because it can be rearranged to form 515. 525 because it is already k-palindromic. Example 2: Input: n = 1, k = 4 Output: 2 Explanation: The two good integers are 4 and 8. Example 3: Input: n = 5, k = 6 Output: 2468 Constraints: 1

Apr 12, 2025 - 14:53

Difficulty: Hard

Topics: Hash Table, Math, Combinatorics, Enumeration

You are given two positive integers n and k.

An integer x is called k-palindromic if:

x is a palindrome¹.
x is divisible by k.

An integer is called good if its digits can be rearranged to form a k-palindromic integer. For example, for k = 2, 2020 can be rearranged to form the k-palindromic integer 2002, whereas 1010 cannot be rearranged to form a k-palindromic integer.

Return the count of good integers containing n digits.

Note that any integer must not have leading zeros, neither before nor after rearrangement. For example, 1010 cannot be rearranged to form 101.

Example 1:

Input: n = 3, k = 5
Output: 27
Explanation: Some of the good integers are:
- 551 because it can be rearranged to form 515.
- 525 because it is already k-palindromic.

Example 2:

Input: n = 1, k = 4
Output: 2
Explanation: The two good integers are 4 and 8.

Example 3:

Input: n = 5, k = 6
Output: 2468

Constraints:

1 <= n <= 10
1 <= k <= 9

Hint:

How to generate all K-palindromic strings of length n? Do we need to go through all n digits?
Use permutations to calculate the number of possible rearrangements.

Solution:

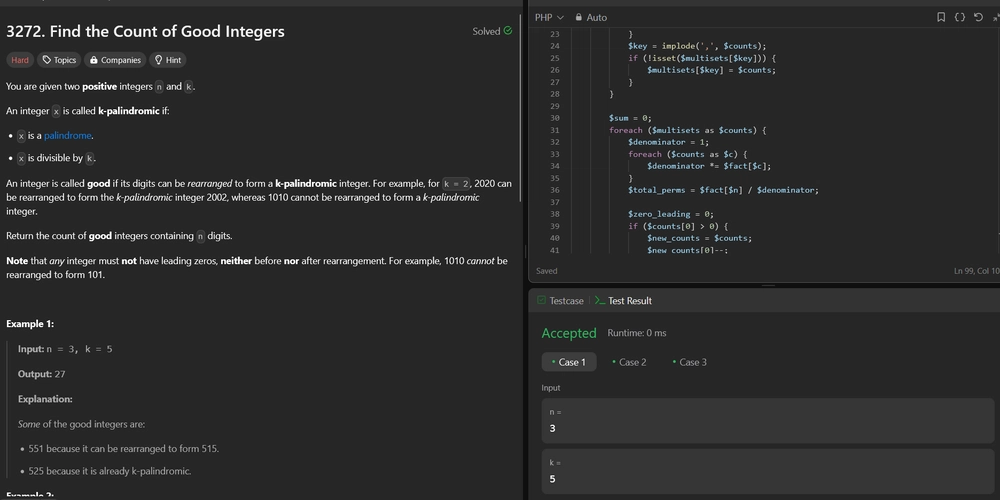
We need to count the number of n-digit integers (called good integers) that can be rearranged into a k-palindromic integer. A k-palindromic integer is a palindrome that is divisible by k. The solution involves generating all possible palindromes of length n, checking their divisibility by k, and then counting the valid permutations of their digits that do not have leading zeros.

Approach

Generate Palindromes: Generate all possible palindromes of length n. For even n, generate the first half and mirror it. For odd n, generate the first half, middle digit, and mirror the first half. Special handling is required for n=1.
Check Divisibility: For each generated palindrome, check if it is divisible by k.
Collect Digit Multisets: For each valid palindrome, collect the digit counts (multiset) to track unique combinations.
Calculate Valid Permutations: For each unique multiset, calculate the number of valid permutations (n-digit numbers without leading zeros).

Let's implement this solution in PHP: 3272. Find the Count of Good Integers


/**
 * @param Integer $n
 * @param Integer $k
 * @return Integer
 */
function countGoodIntegers($n, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * @param $n
 * @param $k
 * @return array
 */
function generatePalindromes($n, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example usage:
echo countGoodIntegers(3, 5) . "\n"; // Output: 27
echo countGoodIntegers(1, 4) . "\n"; // Output: 2
echo countGoodIntegers(5, 6) . "\n"; // Output: 2468
?>

Explanation:

Generating Palindromes: The function generatePalindromes creates all possible palindromes of length n. For even n, it generates the first half and mirrors it. For odd n, it generates the first half, adds a middle digit, and mirrors the first half. Special handling for n=1 ensures only valid single-digit numbers are considered.
Digit Multisets: Each palindrome's digit counts are stored to avoid duplicates. This helps in efficiently counting permutations later.
Valid Permutations Calculation: For each unique multiset, the number of valid permutations (excluding those with leading zeros) is calculated using factorial-based combinatorial formulas. This ensures we count only valid n-digit numbers.

This approach efficiently combines palindrome generation, divisibility checks, and combinatorial counting to solve the problem within the constraints.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks