Dev.to

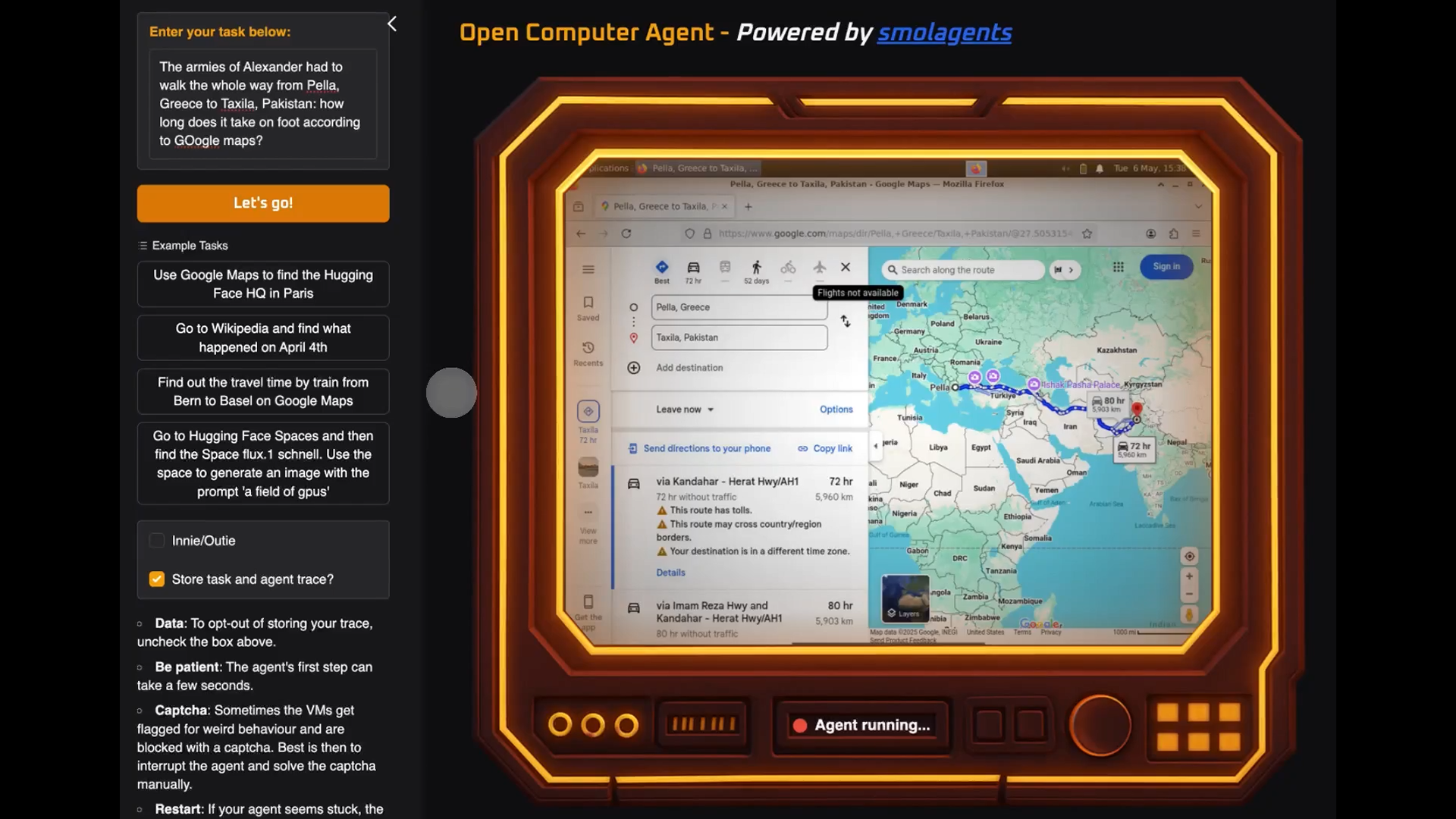
How can I optimize a Go solution for maximum score problem?

Introduction In this article, we will dive into an efficient Go solution for the problem of finding the maximum score from two sorted arrays. This problem can often be found on competitive programming platforms, including LeetCode. We'll discuss the approach of using two pointers to solve the problem efficiently. Additionally, we will explore some optimizations that you can implement to ensure your code handles large inputs without facing overflow issues. Why Do Overflow Issues Occur? When working with large datasets, especially in programming languages like Go, it’s crucial to choose the right variable types. In the context of this problem, overflowing can happen if the computed sums exceed the limits of the data type used. Here, we are already using int64, which should be sufficient for storing large values, but you might still encounter issues depending on how variables are handled during summation. The Approach The core idea of the solution involves traversing two arrays simultaneously. Here's a step-by-step breakdown of how to implement this in Go: Step 1: Function to Get Maximum Let's start with a helper function that returns the maximum of two int64 values. func max(a, b int64) int64 { if a > b { return a } return b } Step 2: Initialize Variables Next, in the main function maxSum, initialize all necessary variables. This includes counters for both arrays and a mod constant to handle large sums. func maxSum(nums1 []int, nums2 []int) int { var cnt1 int64 = 0 var cnt2 int64 = 0 var ans int64 = 0 p1 := 0 p2 := 0 n1 := len(nums1) n2 := len(nums2) const N int64 = 1e9 + 7 } Step 3: Preprocessing To avoid boundary overflow, preprocess both arrays by appending a large value at the end: var _nums1 [100010]int64 var _nums2 [100010]int64 for i:=0; i

May 9, 2025 - 18:23
 0
How can I optimize a Go solution for maximum score problem?

Introduction

In this article, we will dive into an efficient Go solution for the problem of finding the maximum score from two sorted arrays. This problem can often be found on competitive programming platforms, including LeetCode. We'll discuss the approach of using two pointers to solve the problem efficiently. Additionally, we will explore some optimizations that you can implement to ensure your code handles large inputs without facing overflow issues.

Why Do Overflow Issues Occur?

When working with large datasets, especially in programming languages like Go, it’s crucial to choose the right variable types. In the context of this problem, overflowing can happen if the computed sums exceed the limits of the data type used. Here, we are already using int64, which should be sufficient for storing large values, but you might still encounter issues depending on how variables are handled during summation.

The Approach

The core idea of the solution involves traversing two arrays simultaneously. Here's a step-by-step breakdown of how to implement this in Go:

Step 1: Function to Get Maximum

Let's start with a helper function that returns the maximum of two int64 values. 

func max(a, b int64) int64 {
    if a > b {
        return a
    }
    return b
}

Step 2: Initialize Variables

Next, in the main function maxSum, initialize all necessary variables. This includes counters for both arrays and a mod constant to handle large sums. 

func maxSum(nums1 []int, nums2 []int) int {
    var cnt1 int64 = 0
    var cnt2 int64 = 0
    var ans int64 = 0
    p1 := 0
    p2 := 0
    n1 := len(nums1)
    n2 := len(nums2)
    const N int64 = 1e9 + 7
}

Step 3: Preprocessing

To avoid boundary overflow, preprocess both arrays by appending a large value at the end: 

var _nums1 [100010]int64
var _nums2 [100010]int64
for i:=0; i

Step 4: Main Logic

This part of code will implement a loop to traverse both arrays. 

for p1 < n1 || p2 < n2 {
    for _nums1[p1] < _nums2[p2] {
        cnt1 = (cnt1 % N + _nums1[p1] % N) % N
        p1++
    }
    for _nums2[p2] < _nums1[p1] {
        cnt2 = (cnt2 % N + _nums2[p2] % N) % N
        p2++
    }
    if _nums2[p2] == _nums1[p1] {
        ans = (ans % N + max(cnt1, cnt2) % N) % N
        cnt1 = 0
        cnt2 = 0
        if p2 < n2 {
            ans = (ans % N + _nums2[p2] % N) % N
        }
        if p1 < n1 {
            p1++
        }
        if p2 < n2 {
            p2++
        }
    }
}

Step 5: Return Result

Finally, return the computed maximum score as follows: 

return int(ans)
}

Conclusion

By implementing this two-pointer solution, we can efficiently solve the maximum score problem with large input arrays. The use of int64 for our sum calculations ensures that we can handle vast sums without encountering integer overflow. If you face any unexpected results during testing, double-check your implementation against edge cases, such as arrays with no common elements or varying lengths.

Frequently Asked Questions

What happens if two large arrays cause overflow?

Using int64 should normally be sufficient unless you are summing a large number of elements. Ensure calculations are properly modulo reduced to avoid reaching the maximum limit.

What's the time complexity of this algorithm?

The time complexity is O(n + m) where n and m are the lengths of the two arrays, as we traverse each array only once.

Can this approach handle different data types?

This solution is tailored for int arrays, but you can modify it to handle other numeric types if needed, keeping in mind their respective limits.

This implementation passed 80 out of 82 test cases on LeetCode, indicating that while mostly efficient, there may be edge cases to consider when working with large inputs. Test carefully!

Read More

Tags:

Previous Article

Sharding vs. Partitioning

Next Article

What is a Large Language Model (LLM)? A Comprehensive Guide for Developers

Related Posts

Nice article!

Nice article!

May 6, 2025  0

Implementing HTMX with Flask and Jinja2 for Dynamic Content Rendering

Implementing HTMX with Flask and Jinja2 for Dynamic Con...

May 3, 2025  0

Day 152/365 [Learning Full stack]

Day 152/365 [Learning Full stack]

May 1, 2025  0