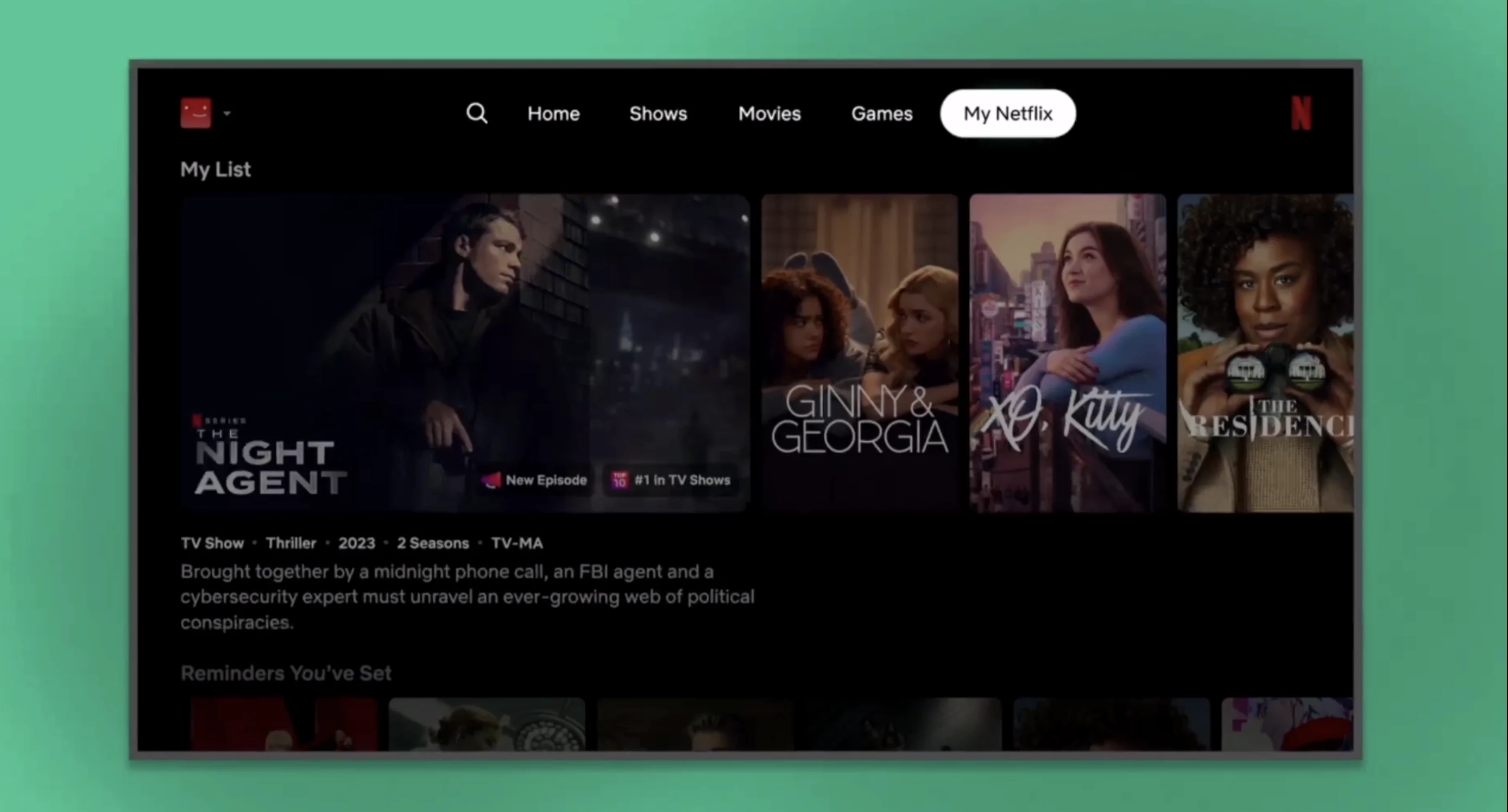
3341. Find Minimum Time to Reach Last Room I

3341. Find Minimum Time to Reach Last Room I Difficulty: Medium Topics: Array, Graph, Heap (Priority Queue), Matrix, Shortest Path There is a dungeon with n x m rooms arranged as a grid. You are given a 2D array moveTime of size n x m, where moveTime[i][j] represents the minimum time in seconds when you can start moving to that room. You start from the room (0, 0) at time t = 0 and can move to an adjacent room. Moving between adjacent rooms takes exactly one second. Return the minimum time to reach the room (n - 1, m - 1). Two rooms are adjacent if they share a common wall, either horizontally or vertically. Example 1: Input: moveTime = [[0,4],[4,4]] Output: 6 Explanation: The minimum time required is 6 seconds. At time t == 4, move from room (0, 0) to room (1, 0) in one second. At time t == 5, move from room (1, 0) to room (1, 1) in one second. Example 2: Input: moveTime = [[0,0,0],[0,0,0]] Output: 3 Explanation: The minimum time required is 3 seconds. At time t == 0, move from room (0, 0) to room (1, 0) in one second. At time t == 1, move from room (1, 0) to room (1, 1) in one second. At time t == 2, move from room (1, 1) to room (1, 2) in one second. Example 3: Input: moveTime = [[0,1],[1,2]] Output: 3 Constraints: 2 Explanation: Initialization: The distance array dist is initialized to infinity (PHP_INT_MAX) except for the starting room (0,0) which is set to 0. This array keeps track of the minimum time to reach each room. Priority Queue: The priority queue is initialized with the starting room and time 0. The queue processes rooms in ascending order of their arrival times using a min-heap (simulated with negative priorities in PHP). Processing Rooms: For each room dequeued, check if it is the destination. If so, return the current time. Otherwise, explore all adjacent rooms, compute the new arrival time considering the room's minimum time requirement, and update the distance array if a shorter path is found. Adjacent Rooms Check: For each valid adjacent room, the new arrival time is calculated as the maximum of the current time and the room's minimum time requirement plus one second. This ensures that we respect the minimum time requirement for entering each room. This approach efficiently finds the shortest path using Dijkstra's algorithm, ensuring that we always explore the shortest path first and update our distances accordingly. The solution handles all edge cases and constraints effectively. Contact Links If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks

May 7, 2025 - 02:43

Difficulty: Medium

Topics: Array, Graph, Heap (Priority Queue), Matrix, Shortest Path

There is a dungeon with n x m rooms arranged as a grid.

You are given a 2D array moveTime of size n x m, where moveTime[i][j] represents the minimum time in seconds when you can start moving to that room. You start from the room (0, 0) at time t = 0 and can move to an adjacent room. Moving between adjacent rooms takes exactly one second.

Return the minimum time to reach the room (n - 1, m - 1).

Two rooms are adjacent if they share a common wall, either horizontally or vertically.

Example 1:

Input: moveTime = [[0,4],[4,4]]
Output: 6
Explanation: The minimum time required is 6 seconds.
- At time t == 4, move from room (0, 0) to room (1, 0) in one second.
- At time t == 5, move from room (1, 0) to room (1, 1) in one second.

Example 2:

Input: moveTime = [[0,0,0],[0,0,0]]
Output: 3
Explanation: The minimum time required is 3 seconds.
- At time t == 0, move from room (0, 0) to room (1, 0) in one second.
- At time t == 1, move from room (1, 0) to room (1, 1) in one second.
- At time t == 2, move from room (1, 1) to room (1, 2) in one second.

Example 3:

Input: moveTime = [[0,1],[1,2]]
Output: 3

Constraints:

2 <= n == moveTime.length <= 50
2 <= m == moveTime[i].length <= 50
0 <= moveTime[i][j] <= 10⁹

Hint:

Use shortest path algorithms.

Solution:

We need to determine the minimum time required to reach the last room of a dungeon grid starting from the top-left corner (0,0) at time 0. Each room has a minimum time requirement before you can start moving into it, and moving between adjacent rooms takes exactly one second.

Approach

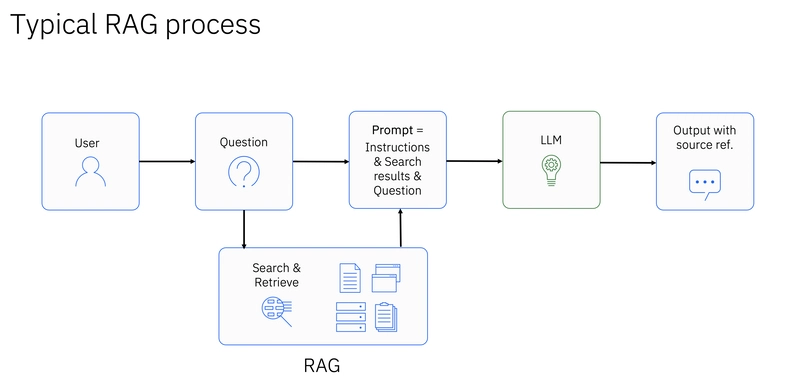
The problem can be efficiently solved using Dijkstra's algorithm, which is typically used to find the shortest path in a graph with non-negative weights. In this context, each room is a node, and the edges between nodes represent the time required to move from one room to another. The key insight is to model the arrival time at each room as the distance in Dijkstra's algorithm, considering both the movement time and the minimum time requirement of each room.

Initialization: Start from the top-left room (0,0) at time 0. Use a priority queue (min-heap) to explore rooms in order of their arrival times.
Priority Queue: Use the priority queue to always process the room with the smallest current arrival time. This ensures that we explore the shortest path first.
Adjacent Rooms: For each room, check all adjacent rooms (up, down, left, right). Calculate the arrival time for each adjacent room as the maximum of the current time and the room's minimum time requirement, plus one second for the move.
Update Distances: If the calculated arrival time for an adjacent room is less than the previously recorded time, update the time and add the room to the priority queue.

Let's implement this solution in PHP: 3341. Find Minimum Time to Reach Last Room I


/**
 * @param Integer[][] $moveTime
 * @return Integer
 */
function minTimeToReach($moveTime) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test Example
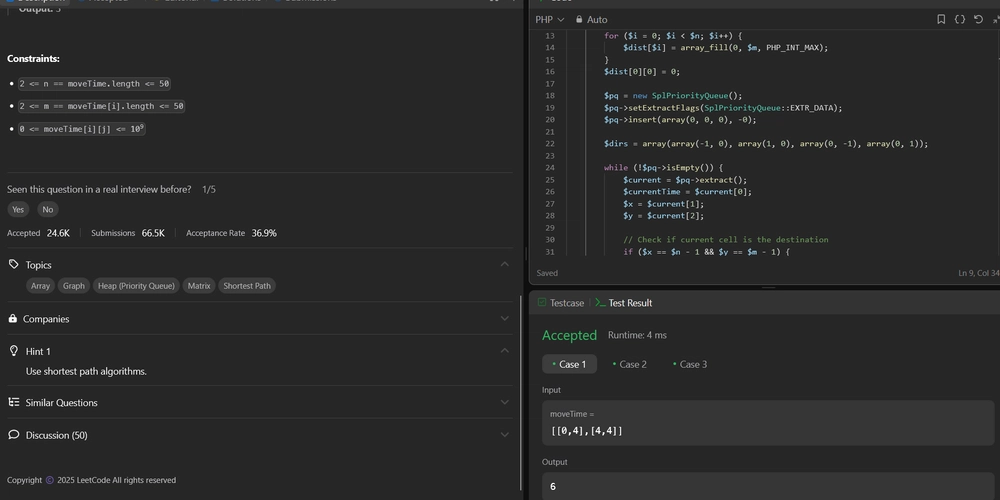
$moveTime1 = [[0, 4], [4, 4]];
$moveTime2 = [[0, 0, 0], [0, 0, 0]];
$moveTime3 = [[0, 1], [1, 2]];

echo minTimeToReach($moveTime1) . "\n"; // 6
echo minTimeToReach($moveTime2) . "\n"; // 3
echo minTimeToReach($moveTime3) . "\n"; // 3
?>

Explanation:

Initialization: The distance array dist is initialized to infinity (PHP_INT_MAX) except for the starting room (0,0) which is set to 0. This array keeps track of the minimum time to reach each room.
Priority Queue: The priority queue is initialized with the starting room and time 0. The queue processes rooms in ascending order of their arrival times using a min-heap (simulated with negative priorities in PHP).
Processing Rooms: For each room dequeued, check if it is the destination. If so, return the current time. Otherwise, explore all adjacent rooms, compute the new arrival time considering the room's minimum time requirement, and update the distance array if a shorter path is found.
Adjacent Rooms Check: For each valid adjacent room, the new arrival time is calculated as the maximum of the current time and the room's minimum time requirement plus one second. This ensures that we respect the minimum time requirement for entering each room.

This approach efficiently finds the shortest path using Dijkstra's algorithm, ensuring that we always explore the shortest path first and update our distances accordingly. The solution handles all edge cases and constraints effectively.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks