Dev.to

Quick Sort

Quicksort is a sorting algorithm that uses the divide and conquer method. 1. First, a pivot element is chosen from the array. 2. The array is then divided into two parts: Elements less than the pivot go to the left. Elements greater than the pivot go to the right. 3. This process is repeated for the left and right parts until each subarray has only one element. 4. At that point, the elements are already sorted, and the final sorted array is formed by combining all the parts. Working of Quicksort Algorithm 1. Choose the Pivot Element In Quicksort, the pivot can be chosen in different ways. In our case, we will always pick the last element of the array as the pivot. 2. Split into Left and Right Arrays Create a left array with elements less than pivot. Create a right array with elements more than pivot. 3. Recursive Calls on Subarrays As we know, JavaScript is synchronous. So, we first call quickSort() recursively on the left array. But as you can see above, the left array has only one element, so it returns immediately. Next, we call quickSort() on the right array and step 1 and 2 will repeat during this process. 4. Again, we recursively call on right array 5. Finally, we combine the returned value. You can understand how the returned values are combined with the help of the visual image below. Quick Sort Algorithm FUNCTION quickSort(arr): IF length of arr

Apr 10, 2025 - 17:37

Quicksort is a sorting algorithm that uses the divide and conquer method.

1. First, a pivot element is chosen from the array.

2. The array is then divided into two parts:

Elements less than the pivot go to the left.
Elements greater than the pivot go to the right.

3. This process is repeated for the left and right parts until each
subarray has only one element.

4. At that point, the elements are already sorted, and the final sorted array is formed by combining all the parts.

Working of Quicksort Algorithm

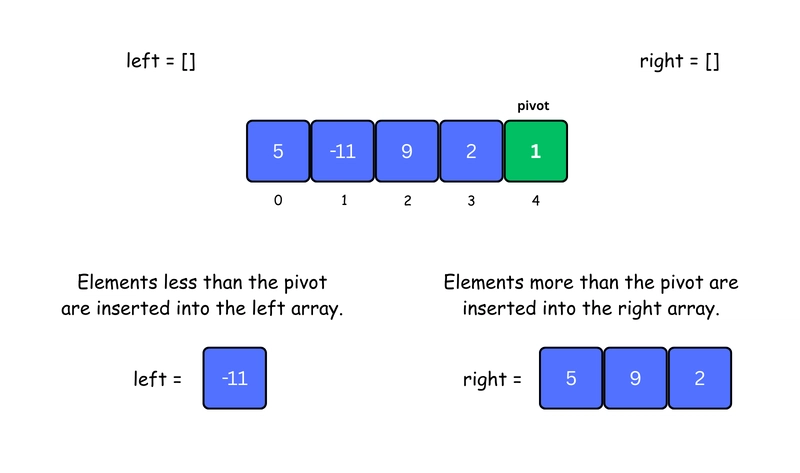
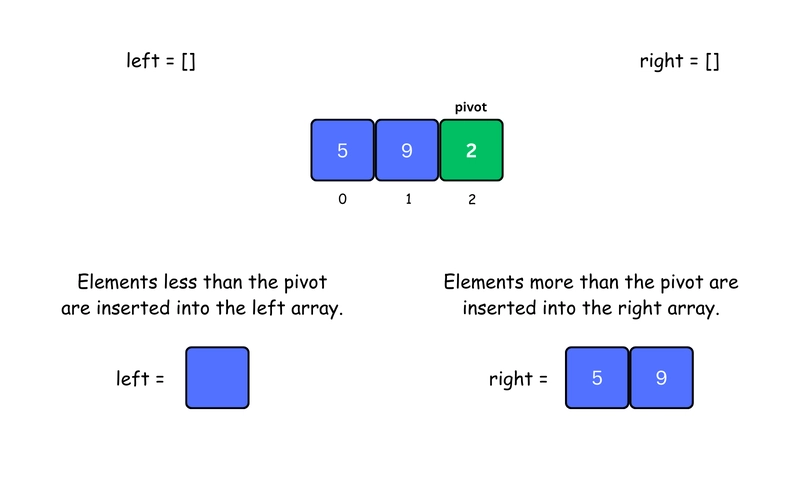
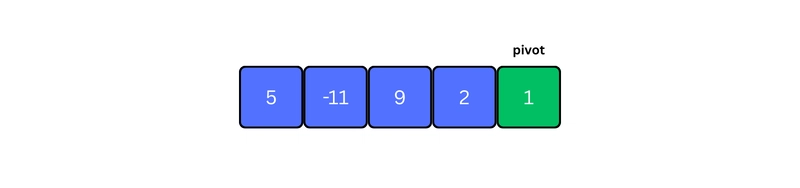
1. Choose the Pivot Element
In Quicksort, the pivot can be chosen in different ways. In our case, we will always pick the last element of the array as the pivot.

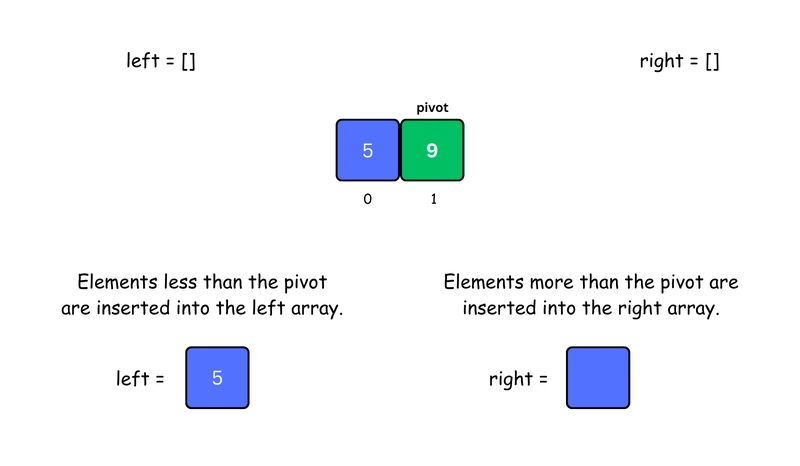
2. Split into Left and Right Arrays

Create a left array with elements less than pivot.
Create a right array with elements more than pivot.

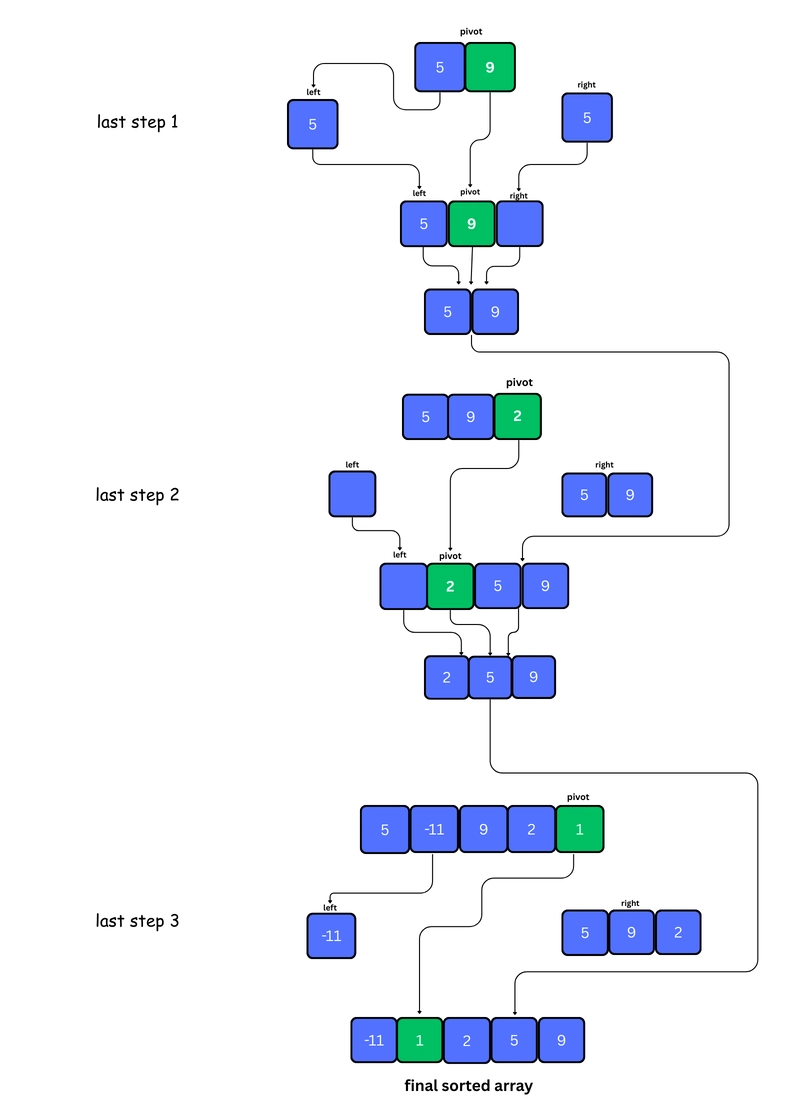
3. Recursive Calls on Subarrays
As we know, JavaScript is synchronous. So, we first call quickSort() recursively on the left array. But as you can see above, the left array has only one element, so it returns immediately.

Next, we call quickSort() on the right array and step 1 and 2 will repeat during this process.

4. Again, we recursively call on right array

5. Finally, we combine the returned value.
You can understand how the returned values are combined with the help of the visual image below.

Quick Sort Algorithm

FUNCTION quickSort(arr):
    IF length of arr <= 1:
        RETURN arr

    SET pivot TO last element of arr
    INITIALIZE left as empty list
    INITIALIZE right as empty list

    FOR each element in arr EXCEPT the last one:
        IF element < pivot:
            ADD element to left
        ELSE:
            ADD element to right

    RETURN quickSort(left) + [pivot] + quickSort(right)

Quick Sort Code

function quickSort(arr) {
  if (arr.length <= 1) return arr;

  let pivot = arr[arr.length - 1];
  let left = [];
  let right = [];

  for (let i = 0; i < arr.length - 1; i++) {
    if (arr[i] < pivot) left[left.length] = arr[i];
    else right[right.length] = arr[i];
  }

  return [...quickSort(left), pivot, ...quickSort(right)];
}

console.log(quickSort([5, -11, 9, 2, 1]));

Quick Sort Complexity

Time Complexity
Best	O(n*log n)
Worst	O(n²)
Average	O(n*log n)
Space Complexity	O(log n)
Stability	No

1. Time Complexities

Worst Case Complexity: O(n²) If the pivot is the smallest or largest number, it goes to the end of the sorted array.

One side becomes empty, and the other side has almost all the elements. So, Quicksort keeps working on the bigger side again and again.

It works much better when the pivot is somewhere in the middle, not at the ends.

Best Case Complexity: O(n log n)
It occurs when the pivot element is always the middle element or near to the middle element.
Average Case Complexity: O(n log n)
It occurs when the above conditions do not occur.

2. Space Complexity

Space Complexity: O(n) The space complexity for quicksort is O(log n).

Applications of Quicksort

1. General Purpose Sorting

Used in libraries and frameworks for sorting numbers, strings, and other data types.
Example: JavaScript's Array.sort() uses a variation of Quicksort under the hood in some engines.

2. Large Datasets