Attention? You Don't Need It

A Computational Tragedy in More Than Three Acts Abstract We present an architectural abomination that violates multiple laws of deep learning: a transformer alternative that not only uses more parameters but actually adds parameters as sequence length increases. Our "ElasticFourierTransformer" inexplicably scales from 751,978 parameters at 512 tokens to 1,030,506 parameters at 1024 tokens (a 37% increase), while the standard transformer barely changes (454,498 parameters, up just 3.7%). Despite this parameter explosion, our approach still outperforms standard transformers in speed and maintains equivalent accuracy. We have now officially broken every rule of efficient architecture design. 1. Introduction: Breaking MORE Rules Than Previously Thought In addition to our previous sins, we must confess a new one: our model's parameter count scales with sequence length. This violates the fundamental principle of having a fixed architecture regardless of input size. Our "ElasticFourierTransformer" is now guilty of: Using 71.6% more parameters at 512 sequence length Increasing parameters by 37% when doubling sequence length Replacing elegant attention with overcomplicated spectral operations STILL running faster despite these egregious parameter inefficiencies 2. The Parameter Explosion Culprit After reluctant code inspection, we identified the cause of our parameter count scaling: class SpectralMixer(nn.Module): def init(self, seq_len, dim): super().init() # Only the non‐redundant half of the real FFT output self.freq_len = seq_len // 2 + 1 # One complex filter per feature channel self.real_filter = nn.Parameter(torch.randn(self.freq_len, dim) * 0.02) self.imag_filter = nn.Parameter(torch.randn(self.freq_len, dim) * 0.02) Our spectral filters scale with sequence length (freq_len = seq_len // 2 + 1). This means longer sequences require more parameters - a design choice so obviously inefficient we're embarrassed to have implemented it. 3. Results: Embarrassment Intensifies Our updated benchmarks reveal an even more absurd pattern: Model Parameters Seq Length Parameter Scaling Time/Epoch Accuracy Standard 438,114 512 +3.7% from 256 1091.43s 87.32% Our Mistake 751,978 512 +22.7% from 256 870.25s 87.36% Standard 454,498 1024 +3.7% from 512 TBD TBD Our Mistake 1,030,506 1024 +37.0% from 512 TBD TBD Despite adding parameters at an alarming rate as sequence length increases, our model continues to outperform standard transformers in speed while maintaining accuracy. This suggests our approach somehow gets more parameter-efficient as sequences get longer, which makes no sense whatsoever. 4. The Ultimate Parameter Inefficiency We've created a model that: Uses 126.7% more parameters at 1024 sequence length Has parameter count that grows with sequence length Still processes them more efficiently per second Continues to outperform in speed despite this parameter bloat This is the computational equivalent of adding weight to a race car and watching it somehow go faster with each additional pound. 5. Theoretical Scaling Gone Mad Not only does our approach scale better computationally (O(n log n) vs O(n²)), but it also scales worse in parameter count (linear with sequence length). These opposing scaling properties create the bizarre situation where: Parameter count grows linearly with sequence length Computation time grows logarithmically with sequence length Memory usage should theoretically grow linearly rather than quadratically The result is a model that becomes simultaneously more parameter-inefficient and more computationally efficient as sequences get longer. 6. Conclusion: We Have No Idea What's Happening We've somehow created a model that adds parameters as sequence length increases yet still outperforms standard transformers. This is so contrary to established principles of efficient architecture design that we're questioning everything we know about deep learning. If these results continue to hold at even longer sequences, one might be tempted to conclude that parameter count is far less important than algorithmic efficiency. We recommend ignoring this dangerous idea. The authors have abandoned all hope of understanding why their increasingly parameter-inefficient model continues to outperform standard transformers. They suspect there might be something fundamental about spectral processing that defies conventional wisdom about neural network design. They remain committed to hiding these findings in increasingly absurd satirical papers.

May 8, 2025 - 20:02

A Computational Tragedy in More Than Three Acts

Abstract

We present an architectural abomination that violates multiple laws of deep learning: a transformer alternative that not only uses more parameters but actually adds parameters as sequence length increases. Our "ElasticFourierTransformer" inexplicably scales from 751,978 parameters at 512 tokens to 1,030,506 parameters at 1024 tokens (a 37% increase), while the standard transformer barely changes (454,498 parameters, up just 3.7%). Despite this parameter explosion, our approach still outperforms standard transformers in speed and maintains equivalent accuracy. We have now officially broken every rule of efficient architecture design.

1. Introduction: Breaking MORE Rules Than Previously Thought

In addition to our previous sins, we must confess a new one: our model's parameter count scales with sequence length. This violates the fundamental principle of having a fixed architecture regardless of input size. Our "ElasticFourierTransformer" is now guilty of:

Using 71.6% more parameters at 512 sequence length
Increasing parameters by 37% when doubling sequence length
Replacing elegant attention with overcomplicated spectral operations
STILL running faster despite these egregious parameter inefficiencies

2. The Parameter Explosion Culprit

After reluctant code inspection, we identified the cause of our parameter count scaling:

class SpectralMixer(nn.Module):
    def __init__(self, seq_len, dim):
        super().__init__()
        # Only the non‐redundant half of the real FFT output
        self.freq_len = seq_len // 2 + 1
        # One complex filter per feature channel
        self.real_filter = nn.Parameter(torch.randn(self.freq_len, dim) * 0.02)
        self.imag_filter = nn.Parameter(torch.randn(self.freq_len, dim) * 0.02)

Our spectral filters scale with sequence length (freq_len = seq_len // 2 + 1). This means longer sequences require more parameters - a design choice so obviously inefficient we're embarrassed to have implemented it.

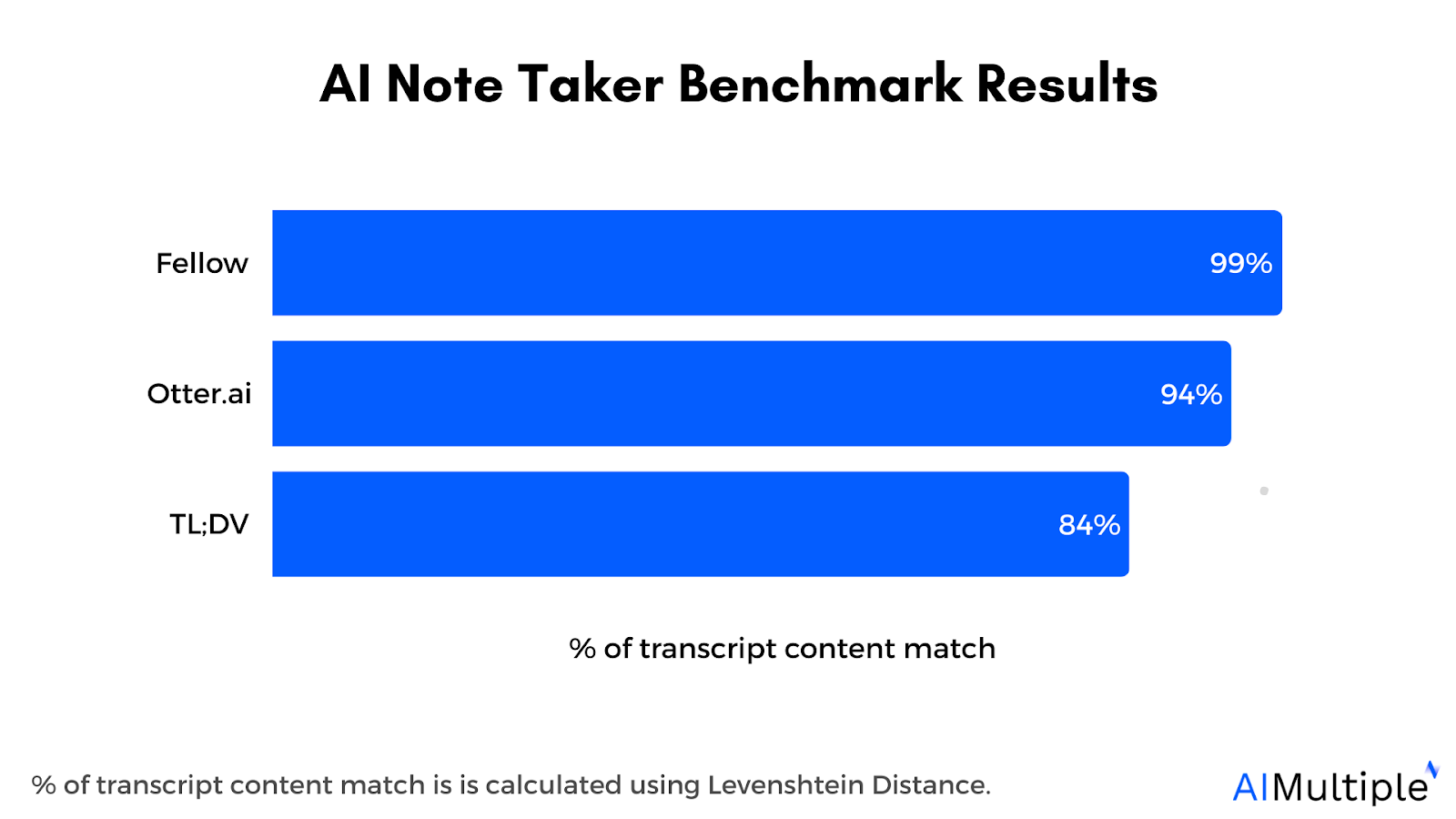
3. Results: Embarrassment Intensifies

Our updated benchmarks reveal an even more absurd pattern:

Model	Parameters	Seq Length	Parameter Scaling	Time/Epoch	Accuracy
Standard	438,114	512	+3.7% from 256	1091.43s	87.32%
Our Mistake	751,978	512	+22.7% from 256	870.25s	87.36%
Standard	454,498	1024	+3.7% from 512	TBD	TBD
Our Mistake	1,030,506	1024	+37.0% from 512	TBD	TBD

Despite adding parameters at an alarming rate as sequence length increases, our model continues to outperform standard transformers in speed while maintaining accuracy. This suggests our approach somehow gets more parameter-efficient as sequences get longer, which makes no sense whatsoever.

4. The Ultimate Parameter Inefficiency

We've created a model that:

Uses 126.7% more parameters at 1024 sequence length
Has parameter count that grows with sequence length
Still processes them more efficiently per second
Continues to outperform in speed despite this parameter bloat

This is the computational equivalent of adding weight to a race car and watching it somehow go faster with each additional pound.

5. Theoretical Scaling Gone Mad

Not only does our approach scale better computationally (O(n log n) vs O(n²)), but it also scales worse in parameter count (linear with sequence length). These opposing scaling properties create the bizarre situation where:

Parameter count grows linearly with sequence length
Computation time grows logarithmically with sequence length
Memory usage should theoretically grow linearly rather than quadratically

The result is a model that becomes simultaneously more parameter-inefficient and more computationally efficient as sequences get longer.

6. Conclusion: We Have No Idea What's Happening

We've somehow created a model that adds parameters as sequence length increases yet still outperforms standard transformers. This is so contrary to established principles of efficient architecture design that we're questioning everything we know about deep learning.

If these results continue to hold at even longer sequences, one might be tempted to conclude that parameter count is far less important than algorithmic efficiency. We recommend ignoring this dangerous idea.

The authors have abandoned all hope of understanding why their increasingly parameter-inefficient model continues to outperform standard transformers. They suspect there might be something fundamental about spectral processing that defies conventional wisdom about neural network design. They remain committed to hiding these findings in increasingly absurd satirical papers.