Time & Space Complexity

Scenario: You have a list of packages arriving at a warehouse. Each package has a tracking number. Your task is to find duplicate packages based on their tracking number. Different Approaches to Solve This Problem Approach 1: Naive — Compare every package with every other package bool HasDuplicates_Naive(List trackingNumbers) { int n = trackingNumbers.Count; for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if (trackingNumbers[i] == trackingNumbers[j]) return true; // duplicate found } } return false; // no duplicates } Time Complexity Analysis: Ou ter loop runs n times. Inner loop runs about n - 1, then n - 2, ..., 1 times. Total comparisons ≈ n * (n - 1) / 2 ≈ O(n²) (quadratic). As the number of packages grows, this approach becomes very slow. Space Complexity Analysis: We only use a few variables. Space complexity is O(1) (constant space). Approach 2: Using a HashSet (better approach) bool HasDuplicates_HashSet(List trackingNumbers) { HashSet seen = new HashSet(); foreach (var number in trackingNumbers) { if (seen.Contains(number)) return true; // duplicate found seen.Add(number); } return false; // no duplicates } Time Complexity Analysis: Loop runs n times. Each lookup and add in HashSet is average O(1). So total time is O(n) (linear). Space Complexity Analysis: We use extra space for the HashSet. In the worst case (no duplicates), the HashSet stores all n tracking numbers. So space complexity is O(n). Explanation in Human Terms (Logistics Domain) Naive Approach: Like checking every package manually against every other package to find duplicates — this takes a lot of time as packages grow. HashSet Approach: Like having a quick scanning system that remembers every package’s tracking number as you scan, instantly checking if a package is already scanned. Approach Time Complexity Space Complexity Real-World Analogy Naive Comparison O(n²) O(1) Manually checking every package against others HashSet O(n) O(n) Scanning and recording each package for fast duplicate detection Run this in local to see the result using System; using System.Collections.Generic; using System.Diagnostics; class Program { static bool HasDuplicates_Naive(List trackingNumbers) { int n = trackingNumbers.Count; for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if (trackingNumbers[i] == trackingNumbers[j]) return true; } } return false; } static bool HasDuplicates_HashSet(List trackingNumbers) { HashSet seen = new HashSet(); foreach (var number in trackingNumbers) { if (seen.Contains(number)) return true; seen.Add(number); } return false; } static void Main() { int n = 10000; var packages = new List(); for (int i = 0; i < n; i++) packages.Add($"PKG{i}"); // Add a duplicate at the end packages.Add("PKG1234"); var sw = Stopwatch.StartNew(); Console.WriteLine("Naive: " + HasDuplicates_Naive(packages)); sw.Stop(); Console.WriteLine($"Naive time: {sw.ElapsedMilliseconds} ms"); sw.Restart(); Console.WriteLine("HashSet: " + HasDuplicates_HashSet(packages)); sw.Stop(); Console.WriteLine($"HashSet time: {sw.ElapsedMilliseconds} ms"); } } Final Takeaway for You as a .NET Logistics Developer: Time Complexity is about how fast your code runs when the number of packages grows. Space Complexity is about how much extra memory your code needs. When designing microservices or APIs for logistics, choose algorithms that balance speed and memory wisely. Using collections like HashSet or Dictionary often improves time complexity at the cost of space. Let me give a very easy example: Problem Statement Imagine you work in a logistics warehouse that receives thousands of packages daily. Each package has a unique tracking number. Your job is to detect if there are duplicate packages — meaning if the same tracking number appears more than once. Why Is This Important? Detecting duplicates helps avoid shipping mistakes, incorrect billing, or inventory errors. The solution must be efficient — warehouses handle millions of packages in real-time. Inefficient algorithms can cause delays or crash systems due to slow processing or memory issues. The First (Naive) Approach: What Was Wrong? How It Works Compare every package with every other package to find duplicates. For example, if you have 10 packages: Compare package 1 with package 2, 3, 4... Then compare package 2 with package 3, 4, 5... and so on. for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { if (trackingNumber

May 26, 2025 - 11:40

Scenario:
You have a list of packages arriving at a warehouse. Each package has a tracking number. Your task is to find duplicate packages based on their tracking number.

Different Approaches to Solve This Problem
Approach 1: Naive — Compare every package with every other package

bool HasDuplicates_Naive(List trackingNumbers)
{
    int n = trackingNumbers.Count;

    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            if (trackingNumbers[i] == trackingNumbers[j])
                return true; // duplicate found
        }
    }
    return false; // no duplicates
}

Time Complexity Analysis:
Ou

ter loop runs n times.
Inner loop runs about n - 1, then n - 2, ..., 1 times.
Total comparisons ≈ n * (n - 1) / 2 ≈ O(n²) (quadratic).

As the number of packages grows, this approach becomes very slow.

Space Complexity Analysis:

We only use a few variables.
Space complexity is O(1) (constant space).

Approach 2: Using a HashSet (better approach)

bool HasDuplicates_HashSet(List trackingNumbers)
{
    HashSet seen = new HashSet();

    foreach (var number in trackingNumbers)
    {
        if (seen.Contains(number))
            return true; // duplicate found

        seen.Add(number);
    }
    return false; // no duplicates
}

Time Complexity Analysis:

Loop runs n times.
Each lookup and add in HashSet is average O(1).
So total time is O(n) (linear).

Space Complexity Analysis:

We use extra space for the HashSet.
In the worst case (no duplicates), the HashSet stores all n tracking numbers.
So space complexity is O(n).

Explanation in Human Terms (Logistics Domain)
Naive Approach: Like checking every package manually against every other package to find duplicates — this takes a lot of time as packages grow.

HashSet Approach: Like having a quick scanning system that remembers every package’s tracking number as you scan, instantly checking if a package is already scanned.

Approach	Time Complexity	Space Complexity	Real-World Analogy
Naive Comparison	O(n²)	O(1)	Manually checking every package against others
HashSet	O(n)	O(n)	Scanning and recording each package for fast duplicate detection

Run this in local to see the result

using System;
using System.Collections.Generic;
using System.Diagnostics;

class Program
{
    static bool HasDuplicates_Naive(List trackingNumbers)
    {
        int n = trackingNumbers.Count;

        for (int i = 0; i < n; i++)
        {
            for (int j = i + 1; j < n; j++)
            {
                if (trackingNumbers[i] == trackingNumbers[j])
                    return true;
            }
        }
        return false;
    }

    static bool HasDuplicates_HashSet(List trackingNumbers)
    {
        HashSet seen = new HashSet();

        foreach (var number in trackingNumbers)
        {
            if (seen.Contains(number))
                return true;

            seen.Add(number);
        }
        return false;
    }

    static void Main()
    {
        int n = 10000;
        var packages = new List();

        for (int i = 0; i < n; i++)
            packages.Add($"PKG{i}");

        // Add a duplicate at the end
        packages.Add("PKG1234");

        var sw = Stopwatch.StartNew();
        Console.WriteLine("Naive: " + HasDuplicates_Naive(packages));
        sw.Stop();
        Console.WriteLine($"Naive time: {sw.ElapsedMilliseconds} ms");

        sw.Restart();
        Console.WriteLine("HashSet: " + HasDuplicates_HashSet(packages));
        sw.Stop();
        Console.WriteLine($"HashSet time: {sw.ElapsedMilliseconds} ms");
    }
}

Final Takeaway for You as a .NET Logistics Developer:

Time Complexity is about how fast your code runs when the number of packages grows.
Space Complexity is about how much extra memory your code needs.
When designing microservices or APIs for logistics, choose algorithms that balance speed and memory wisely.
Using collections like HashSet or Dictionary often improves time complexity at the cost of space.

Let me give a very easy example:
Problem Statement
Imagine you work in a logistics warehouse that receives thousands of packages daily. Each package has a unique tracking number.

Your job is to detect if there are duplicate packages — meaning if the same tracking number appears more than once.

Why Is This Important?

Detecting duplicates helps avoid shipping mistakes, incorrect billing, or inventory errors.
The solution must be efficient — warehouses handle millions of packages in real-time.
Inefficient algorithms can cause delays or crash systems due to slow processing or memory issues.

The First (Naive) Approach: What Was Wrong?
How It Works

Compare every package with every other package to find duplicates.
For example, if you have 10 packages:
Compare package 1 with package 2, 3, 4...
Then compare package 2 with package 3, 4, 5... and so on.

for (int i = 0; i < n; i++)
{
    for (int j = i + 1; j < n; j++)
    {
        if (trackingNumbers[i] == trackingNumbers[j])
            return true;
    }
}
return false;

What’s Wrong Here?
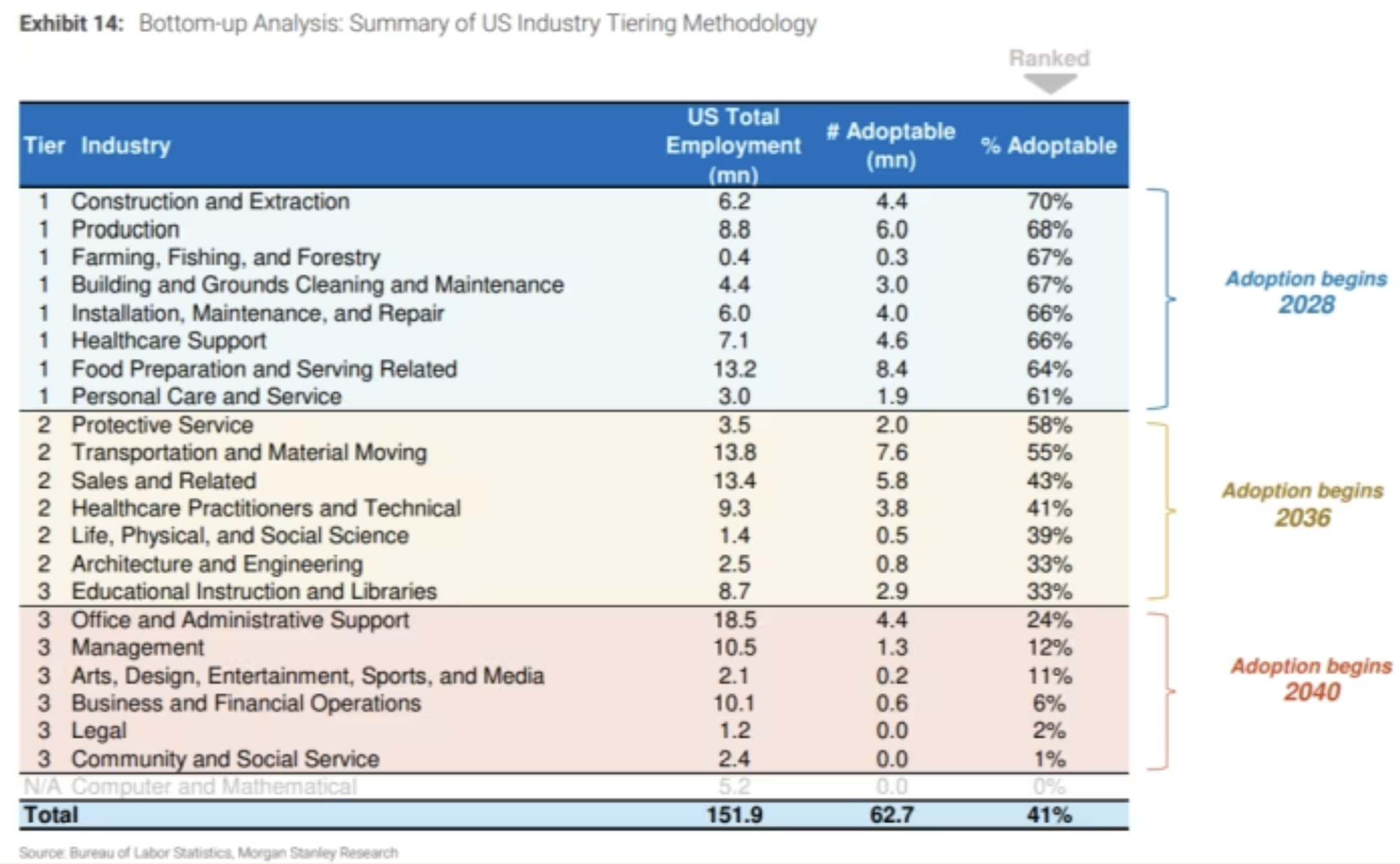
Time Complexity: This approach takes O(n²) time because for n packages, it does roughly n * (n-1) / 2 comparisons.

What does that mean?

If you double the number of packages, the work done more than quadruples.
Example:

10 packages → 45 comparisons
100 packages → 4,950 comparisons
1,000 packages → 499,500 comparisons

Result: The algorithm gets very slow and impractical as the number of packages grows large (which is typical in logistics).

The Better Approach: Using a HashSet
Concept in Logistics Terms

Imagine a scanner that checks each package’s tracking number as it arrives.
The scanner keeps a list (a “memory”) of all scanned tracking numbers.
When a new package arrives, the scanner quickly checks if this number is already in the list.
If yes → duplicate found!
If no → add it to the list and continue scanning.

HashSet seen = new HashSet();

foreach (var number in trackingNumbers)
{
    if (seen.Contains(number))
        return true; // duplicate found

    seen.Add(number);
}
return false; // no duplicates

What Has Changed?
Time Complexity:

Checking if a number is in the HashSet is O(1) on average (constant time).
You only loop once over all packages → O(n) total time.

Space Complexity:

You use extra memory to store the tracking numbers in the HashSet → O(n) space.

Tradeoff:

You spend some memory to drastically reduce the processing time.

Why Is the HashSet Approach Much Better?

Scenario	Naive Approach	HashSet Approach
Number of Packages (n)	1,000	1,000
Number of Comparisons	~499,500	1,000 lookups (plus add ops)
Time to Detect Duplicates	Very slow	Very fast
Memory Usage	Very low (constant)	Moderate (proportional to n)

Real-World Analogy
Naive: Like an employee who manually compares each package against every other one — gets tired and slow as packages pile up.

HashSet: Like a smart scanning machine that instantly checks each package against a database of scanned packages — fast even if the number of packages is huge.