Optimizing the Top K Elements Problem Using a Max-Heap

The Problem The Top K Elements algorithm helps find the k most frequent elements in a list. A naive solution would involve storing all elements and their frequencies as tuples in an array, sorting the array by frequencies in decreasing order, and then returning the first k elements. While this works fine for small datasets, it becomes inefficient as the dataset grows. We can optimize this approach by using a binary heap, which will allow us to store only the top k elements and significantly improve the time complexity. Naive Solution Steps Create a frequency map (using an object) to store the elements and their frequencies. Convert the frequency map into an array of [element, frequency] pairs. Sort the array in decreasing order based on the frequency of elements. Slice the array to extract the top k elements. Return the elements by mapping over the sliced array and retrieving only the elements (ignoring their frequencies). function naiveTopK(list, k) { // Create an object of element frequencies const freqMap = {}; for (const elem of list) { freqMap[elem] = (freqMap[elem] || 0) + 1; } // Convert frequencies object into an array of tuples const freqArr = Object.entries(freqMap); // Sort the frequenciesArr in descending order const sortedArray = freqArr.sort((a, b) => b[1] - a[1]); // Slice and map over the top k elements to return top k occurring return sortedArray.slice(0, k).map((tuple) => { return tuple[0]; }); } Efficiency Issues of the Naive Solution The time complexity of the naive solution is O(n log n), meaning that as the size of the dataset (n) increases, the execution time increases at an accelerating rate. The primary issue with this approach is that it requires storing and sorting the entire array of elements, which becomes inefficient with larger datasets. A binary heap is a binary tree data structure that satisfies the heap property. In a max-heap, each node's value is greater than or equal to the values of its children, while in a min-heap, each node's value is less than or equal to the values of its children. By using a binary heap to store only the top k most frequent elements, we can significantly improve time complexity. This optimized solution reduces the complexity to O(n log k), where k is the number of elements we need to track, leading to better performance with larger datasets. Create a MaxHeap Class We will implement a MaxHeap class to efficiently store the top k elements of the list. The class will include several methods: size: Returns the current number of elements in the heap push: Adds a new element to the heap pop: Removes the root (largest element) of the heap and returns it removeSmallest: Removes the least occurring element from the heap _heapifyUp: Balances the heap when new elements are added, ensuring the max-heap property is maintained _heapifyDown: Balances the heap when the root is removed, ensuring the max-heap property is maintained // Create a MaxHeap class class MaxHeap { constructor() { this.heap = []; } size() { return this.heap.length; } push(item) { this.heap.push(item); // Ensure the heap is balanced this._heapifyUp(); } removeSmallest() { this.heap.pop(); } pop() { if (this.size() === 0) return null; // Store the old root to be returned const root = this.heap[0]; // Reassign the root to the last element to maintain the heap structure this.heap[0] = this.heap[this.size() - 1]; // Remove the last element from the heap since it is now a duplicate this.heap.pop(); // Ensure the heap is balanced this._heapifyDown(); return root; } // Ensure the max heap maintains balance by making sure element is added in the correct place _heapifyUp() { // Start with the last element (this is where new elements are inserted) let index = this.size() - 1; // While the index is greater than 0 while (index > 0) { // Find the parent index const parentIndex = Math.floor((index - 1) / 2); // If parent is greater than child the heap property is satisfied and we can stop if (this.heap[parentIndex][1] > this.heap[index][1]) { return; } else { // Flip the parent and child elements [this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]]; // Set the index to the parent index index = parentIndex; } } } // Keep balance of the heap when the root is removed _heapifyDown() { let parentIndex = 0; const length = this.size(); // While there is at least one child while (2 * parentIndex + 1 this.heap[largestElemIndex][1]) { // Reassign the current largestElemIndex largestElemIndex = leftIndex; } // Check if right child exists and is larger than the current largest if (rightIndex this.heap[largestElemIndex][1]) { // Reassign the cu

Apr 9, 2025 - 19:16

Optimizing the Top K Elements Problem Using a Max-Heap

The Problem

The Top K Elements algorithm helps find the k most frequent elements in a list. A naive solution would involve storing all elements and their frequencies as tuples in an array, sorting the array by frequencies in decreasing order, and then returning the first k elements. While this works fine for small datasets, it becomes inefficient as the dataset grows. We can optimize this approach by using a binary heap, which will allow us to store only the top k elements and significantly improve the time complexity.

Naive Solution Steps

Create a frequency map (using an object) to store the elements and their frequencies.
Convert the frequency map into an array of [element, frequency] pairs.
Sort the array in decreasing order based on the frequency of elements.
Slice the array to extract the top k elements.
Return the elements by mapping over the sliced array and retrieving only the elements (ignoring their frequencies).

function naiveTopK(list, k) {
  // Create an object of element frequencies
  const freqMap = {};
  for (const elem of list) {
    freqMap[elem] = (freqMap[elem] || 0) + 1;
  }
  // Convert frequencies object into an array of tuples
  const freqArr = Object.entries(freqMap);
  // Sort the frequenciesArr in descending order
  const sortedArray = freqArr.sort((a, b) => b[1] - a[1]);
  // Slice and map over the top k elements to return top k occurring
  return sortedArray.slice(0, k).map((tuple) => {
    return tuple[0];
  });
}

Efficiency Issues of the Naive Solution

The time complexity of the naive solution is O(n log n), meaning that as the size of the dataset (n) increases, the execution time increases at an accelerating rate. The primary issue with this approach is that it requires storing and sorting the entire array of elements, which becomes inefficient with larger datasets.

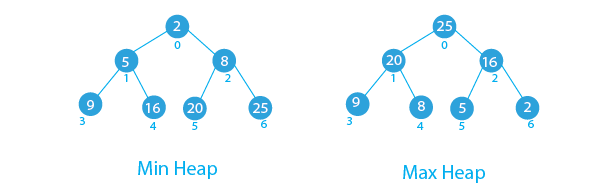
A binary heap is a binary tree data structure that satisfies the heap property. In a max-heap, each node's value is greater than or equal to the values of its children, while in a min-heap, each node's value is less than or equal to the values of its children. By using a binary heap to store only the top k most frequent elements, we can significantly improve time complexity. This optimized solution reduces the complexity to O(n log k), where k is the number of elements we need to track, leading to better performance with larger datasets.

Create a MaxHeap Class

We will implement a MaxHeap class to efficiently store the top k elements of the list. The class will include several methods:

size: Returns the current number of elements in the heap
push: Adds a new element to the heap
pop: Removes the root (largest element) of the heap and returns it
removeSmallest: Removes the least occurring element from the heap
_heapifyUp: Balances the heap when new elements are added, ensuring the max-heap property is maintained
_heapifyDown: Balances the heap when the root is removed, ensuring the max-heap property is maintained

// Create a MaxHeap class
class MaxHeap {
  constructor() {
    this.heap = [];
  }
  size() {
    return this.heap.length;
  }
  push(item) {
    this.heap.push(item);
    // Ensure the heap is balanced
    this._heapifyUp();
  }
  removeSmallest() {
    this.heap.pop();
  }
  pop() {
    if (this.size() === 0) return null;
    // Store the old root to be returned
    const root = this.heap[0];
    // Reassign the root to the last element to maintain the heap structure
    this.heap[0] = this.heap[this.size() - 1];
    // Remove the last element from the heap since it is now a duplicate
    this.heap.pop();
    // Ensure the heap is balanced
    this._heapifyDown();
    return root;
  }
  // Ensure the max heap maintains balance by making sure element is added in the correct place
  _heapifyUp() {
    // Start with the last element (this is where new elements are inserted)
    let index = this.size() - 1;
    // While the index is greater than 0
    while (index > 0) {
      // Find the parent index
      const parentIndex = Math.floor((index - 1) / 2);
      // If parent is greater than child the heap property is satisfied and we can stop
      if (this.heap[parentIndex][1] > this.heap[index][1]) {
        return;
      } else {
        // Flip the parent and child elements
        [this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]];
        // Set the index to the parent index
        index = parentIndex;
      }
    }
  }
  // Keep balance of the heap when the root is removed
  _heapifyDown() {
    let parentIndex = 0;
    const length = this.size();
    // While there is at least one child
    while (2 * parentIndex + 1 < this.size()) {
      // We assume the largest element index is at the front
      let largestElemIndex = parentIndex;
      const leftIndex = 2 * parentIndex + 1;
      const rightIndex = 2 * parentIndex + 2;
      // Check if left child frequency is larger than the current largest
      if (this.heap[leftIndex][1] > this.heap[largestElemIndex][1]) {
        // Reassign the current largestElemIndex
        largestElemIndex = leftIndex;
      }
      // Check if right child exists and is larger than the current largest
      if (rightIndex < length && this.heap[rightIndex][1] > this.heap[largestElemIndex][1]) {
        // Reassign the current largestElemIndex
        largestElemIndex = rightIndex;
      }
      // If largest is not the current node (one of the children was larger than the parent), swap and continue
      if (largestElemIndex !== parentIndex) {
        // Swap the current largest with the parent
        [this.heap[parentIndex], this.heap[largestElemIndex]] = [this.heap[largestElemIndex], this.heap[parentIndex]];
        // Reassign the parentIndex to the largestElemIndex
        parentIndex = largestElemIndex;
      } else {
        return; // No swap needed, heap is in valid state
      }
    }
  }
}

Optimized Solution

Once our MaxHeap class is configured, we can create an instance of the class in order to store our top k elements. This prevents us from having to eventually sort every element in the list.

function optimizedTopK(list, k) {
  // Create an object of element frequencies
  const freqMap = {};
  for (let elem of list) {
    // Add the elements to freqMap or increase the frequency count
    freqMap[elem] = (freqMap[elem] || 0) + 1;
  }
  // Create an instance of MaxHeap to store the most frequent elements
  const heap = new MaxHeap();
  // Add the tuples to the heap
  for (const [num, freq] of Object.entries(freqMap)) {
    heap.push([num, freq]);
    // Check if the heap's size exceeds the desired number of top elements (k)
    if (heap.size() > k) {
      heap.removeSmallest();
    }
  }
  // Return the most frequent elements from the heap
  return heap.heap.map(elem => elem[0])
}
console.log(optimizedTopK([1, 1, 1, 2, 2, 3], 2)); // Output: ['1', '2']

_heapifyUp and _heapifyDown

These methods ensure that the max-heap property is maintained, meaning each parent element is greater than or equal to its children, whenever an element is added or removed from the heap.

The _heapifyUp method is called whenever a new element is added to the heap. It starts from the newly added element and moves upwards, comparing its frequency with its parent's frequency. If the new element's frequency is greater than its parent's, the two elements are swapped. This process continues until the max-heap property is satisfied, meaning the parent element is greater than or equal to the child.

The _heapifyDown method is used when the root is removed from the heap. In this solution, we never remove the root, so _heapifyDown isn’t called. However, if we were using pop()—for example, in a variation of this algorithm or a min-heap version—we’d rely on _heapifyDown to maintain heap order. It checks if either of the two child nodes has a greater frequency than the parent. If one of the child's frequencies is greater than the parent's, the elements are swapped, and the process repeats until the heap property is restored.

Conclusion

The naive solution to the Top K Elements problem works fine for smaller datasets, but as the dataset grows, sorting the entire list becomes inefficient. By implementing a max-heap, we can avoid sorting the entire list and instead focus on maintaining just the top k elements. This optimization reduces our time complexity from O(n log n) to O(n log k), significantly improving performance for larger datasets.