Binary Search

Binary Search is a searching algorithm to find an element in a sorted array by repeatedly dividing the search range in half. It compares the target with the middle element and narrows the search to either the left or right half accordingly. Note : Binary search can be implemented only on a sorted list of items. If the elements are not sorted already, we need to sort them first. Working of Binary Search Binary Search Algorithm can be implemented in two ways which are discussed below. 1. Iterative Method 2. Recursive Method The recursive method follows the divide and conquer approach. 1. Start with a sorted array. Let x = 18 be the element to be searched. 2. Set two pointers low and high at the lowest and the highest positions respectively. 3. Find the middle position mid of the array ie. mid = (low + high)/2 and arr[mid] = 12. 4. If x == arr[mid], then return mid. Else, compare the element to be searched with arr[mid]. 5. If x > arr[mid], compare x with the middle element of the elements on the right side of arr[mid]. This is done by setting low to low = mid + 1. 6. Else, compare x with the middle element of the elements on the left side of arr[mid]. This is done by setting high to high = mid - 1. 7. Repeat steps 3 to 6 until low meets high. 8. x = 18 is found. Binary Search Algorithm in iterative method function binarySearch(array, target): set low to 0 set high to length of array - 1 while low is less than or equal to high: set mid to (low + high) divided by 2 (rounded down) if array[mid] equals target: return mid (position found) else if array[mid] is greater than target: set high to mid - 1 (search left half) else: set low to mid + 1 (search right half) return -1 (target not found) Binary Search Code in iterative method function binarySearch(arr, k) { let low = 0; let high = arr.length - 1; let mid; while (high >= low) { mid = Math.floor((high + low) / 2); if (arr[mid] === k) return mid; else if (arr[mid] > k) high = mid - 1; else low = mid + 1; } return -1; } console.log(binarySearch([3, 6, 7, 18, 34], 18)); Binary Search Algorithm in recursive method function binarySearch(array, target, low = 0, high = array.length - 1): if low > high: return -1 mid = (low + high) if array[mid] == target: return mid else if array[mid] > target: return binarySearch(array, target, low, mid - 1) else: return binarySearch(array, target, mid + 1, high) Binary Search code in recursive method function binarySearch(arr, k, low = 0, high = arr.length - 1) { if (low > high) return -1; const mid = Math.floor((low + high) / 2); if (arr[mid] === k) return mid; else if (arr[mid] > k) return binarySearch(arr, k, low, mid - 1); else return binarySearch(arr, k, mid + 1, high); } console.log(binarySearch([3, 8, 12, 18, 34], 18)); Time Complexities Best case complexity: O(1) Average case complexity: O(log n) Worst case complexity: O(log n) Space Complexity The space complexity of the binary search is O(1). Real-World Applications of Binary Search

Apr 11, 2025 - 13:09

Binary Search is a searching algorithm to find an element in a sorted array by repeatedly dividing the search range in half.
It compares the target with the middle element and narrows the search to either the left or right half accordingly.

Note :

Binary search can be implemented only on a sorted list of items. If the elements are not sorted already, we need to sort them first.

Working of Binary Search

Binary Search Algorithm can be implemented in two ways which are discussed below.

1. Iterative Method
2. Recursive Method

The recursive method follows the divide and conquer approach.

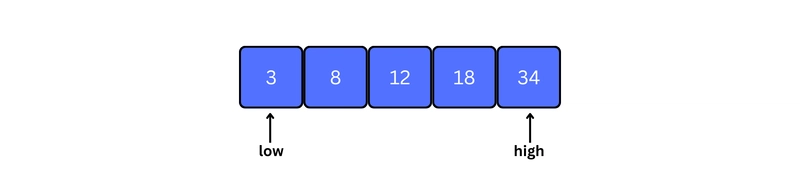
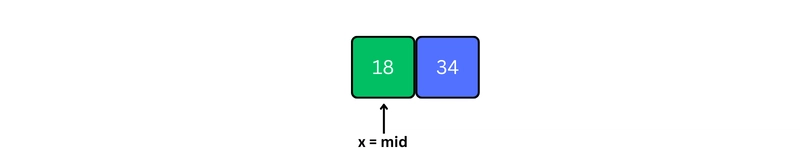
1. Start with a sorted array.

Let x = 18 be the element to be searched.

2. Set two pointers low and high at the lowest and the highest positions respectively.

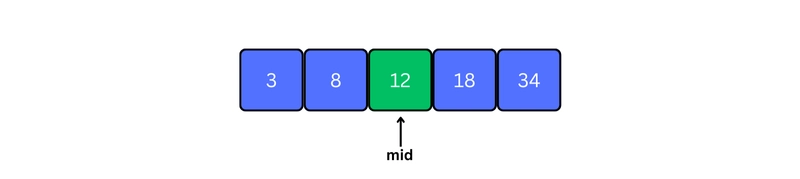
3. Find the middle position mid of the array ie. mid = (low + high)/2 and arr[mid] = 12.

4. If x == arr[mid], then return mid. Else, compare the element to be searched with arr[mid].

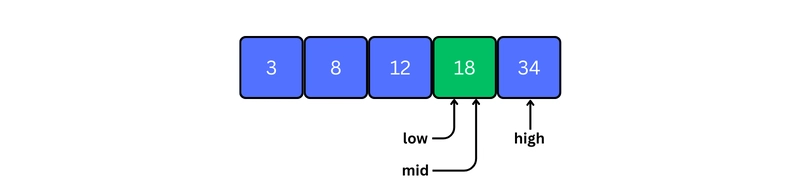
5. If x > arr[mid], compare x with the middle element of the elements on the right side of arr[mid]. This is done by setting low to low = mid + 1.

6. Else, compare x with the middle element of the elements on the left side of arr[mid]. This is done by setting high to high = mid - 1.

7. Repeat steps 3 to 6 until low meets high.

8. x = 18 is found.

Binary Search Algorithm in iterative method

function binarySearch(array, target):
    set low to 0
    set high to length of array - 1

    while low is less than or equal to high:
        set mid to (low + high) divided by 2 (rounded down)

        if array[mid] equals target:
            return mid (position found)

        else if array[mid] is greater than target:
            set high to mid - 1 (search left half)

        else:
            set low to mid + 1 (search right half)

    return -1 (target not found)

Binary Search Code in iterative method

function binarySearch(arr, k) {
  let low = 0;
  let high = arr.length - 1;
  let mid;

  while (high >= low) {
    mid = Math.floor((high + low) / 2);

    if (arr[mid] === k) return mid;
    else if (arr[mid] > k) high = mid - 1;
    else low = mid + 1;
  }

  return -1;
}

console.log(binarySearch([3, 6, 7, 18, 34], 18));

Binary Search Algorithm in recursive method

function binarySearch(array, target, low = 0, high = array.length - 1):
    if low > high:
        return -1  

    mid = (low + high)

    if array[mid] == target:
        return mid  
    else if array[mid] > target:
        return binarySearch(array, target, low, mid - 1)  
    else:
        return binarySearch(array, target, mid + 1, high)

Binary Search code in recursive method

function binarySearch(arr, k, low = 0, high = arr.length - 1) {
  if (low > high) return -1;

  const mid = Math.floor((low + high) / 2);

  if (arr[mid] === k) return mid;
  else if (arr[mid] > k) return binarySearch(arr, k, low, mid - 1);
  else return binarySearch(arr, k, mid + 1, high);
}

console.log(binarySearch([3, 8, 12, 18, 34], 18));

Time Complexities

Best case complexity: O(1)
Average case complexity: O(log n)
Worst case complexity: O(log n)

Space Complexity
The space complexity of the binary search is O(1).