Why Functional Programming vs. Imperative/OOP Matters

Functional programming (FP) emphasizes what you want—transforming data via pure functions—whereas imperative or object‐oriented (OOP) code focuses on how to modify state step by step. Below is a tiny comparison showing how the same task looks in each style: 1. Mapping over a list Imperative (JavaScript): const nums = [1, 2, 3, 4]; let doubled = []; for (let i = 0; i x * 2); console.log(doubled); // [2, 4, 6, 8] Notice how the FP version avoids manual loops and in‐place mutations. You simply describe “map each element to x * 2.” 2. Filtering objects Imperative (Python): people = [ {"name": "Alice", "age": 17}, {"name": "Bob", "age": 22}, {"name": "Cara", "age": 15}, {"name": "Dan", "age": 30} ] adults = [] for person in people: if person["age"] >= 18: adults.append(person) print(adults) # [{'name': 'Bob', 'age': 22}, {'name': 'Dan', 'age': 30}] Functional (Python): people = [ {"name": "Alice", "age": 17}, {"name": "Bob", "age": 22}, {"name": "Cara", "age": 15}, {"name": "Dan", "age": 30} ] # “filter” declares what we want: only those age ≥ 18 adults = list(filter(lambda p: p["age"] >= 18, people)) print(adults) # [{'name': 'Bob', 'age': 22}, {'name': 'Dan', 'age': 30}] Again, FP avoids manually managing a loop and a separate “append” step: you focus only on the filtering logic. 3. Computing a factorial Imperative/OOP (Java): public class Factorial { public static int factorial(int n) { int result = 1; for (int i = 2; i Integer factorial 0 = 1 factorial n = n * factorial (n - 1) main = print (factorial 5) -- 120 In Haskell’s FP style, there is no mutable result variable. You define the base case (0 → 1) and a single recursive rule (n → n * factorial (n-1)), clearly expressing what the factorial is. Why This Comparison Matters Readability & Maintainability: FP code often ends up shorter and more declarative. You see immediately “map these numbers” or “filter these objects” without scanning loop constructs. Fewer Side Effects: By relying on pure functions and immutable data, FP reduces bugs caused by inadvertent state changes—a huge win in concurrent or serverless environments. Testability: Pure functions with no hidden dependencies are easy to test in isolation. Imperative/OOP code often requires setting up state or mocking objects before testing. ❓ Want to dive deeper? In my full blog post I cover: Core FP concepts (pure functions, immutability, higher‐order functions, lazy evaluation) A survey of popular FP languages (Haskell, Scala, F#, JavaScript, Python) and real‐world use cases Practical tips for bringing FP thinking into your existing JavaScript or Python projects

Jun 3, 2025 - 09:50

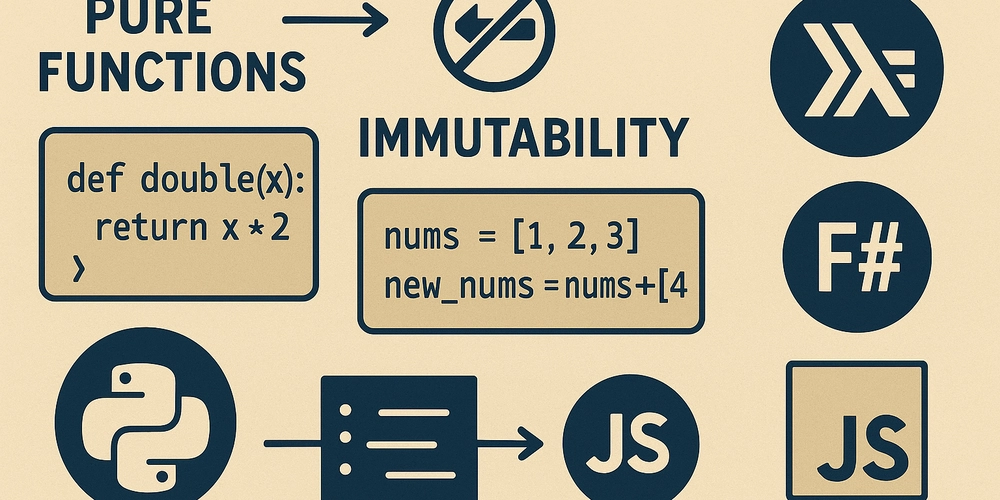
Why Functional Programming vs. Imperative/OOP Matters

Functional programming (FP) emphasizes what you want—transforming data via pure functions—whereas imperative or object‐oriented (OOP) code focuses on how to modify state step by step. Below is a tiny comparison showing how the same task looks in each style:

1. Mapping over a list

Imperative (JavaScript):

const nums = [1, 2, 3, 4];
let doubled = [];
for (let i = 0; i < nums.length; i++) {
  doubled.push(nums[i] * 2);
}
console.log(doubled); // [2, 4, 6, 8]

Functional (JavaScript):

const nums = [1, 2, 3, 4];
// “map” declares *what* we want: double each element
const doubled = nums.map(x => x * 2);
console.log(doubled); // [2, 4, 6, 8]

Notice how the FP version avoids manual loops and in‐place mutations. You simply describe “map each element to x * 2.”

2. Filtering objects

Imperative (Python):

people = [
    {"name": "Alice", "age": 17},
    {"name": "Bob",   "age": 22},
    {"name": "Cara",  "age": 15},
    {"name": "Dan",   "age": 30}
]
adults = []
for person in people:
    if person["age"] >= 18:
        adults.append(person)
print(adults)
# [{'name': 'Bob', 'age': 22}, {'name': 'Dan', 'age': 30}]

Functional (Python):

people = [
    {"name": "Alice", "age": 17},
    {"name": "Bob",   "age": 22},
    {"name": "Cara",  "age": 15},
    {"name": "Dan",   "age": 30}
]
# “filter” declares *what* we want: only those age ≥ 18
adults = list(filter(lambda p: p["age"] >= 18, people))
print(adults)
# [{'name': 'Bob', 'age': 22}, {'name': 'Dan', 'age': 30}]

Again, FP avoids manually managing a loop and a separate “append” step: you focus only on the filtering logic.

3. Computing a factorial

Imperative/OOP (Java):

public class Factorial {
    public static int factorial(int n) {
        int result = 1;
        for (int i = 2; i <= n; i++) {
            result *= i;
        }
        return result;
    }
    public static void main(String[] args) {
        System.out.println(factorial(5)); // 120
    }
}

Functional (Haskell):

-- “recursion” and no mutable state
factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n - 1)

main = print (factorial 5)  -- 120

In Haskell’s FP style, there is no mutable result variable. You define the base case (0 → 1) and a single recursive rule (n → n * factorial (n-1)), clearly expressing what the factorial is.

Why This Comparison Matters

Readability & Maintainability: FP code often ends up shorter and more declarative. You see immediately “map these numbers” or “filter these objects” without scanning loop constructs.
Fewer Side Effects: By relying on pure functions and immutable data, FP reduces bugs caused by inadvertent state changes—a huge win in concurrent or serverless environments.
Testability: Pure functions with no hidden dependencies are easy to test in isolation. Imperative/OOP code often requires setting up state or mocking objects before testing.

❓ Want to dive deeper? In my full blog post I cover:

Core FP concepts (pure functions, immutability, higher‐order functions, lazy evaluation)
A survey of popular FP languages (Haskell, Scala, F#, JavaScript, Python) and real‐world use cases
Practical tips for bringing FP thinking into your existing JavaScript or Python projects