Monotone Triangulation. Practical Advice.
It all started innocently enough. Back in 2009, I just wanted to port Earcut to Flash for a mini-game I was working on. And honestly? It worked — for a while. But over time, I realized that simple solutions tend to fall apart the moment you try to push them to their limits. That’s when I dove into the theory - digging through research papers, YouTube tutorials, and whatever else I could find. One of the most helpful resources was a book by A.V. Skvortsov. Eventually, I landed on the classic approach: decomposing a polygon into monotone pieces. It seemed obvious. And oh - I hit every possible wall while trying to make it work. The first big insight? Replace float with int. That alone got me almost there. But the algorithm was still fragile. Really fragile. Self-intersections, collinear edges, holes touching the outer contour, degenerate points — any of these could break it at any moment. It was functional, but I didn’t like it. Years passed. I wrote iOverlay, a Boolean operations library that can clean up self-intersections and prepare input data properly. And with that tool in hand, I went back to my old triangulator — this time, with the intent to rebuild it from the ground up. Everything went smoother. I knew what to expect. And once you can trust your input data, it's like a rainbow lights up in the sky. Eventually, I realized that monotone partitioning is just an abstraction — and I could drop it entirely. I also polished the Delaunay condition until it shined. That’s how my custom sweep-line triangulation was born. It's not only fast and simple — it’s incredibly stable. I’ve run over a billion randomized tests. And the output? Bit-for-bit consistent. Let’s Get to It As I mentioned earlier, input format is critical for this kind of algorithm. So let’s lock down the strict requirements right away: No self-intersections Contours may only touch each other at a single point Outer contours must be counter-clockwise Holes must be clockwise These are non-negotiable. If your input doesn’t follow these rules, fix it first - iOverlay can help with that. Step 1: Pick a Sweep Direction Since this is a sweep-line algorithm, the first thing we need is to decide the sweep direction. I prefer a left-to-right sweep - moving the line along the X-axis. We sort all vertices based on their coordinates: First by x If x is the same, then by y Simple, but crucial. Edge Case: Touching Points One subtle problem arises when multiple contours converge at a single point - say, an outer contour and one or more holes. There can be an infinite number of variations, but they all have something in common: The number of edges at such a point is always even, If you walk around the point, the edges will alternate: incoming / outgoing / incoming / outgoing... Step 2: Vertex Structure Each vertex needs to "know" its immediate neighbors along the contour. So we store both prev and next references. Something like this works well: struct ChainVertex { index: usize, // ID of the logical point this: Point, // Coordinates of the current vertex next: Point, // Next point in the contour prev: Point, // Previous point in the contour } index: the unique ID for the logical point. Identical points across contours (e.g., touching corners) share the same index. this: coordinates of the current vertex. prev / next: neighbor vertices in the same contour (either outer or hole). This structure is essential for analyzing the local geometry around each point - especially when we classify vertices. Step 3: Vertex Classification Now comes a key part: classifying each vertex. Sweep-line algorithms rely heavily on this step to decide how each vertex should be handled. Classification depends on: The internal angle at the vertex The relative vertical position of neighbors The winding direction of the contour Here are the all types: Start - The beginning of a monotone polygon End - The end of a monotone polygon Split - A vertex that splits the monotone polygon Merge - A vertex where two monotone polygons merge back together Join - A neutral vertex — equal to prev or next Step 4: Sweep and On-the-Fly Triangulation Tracking Active Sections We represent a monotone polygon as a section, which can be: just a point (newly started polygon) a chain of edges. Each section has a support edge (drawn in blue), used as a key in a balanced tree. This edge is either: the next contour edge, or helper edge (bridge between polygon parts) Section structure in code: enum Content { Point(IndexPoint), Edges(Vec), } struct Section { sort: VSegment, // Sorting key in the tree content: Content, } We keep all sections in a balanced tree ordered vertically by their support edge. I’ve already explained how to sort vertical segments in the article. I won’t repeat it here. Every time we po

It all started innocently enough.
Back in 2009, I just wanted to port Earcut to Flash for a mini-game I was working on. And honestly? It worked — for a while. But over time, I realized that simple solutions tend to fall apart the moment you try to push them to their limits.
That’s when I dove into the theory - digging through research papers, YouTube tutorials, and whatever else I could find. One of the most helpful resources was a book by A.V. Skvortsov. Eventually, I landed on the classic approach: decomposing a polygon into monotone pieces. It seemed obvious. And oh - I hit every possible wall while trying to make it work.
The first big insight? Replace float with int. That alone got me almost there. But the algorithm was still fragile. Really fragile. Self-intersections, collinear edges, holes touching the outer contour, degenerate points — any of these could break it at any moment. It was functional, but I didn’t like it.
Years passed. I wrote iOverlay, a Boolean operations library that can clean up self-intersections and prepare input data properly. And with that tool in hand, I went back to my old triangulator — this time, with the intent to rebuild it from the ground up.
Everything went smoother. I knew what to expect. And once you can trust your input data, it's like a rainbow lights up in the sky.
Eventually, I realized that monotone partitioning is just an abstraction — and I could drop it entirely. I also polished the Delaunay condition until it shined.
That’s how my custom sweep-line triangulation was born. It's not only fast and simple — it’s incredibly stable. I’ve run over a billion randomized tests. And the output? Bit-for-bit consistent.
Let’s Get to It
As I mentioned earlier, input format is critical for this kind of algorithm. So let’s lock down the strict requirements right away:
- No self-intersections
- Contours may only touch each other at a single point
- Outer contours must be counter-clockwise
- Holes must be clockwise
These are non-negotiable. If your input doesn’t follow these rules, fix it first - iOverlay can help with that.
Step 1: Pick a Sweep Direction
Since this is a sweep-line algorithm, the first thing we need is to decide the sweep direction. I prefer a left-to-right sweep - moving the line along the X-axis.
We sort all vertices based on their coordinates:
- First by
x - If
xis the same, then byy
Simple, but crucial.
Edge Case: Touching Points
One subtle problem arises when multiple contours converge at a single point - say, an outer contour and one or more holes. There can be an infinite number of variations, but they all have something in common:
- The number of edges at such a point is always even,
- If you walk around the point, the edges will alternate: incoming / outgoing / incoming / outgoing...
Step 2: Vertex Structure
Each vertex needs to "know" its immediate neighbors along the contour. So we store both prev and next references.
Something like this works well:
struct ChainVertex {
index: usize, // ID of the logical point
this: Point, // Coordinates of the current vertex
next: Point, // Next point in the contour
prev: Point, // Previous point in the contour
}
-
index: the unique ID for the logical point. Identical points across contours (e.g., touching corners) share the same index. -
this: coordinates of the current vertex. -
prev/next: neighbor vertices in the same contour (either outer or hole).
This structure is essential for analyzing the local geometry around each point - especially when we classify vertices.
Step 3: Vertex Classification
Now comes a key part: classifying each vertex.
Sweep-line algorithms rely heavily on this step to decide how each vertex should be handled.
Classification depends on:
- The internal angle at the vertex
- The relative vertical position of neighbors
- The winding direction of the contour
Here are the all types:
- Start - The beginning of a monotone polygon
- End - The end of a monotone polygon
- Split - A vertex that splits the monotone polygon
- Merge - A vertex where two monotone polygons merge back together
- Join - A neutral vertex — equal to prev or next
Step 4: Sweep and On-the-Fly Triangulation
Tracking Active Sections
We represent a monotone polygon as a section, which can be:
- just a point (newly started polygon)
- a chain of edges.
Each section has a support edge (drawn in blue), used as a key in a balanced tree. This edge is either:
- the next contour edge, or
- helper edge (bridge between polygon parts)
Section structure in code:
enum Content {
Point(IndexPoint),
Edges(Vec),
}
struct Section {
sort: VSegment, // Sorting key in the tree
content: Content,
}
We keep all sections in a balanced tree ordered vertically by their support edge. I’ve already explained how to sort vertical segments in the article. I won’t repeat it here.
Every time we pop a vertex from the sorted list, we must decide:
Which section does it belong to?
To answer, we search the tree for the closest section below the vertex.
Example: Sections A, B, and C are active. P belongs to B.
Triangle Construction
Once we find the section, we try to form new triangles. Sections keep their edge chains in counter-clockwise order. For each edge, we test if a new triangle (with the current point) forms a counter-clockwise triangle:
- if yes, we add the triangle
- then update the edge chain
Example: Section has edges AC and CD. P forms triangle CDP, but not ACP. The new section contains edges AC and CP, with PE as a new support edge.

Edge structure which also retain triangle info:
struct TriangleEdge {
a: IndexPoint,
b: IndexPoint,
kind: EdgeType, // needed to find triangle neighbors
}
We will collect our triangles in a structure like:
struct Triangle {
vertices: [IndexPoint; 3],
neighbors: [usize; 3],
}
Each triangle is stored with its vertices in counter-clockwise order. We also track neighboring triangles — one per edge.
We store neighbors by index, in the slot opposite to the corresponding edge.
Example: Triangle ABC has neighbors [2, None, 1]
- neighbor across edge (A)BC → triangle 2
- neighbor across edge (B)CA → none
- neighbor across edge (C)AB → triangle 0
Phantom edges
Sometimes, while building triangles, an internal edge is added before it has a neighbor.
We call this a phantom edge — it temporarily "hangs" in the air.
On the first visit, such an edge is converted into a normal internal edge by connecting it to the new triangle.
Example. Edge 3–5 was added as a phantom.

Step 5 (optional): Introduction to Delaunay
At this point, we already have a valid triangulation. But if we want to improve triangle quality, we can enforce the Delaunay condition.
The Delaunay condition ensures that no vertex lies inside the circumcircle of any triangle.
The process is straightforward:
- for each edge shared by two adjacent triangles, we check the Delaunay condition.
- if the condition is violated, we remove the shared edge.
- we then re-triangulate the four involved points by connecting the two opposite vertices (edge flip).
- this process is repeated until no violations remain.
I won’t go into the geometric predicate here — I’ve already covered it in a dedicated article with animations.
Example Non-Delaunay triangles must be flipped into Delaunay triangles

Why does it work?
Each flip reduces the largest (often obtuse) angle between the triangle pair.
This makes the process monotonically convergent — it’s guaranteed to terminate.
In floating-point implementations, this is where bugs can appear.
Due to rounding errors, some flips can alternate endlessly. This is a classic issue, often referred to as the "regular hexagon problem".
But with int or fixed-point logic, the situation improves dramatically:
- the Delaunay check becomes strict and exact
- all operations are deterministic
- no infinite loops — ever
That’s the power of integer-based geometry.
I'll Take It
If you’re interested in trying this in action, check out iTriangle — the Rust library where all of this comes together.
Beyond what I’ve covered here, it includes:
- Tessellation
- Convex polygon partitioning
- Centroid construction
- Steiner points
You can experiment with interactive demos:
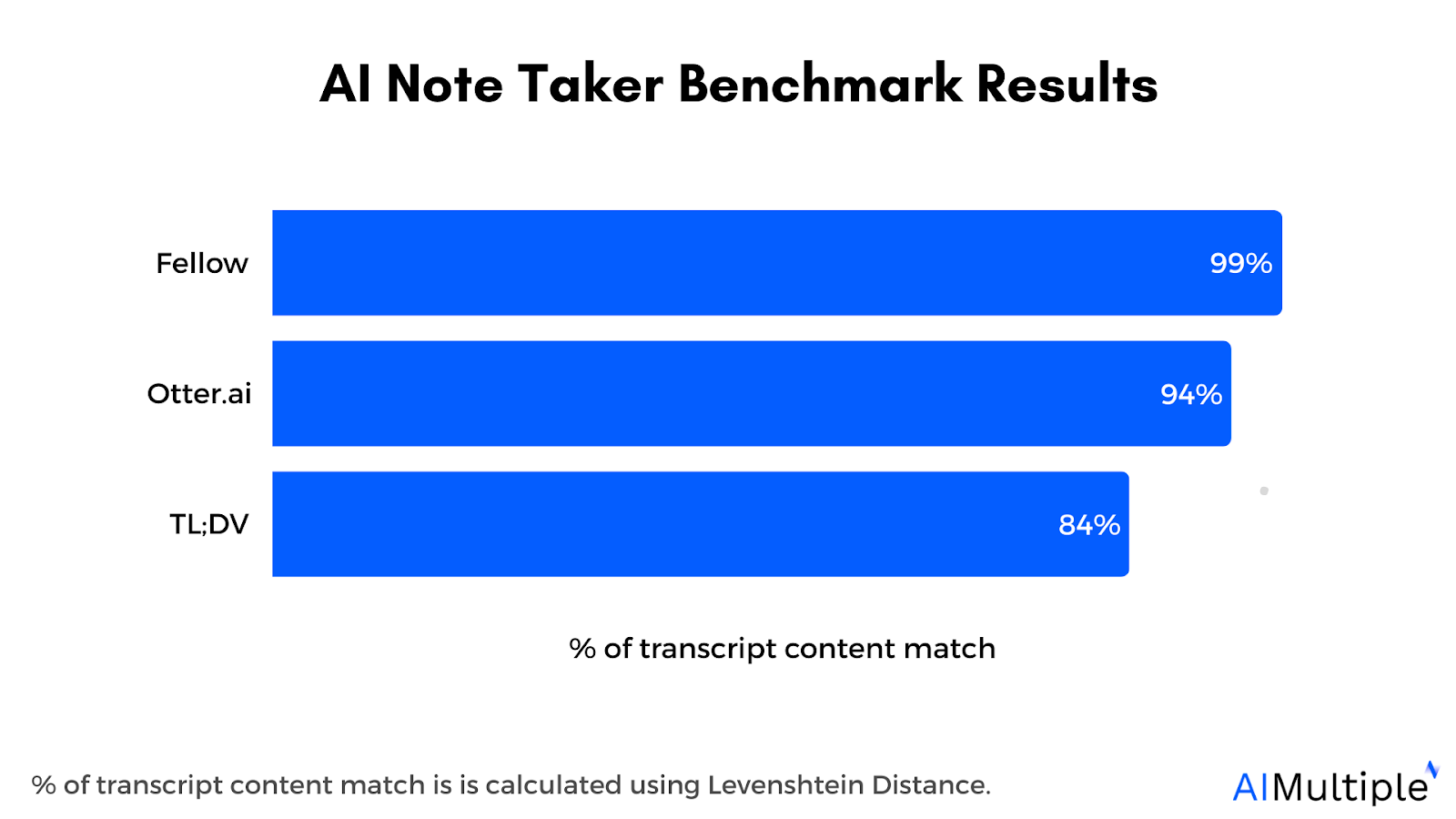
And if you're curious about performance, take a look at the benchmarks results — compared against other popular triangulation libraries.










































































































































































![[The AI Show Episode 146]: Rise of “AI-First” Companies, AI Job Disruption, GPT-4o Update Gets Rolled Back, How Big Consulting Firms Use AI, and Meta AI App](https://www.marketingaiinstitute.com/hubfs/ep%20146%20cover.png)
























































































































![[FREE EBOOKS] Offensive Security Using Python, Learn Computer Forensics — 2nd edition & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![Ditching a Microsoft Job to Enter Startup Purgatory with Lonewolf Engineer Sam Crombie [Podcast #171]](https://cdn.hashnode.com/res/hashnode/image/upload/v1746753508177/0cd57f66-fdb0-4972-b285-1443a7db39fc.png?#)

























































































































































































































-xl.jpg)













![As Galaxy Watch prepares a major change, which smartwatch design to you prefer? [Poll]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2024/07/Galaxy-Watch-Ultra-and-Apple-Watch-Ultra-1.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)












![Beats Studio Buds + On Sale for $99.95 [Lowest Price Ever]](https://www.iclarified.com/images/news/96983/96983/96983-640.jpg)

![New iPad 11 (A16) On Sale for Just $277.78! [Lowest Price Ever]](https://www.iclarified.com/images/news/97273/97273/97273-640.jpg)







































![Apple's 11th Gen iPad Drops to New Low Price of $277.78 on Amazon [Updated]](https://images.macrumors.com/t/yQCVe42SNCzUyF04yj1XYLHG5FM=/2500x/article-new/2025/03/11th-gen-ipad-orange.jpeg)



![[Exclusive] Infinix GT DynaVue: a Prototype that could change everything!](https://www.gizchina.com/wp-content/uploads/images/2025/05/Screen-Shot-2025-05-10-at-16.07.40-PM-copy.png)





![T-Mobile discontinues a free number feature but a paid alternative exists [UPDATED]](https://m-cdn.phonearena.com/images/article/170235-two/T-Mobile-discontinues-a-free-number-feature-but-a-paid-alternative-exists-UPDATED.jpg?#)