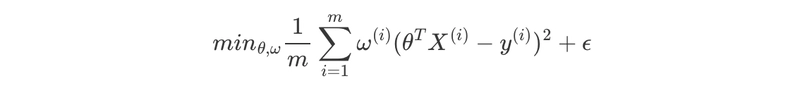LWR in Machine Learning
LWR in Machine Learning Mathematical theorem and predicting credit card spending with Locally Weighted Regression (LWR) We’ll explore Locally Weighted Regression in this chapter. LWR Locally Weighted Regression (LWR) is a non-parametric regression technique that fits a linear regression model to a dataset by weighting neighboring data points more heavily. As LWR learns a local set of parameters for each prediction, LWR can capture non-linear relationships in the data. LWR approx. non-linear function. Image source: Research Gate Key Differences from Linear Regression: LWR has advantages in approximating non-linear function by using local neighborhood to the query point. Yet, it is not the best for addressing larger dataset due to its computational cost, or high-dimensional cost functions as the local neighborhood of given query points might not contain sufficient data points truly close to all dimensions. Comparison of Linear Regression vs LWR Mathematical Theorem LWR has same objectives as linear regression, finding parameters θ that can minimize loss function (1). Yet, its core idea is to assign weights to training points based on their proximity to a query point using weight (ω) based on Gaussian kernel controlled by a bandwidth parameter (τ): The weight: ω denotes (2): where * x(i): a random training example, * x: a given query point and, *

LWR in Machine Learning
Mathematical theorem and predicting credit card spending with Locally Weighted Regression (LWR)
We’ll explore Locally Weighted Regression in this chapter.
LWR
Locally Weighted Regression (LWR) is a non-parametric regression technique that fits a linear regression model to a dataset by weighting neighboring data points more heavily.
As LWR learns a local set of parameters for each prediction, LWR can capture non-linear relationships in the data.
LWR approx. non-linear function. Image source: Research Gate
Key Differences from Linear Regression:
LWR has advantages in approximating non-linear function by using local neighborhood to the query point.
Yet, it is not the best for addressing larger dataset due to its computational cost, or high-dimensional cost functions as the local neighborhood of given query points might not contain sufficient data points truly close to all dimensions.
Comparison of Linear Regression vs LWR
Mathematical Theorem
LWR has same objectives as linear regression, finding parameters θ that can minimize loss function (1).
Yet, its core idea is to assign weights to training points based on their proximity to a query point using weight (ω) based on Gaussian kernel controlled by a bandwidth parameter (τ):
The weight: ω denotes (2):
where
- * x(i): a random training example,
- * x: a given query point and,
- *








































































































































































![[The AI Show Episode 146]: Rise of “AI-First” Companies, AI Job Disruption, GPT-4o Update Gets Rolled Back, How Big Consulting Firms Use AI, and Meta AI App](https://www.marketingaiinstitute.com/hubfs/ep%20146%20cover.png)

























































































































![[FREE EBOOKS] Offensive Security Using Python, Learn Computer Forensics — 2nd edition & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![Ditching a Microsoft Job to Enter Startup Purgatory with Lonewolf Engineer Sam Crombie [Podcast #171]](https://cdn.hashnode.com/res/hashnode/image/upload/v1746753508177/0cd57f66-fdb0-4972-b285-1443a7db39fc.png?#)



























































































































































































































-xl.jpg)













![As Galaxy Watch prepares a major change, which smartwatch design to you prefer? [Poll]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2024/07/Galaxy-Watch-Ultra-and-Apple-Watch-Ultra-1.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)













![Apple M4 iMac Drops to New All-Time Low Price of $1059 [Deal]](https://www.iclarified.com/images/news/97281/97281/97281-640.jpg)
![Beats Studio Buds + On Sale for $99.95 [Lowest Price Ever]](https://www.iclarified.com/images/news/96983/96983/96983-640.jpg)

![New iPad 11 (A16) On Sale for Just $277.78! [Lowest Price Ever]](https://www.iclarified.com/images/news/97273/97273/97273-640.jpg)






































![Apple's 11th Gen iPad Drops to New Low Price of $277.78 on Amazon [Updated]](https://images.macrumors.com/t/yQCVe42SNCzUyF04yj1XYLHG5FM=/2500x/article-new/2025/03/11th-gen-ipad-orange.jpeg)



![[Exclusive] Infinix GT DynaVue: a Prototype that could change everything!](https://www.gizchina.com/wp-content/uploads/images/2025/05/Screen-Shot-2025-05-10-at-16.07.40-PM-copy.png)