The Power of Graphs: From Social Network Analysis to Disease Tracking

Ever wonder how Facebook knows who your mutual friends are, or how Google Maps finds the fastest route through a maze of streets? The secret lies in the elegant and surprisingly powerful world of graphs - a way of seeing connections that's transforming everything from social lives to fighting pandemics. In today's more connected world, relationships and connections are everything. From the social web of interactions to the complicated routes of disease transmission and the most efficient routes of our daily travel, patterns exist that can be best explained by the study of graphs. This blog explores the interesting realm of graph theory, its basic concepts, different representations in computer science, and its influential applications in various fields. Introduction to Graphs Fundamentally, a graph is a mathematical object employed to describe relationships among objects. It is made up of: Nodes (or Vertices): These are the objects or entities in our system. Consider individuals in a social network, cities on a map, or genes in a biological pathway. Edges: These are the relations or links among the nodes. These may be friendships, roads linking cities, or protein-protein interactions. Graph: A DSA Perspective From the Data Structures and Algorithms (DSA) viewpoint, representing and working with graphs efficiently is important. There are several popular representations, each having its own performance vs. space trade-offs depending on the operation. Adjacency List Representation: An adjacency list depicts a graph as an array (or a hash map) of lists. The array index represents a node, and the list at that index comprises all the nodes directly linked to the current node (its neighbors). class GraphAdjList: def init(self, num_vertices): self.num_vertices = num_vertices self.adj_list = [[] for _ in range(num_vertices)] def add_edge(self, u, v): self.adj_list[u].append(v) self.adj_list[v].append(u) # For an undirected graph def str(self): representation = "" for i in range(self.num_vertices): representation += f"{i}: {self.adj_list[i]}\n" return representation # Example usage g_adj_list = GraphAdjList(5) g_adj_list.add_edge(0, 1) g_adj_list.add_edge(0, 4) g_adj_list.add_edge(1, 2) g_adj_list.add_edge(1, 3) g_adj_list.add_edge(1, 4) g_adj_list.add_edge(2, 3) g_adj_list.add_edge(3, 4) print(g_adj_list) Adjacency Matrix Representation: An adjacency matrix is a 2D array (or matrix) where both rows and columns represent the nodes of the graph. An entry at matrix[i][j] is typically 1 (or True) if there is an edge between node i and node j, and 0 (or False) otherwise. For weighted graphs, the weight of the edge can be stored instead of 1. class GraphAdjMatrix: def init(self, num_vertices): self.num_vertices = num_vertices self.adj_matrix = [[0] * num_vertices for _ in range(num_vertices)] def add_edge(self, u, v): self.adj_matrix[u][v] = 1 self.adj_matrix[v][u] = 1 # For an undirected graph def str(self): representation = "" for row in self.adj_matrix: representation += f"{row}\n" return representation # Example usage g_adj_matrix = GraphAdjMatrix(5) g_adj_matrix.add_edge(0, 1) g_adj_matrix.add_edge(0, 4) g_adj_matrix.add_edge(1, 2) g_adj_matrix.add_edge(1, 3) g_adj_matrix.add_edge(1, 4) g_adj_matrix.add_edge(2, 3) g_adj_matrix.add_edge(3, 4) print(g_adj_matrix) Edge List Representation: An edge list is a basic representation which keeps a list of all the edges in the graph. Every entry in the list usually describes an edge as a pair of nodes it is connecting. In weighted graphs, the weight may be added as a third item in the tuple. class GraphEdgeList: def init(self): self.edges = [] def add_edge(self, u, v): self.edges.append((u, v)) def str(self): return f"Edges: {self.edges}" # Example usage g_edge_list = GraphEdgeList() g_edge_list.add_edge(0, 1) g_edge_list.add_edge(0, 4) g_edge_list.add_edge(1, 2) g_edge_list.add_edge(1, 3) g_edge_list.add_edge(1, 4) g_edge_list.add_edge(2, 3) g_edge_list.add_edge(3, 4) print(g_edge_list) As mentioned earlier, the adjacency matrix is actually a 2D matrix. It's worth repeating its usefulness for some graph operations, like verifying the presence of an edge between two nodes in constant time. But for sparse graphs (graphs with much fewer edges than the maximum number possible), the adjacency matrix can be wasteful in terms of memory. Applications The strength of graphs lies in their multifaceted use in different areas. 1. Social Network Analysis Social networks like Facebook, Twitter, and LinkedIn are simply huge graphs with users as nodes and friendships (follows or messages) as edges. Graph algorithms are applied to: Find Influencers: Employing centrality measures such as

Apr 5, 2025 - 15:18

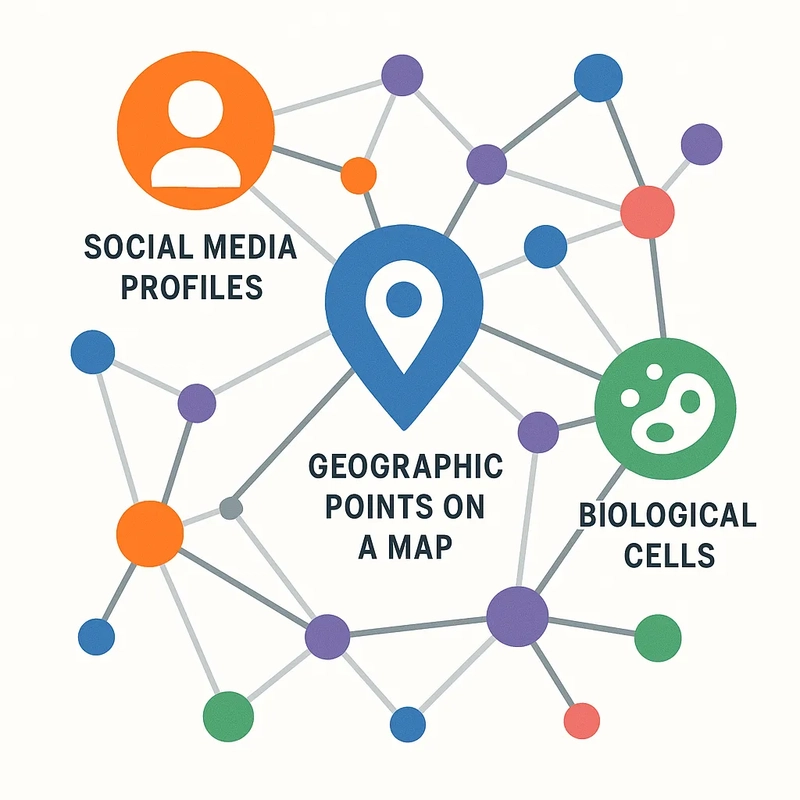
The Power of Graphs: From Social Network Analysis to Disease Tracking

Ever wonder how Facebook knows who your mutual friends are, or how Google Maps finds the fastest route through a maze of streets? The secret lies in the elegant and surprisingly powerful world of graphs - a way of seeing connections that's transforming everything from social lives to fighting pandemics.

In today's more connected world, relationships and connections are everything. From the social web of interactions to the complicated routes of disease transmission and the most efficient routes of our daily travel, patterns exist that can be best explained by the study of graphs. This blog explores the interesting realm of graph theory, its basic concepts, different representations in computer science, and its influential applications in various fields.

Introduction to Graphs

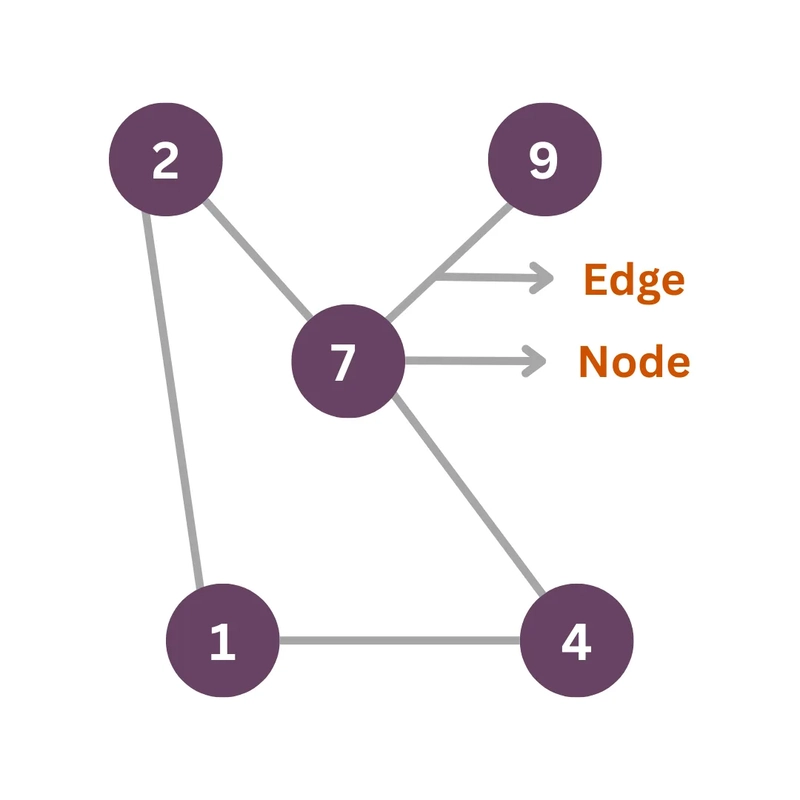
Fundamentally, a graph is a mathematical object employed to describe relationships among objects. It is made up of:

Nodes (or Vertices): These are the objects or entities in our system. Consider individuals in a social network, cities on a map, or genes in a biological pathway.

Edges: These are the relations or links among the nodes. These may be friendships, roads linking cities, or protein-protein interactions.

Graph: A DSA Perspective

From the Data Structures and Algorithms (DSA) viewpoint, representing and working with graphs efficiently is important. There are several popular representations, each having its own performance vs. space trade-offs depending on the operation.

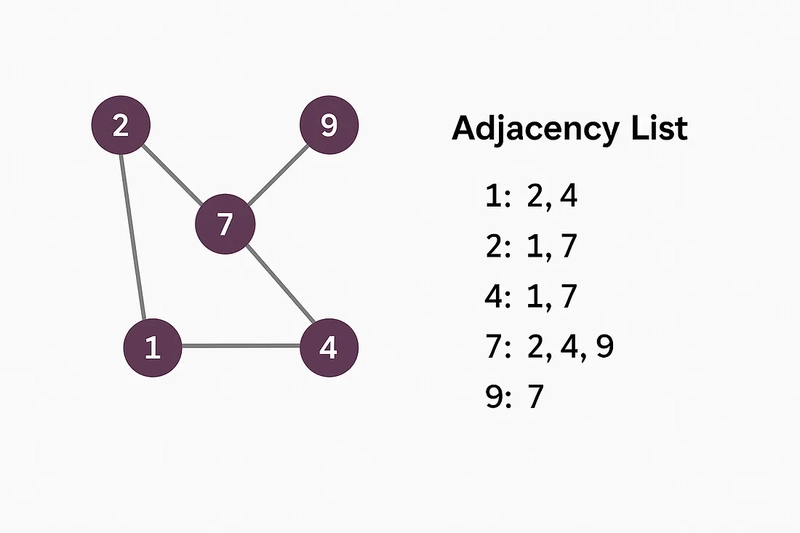
Adjacency List
Representation: An adjacency list depicts a graph as an array (or a hash map) of lists. The array index represents a node, and the list at that index comprises all the nodes directly linked to the current node (its neighbors).

class GraphAdjList:
    def __init__(self, num_vertices):
        self.num_vertices = num_vertices
        self.adj_list = [[] for _ in range(num_vertices)]

    def add_edge(self, u, v):
        self.adj_list[u].append(v)
        self.adj_list[v].append(u) # For an undirected graph

    def __str__(self):
        representation = ""
        for i in range(self.num_vertices):
            representation += f"{i}: {self.adj_list[i]}\n"
        return representation

# Example usage
g_adj_list = GraphAdjList(5)
g_adj_list.add_edge(0, 1)
g_adj_list.add_edge(0, 4)
g_adj_list.add_edge(1, 2)
g_adj_list.add_edge(1, 3)
g_adj_list.add_edge(1, 4)
g_adj_list.add_edge(2, 3)
g_adj_list.add_edge(3, 4)
print(g_adj_list)

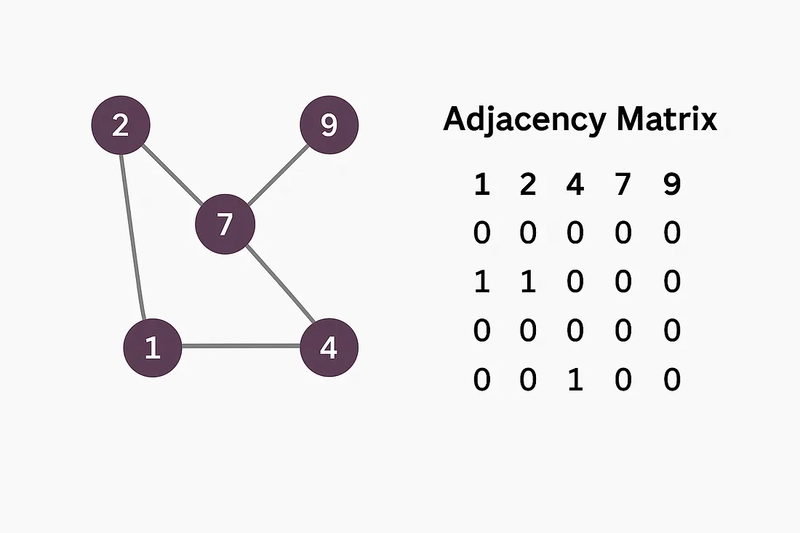
Adjacency Matrix
Representation: An adjacency matrix is a 2D array (or matrix) where both rows and columns represent the nodes of the graph. An entry at matrix[i][j] is typically 1 (or True) if there is an edge between node i and node j, and 0 (or False) otherwise. For weighted graphs, the weight of the edge can be stored instead of 1.

class GraphAdjMatrix:
    def __init__(self, num_vertices):
        self.num_vertices = num_vertices
        self.adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]

    def add_edge(self, u, v):
        self.adj_matrix[u][v] = 1
        self.adj_matrix[v][u] = 1 # For an undirected graph

    def __str__(self):
        representation = ""
        for row in self.adj_matrix:
            representation += f"{row}\n"
        return representation

# Example usage
g_adj_matrix = GraphAdjMatrix(5)
g_adj_matrix.add_edge(0, 1)
g_adj_matrix.add_edge(0, 4)
g_adj_matrix.add_edge(1, 2)
g_adj_matrix.add_edge(1, 3)
g_adj_matrix.add_edge(1, 4)
g_adj_matrix.add_edge(2, 3)
g_adj_matrix.add_edge(3, 4)
print(g_adj_matrix)

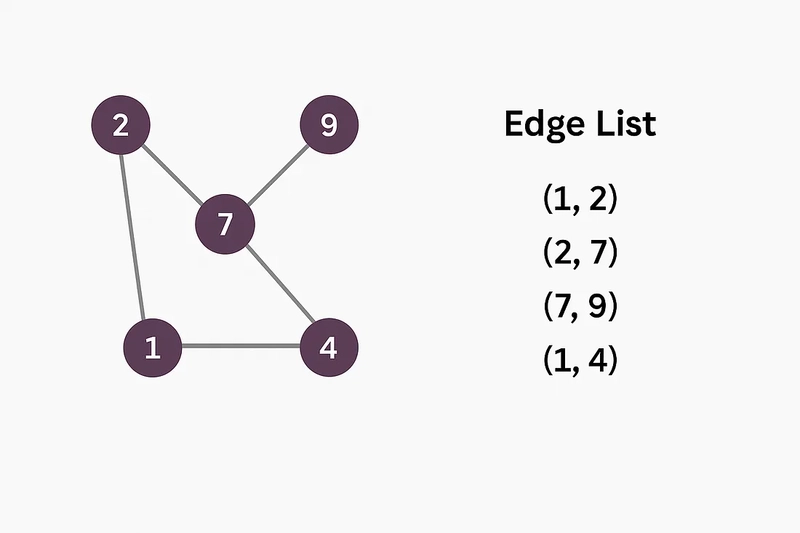
Edge List
Representation: An edge list is a basic representation which keeps a list of all the edges in the graph. Every entry in the list usually describes an edge as a pair of nodes it is connecting. In weighted graphs, the weight may be added as a third item in the tuple.

class GraphEdgeList:
    def __init__(self):
        self.edges = []

    def add_edge(self, u, v):
        self.edges.append((u, v))

    def __str__(self):
        return f"Edges: {self.edges}"

# Example usage
g_edge_list = GraphEdgeList()
g_edge_list.add_edge(0, 1)
g_edge_list.add_edge(0, 4)
g_edge_list.add_edge(1, 2)
g_edge_list.add_edge(1, 3)
g_edge_list.add_edge(1, 4)
g_edge_list.add_edge(2, 3)
g_edge_list.add_edge(3, 4)
print(g_edge_list)

As mentioned earlier, the adjacency matrix is actually a 2D matrix. It's worth repeating its usefulness for some graph operations, like verifying the presence of an edge between two nodes in constant time. But for sparse graphs (graphs with much fewer edges than the maximum number possible), the adjacency matrix can be wasteful in terms of memory.

Applications

The strength of graphs lies in their multifaceted use in different areas.

1. Social Network Analysis

Social networks like Facebook, Twitter, and LinkedIn are simply huge graphs with users as nodes and friendships (follows or messages) as edges. Graph algorithms are applied to:

Find Influencers: Employing centrality measures such as PageRank (famously utilized by Google for web page ranking based on link structure) or Betweenness Centrality (calculating how many times a node occurs on the shortest path between other nodes), we can find the most influential individuals within a network.

Community Detection: Methods such as Girvan-Newman (removes edges with the most betweenness centrality iteratively) or the Louvain Method (a greedy algorithm that finds modularity iteratively) assist in the detection of clusters or communities in a network, identifying groups of users with densely internal connections.

Recommendation Systems: By computing user interactions as a graph, sites can recommend friends, groups, or content based on the activities and connections of nearby users. This utilizes the fact that connected users tend to have similar interests.

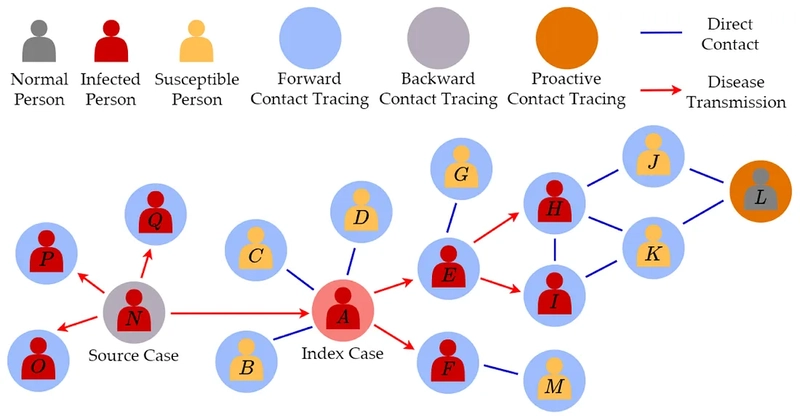
2. Disease Tracking and Epidemic Modeling

Graphs are essential in disease spread modeling. For instance:

Contact Tracing: In the COVID-19 outbreak, graphs have been used to model contact networks where nodes are individuals and edges are interactions. Breadth-First Search (BFS) algorithms were used to find all the people who interacted with an infected individual, making it possible to efficiently conduct contact tracing.

Epidemic Thresholds: Through graph-based models, scientists can make predictions about the speed with which a disease spreads using the network configuration and characteristics such as the average number of contacts for an individual. This informs the critical threshold of herd immunity and is used to guide public health interventions.

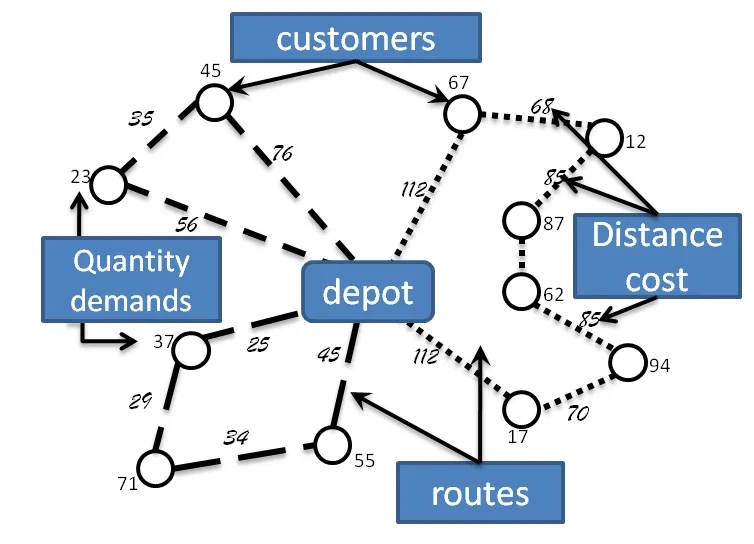
3. Transportation and Routing

Graph algorithms form the crux of map navigation systems such as Google Maps. For example:

Shortest Path Algorithms: Dijkstra's and A* algorithms are used to determine the quickest or shortest path between two points, keeping in mind such factors as travel time and distance.

Traffic Optimization: By representing cities as graphs, intersections as nodes, and roads as edges (possibly weighted by traffic levels), traffic can be modeled and optimized to decrease congestion and increase efficiency.

Graph Algorithms in Action

Some of the basic graph algorithms drive these uses:

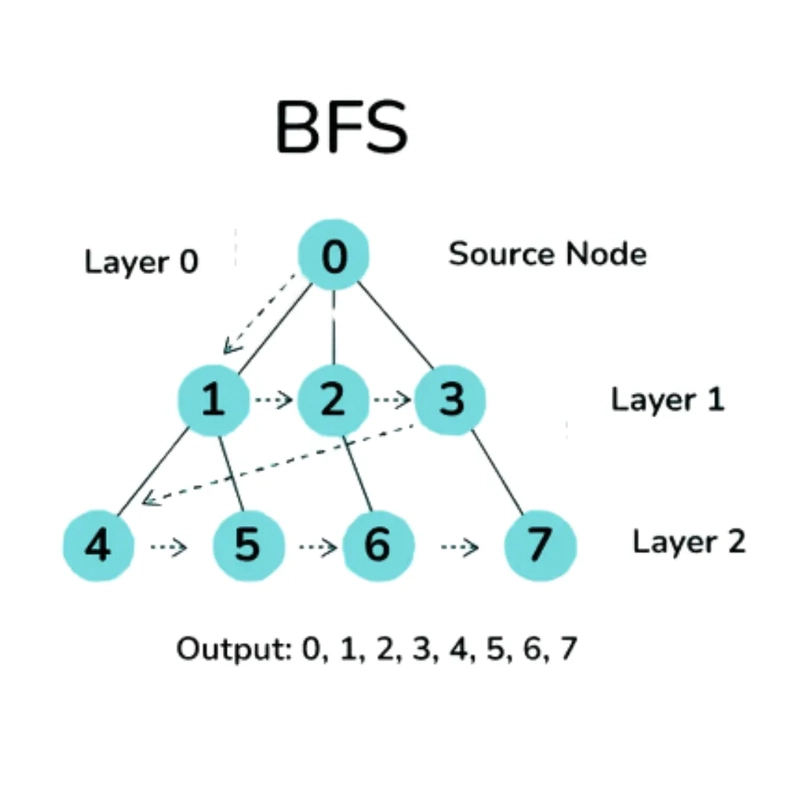
1. Breadth-First Search (BFS): Traverses a graph level by level.

Applied to: Social networks to determine the shortest path (number of connections) between users.
Used in: Disease tracing to find all the people who have been in contact with an infected person within a given number of contacts.

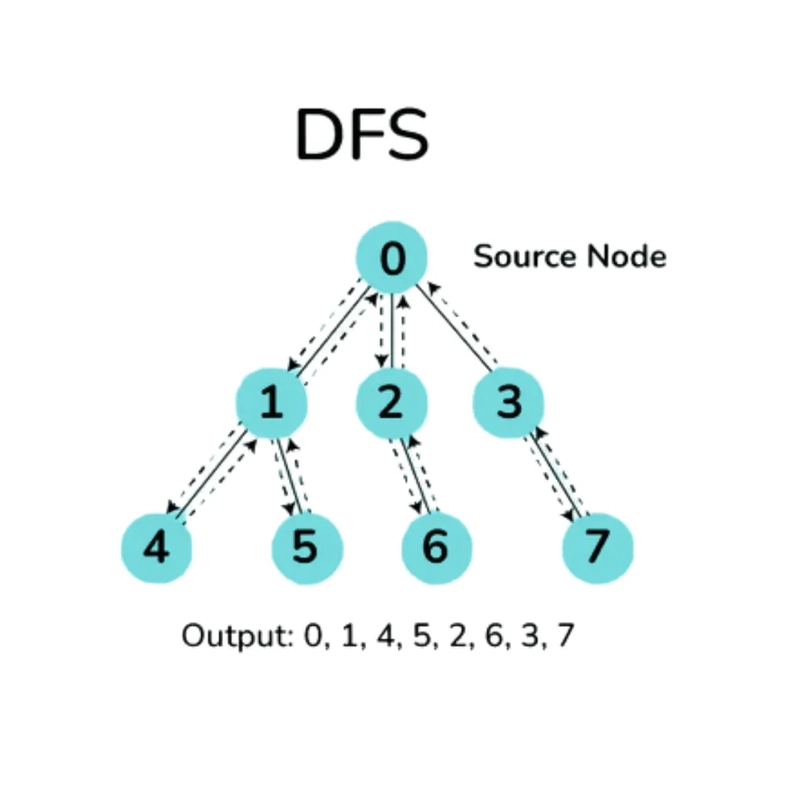
2. Depth-First Search (DFS): Travels as far as possible along each branch before backtracking.

Assists in detecting: Cycles in dependency graphs, e.g., course prerequisites or software dependencies (if there is a cycle, it means there is a circular dependency).
Used in: Puzzle games and maze-solving algorithms where all possible exploration down an avenue is required.

3. Dijkstra's Algorithm: Determines the shortest path from one source node to all other nodes in a graph with non-negative edge weights.

Powers: Navigation systems through finding the shortest paths.
Used in: Network routing algorithms to minimize delivery of data packets according to network delay or cost.

4. Floyd-Warshall Algorithm: Calculates the shortest paths between every pair of nodes in a weighted graph (supports negative edge weights, but not negative cycles).

Used in: Planning deliveries and transportation logistics to find the best routes between several destinations, based on distances or costs between all points.

5. Minimum Spanning Tree (MST) Algorithms (e.g., Kruskal's, Prim's): Determine a subset of the edges that connects all the vertices in a tree structure, with no cycles and minimum total edge weight.

Applied in: Creating cost-effective networks, like electric grids, telecommunication systems, or internet cable configurations, to reduce the expense of installing connections and still have every point be linked.

Future of Graphs

Applications of graph theory keep expanding at a lightning pace.

Graph Neural Networks (GNNs): This burgeoning field brings graph theory and machine learning together in a powerful mix. GNNs can acquire node and graph representations, and thus solutions for hard problems such as drug discovery (predicting molecule interaction), fraud detection (detecting aberrant patterns within financial transaction graphs), and social recommendation with improved contextual insight.

Real-Time Network Analysis: With the deluge of data from dynamic networks such as social media streams and financial transactions, the creation of streaming graph algorithms is essential. The algorithms can track and analyze changing networks in real-time, facilitating timely detection of trends, anomalies, and pivotal events.

Conclusion

Graphs are a robust and flexible way of understanding and modeling the interconnectedness of our world. From the algorithms behind our social media feeds and navigation systems to the models used to track and fight diseases, the "power of graphs" cannot be disputed. As information gets more and more complicated and integrated, graph theory and its algorithmic applications will increasingly become invaluable to tackling the most fundamental and vexing challenges and unleashing new opportunities across a wide array of fields.