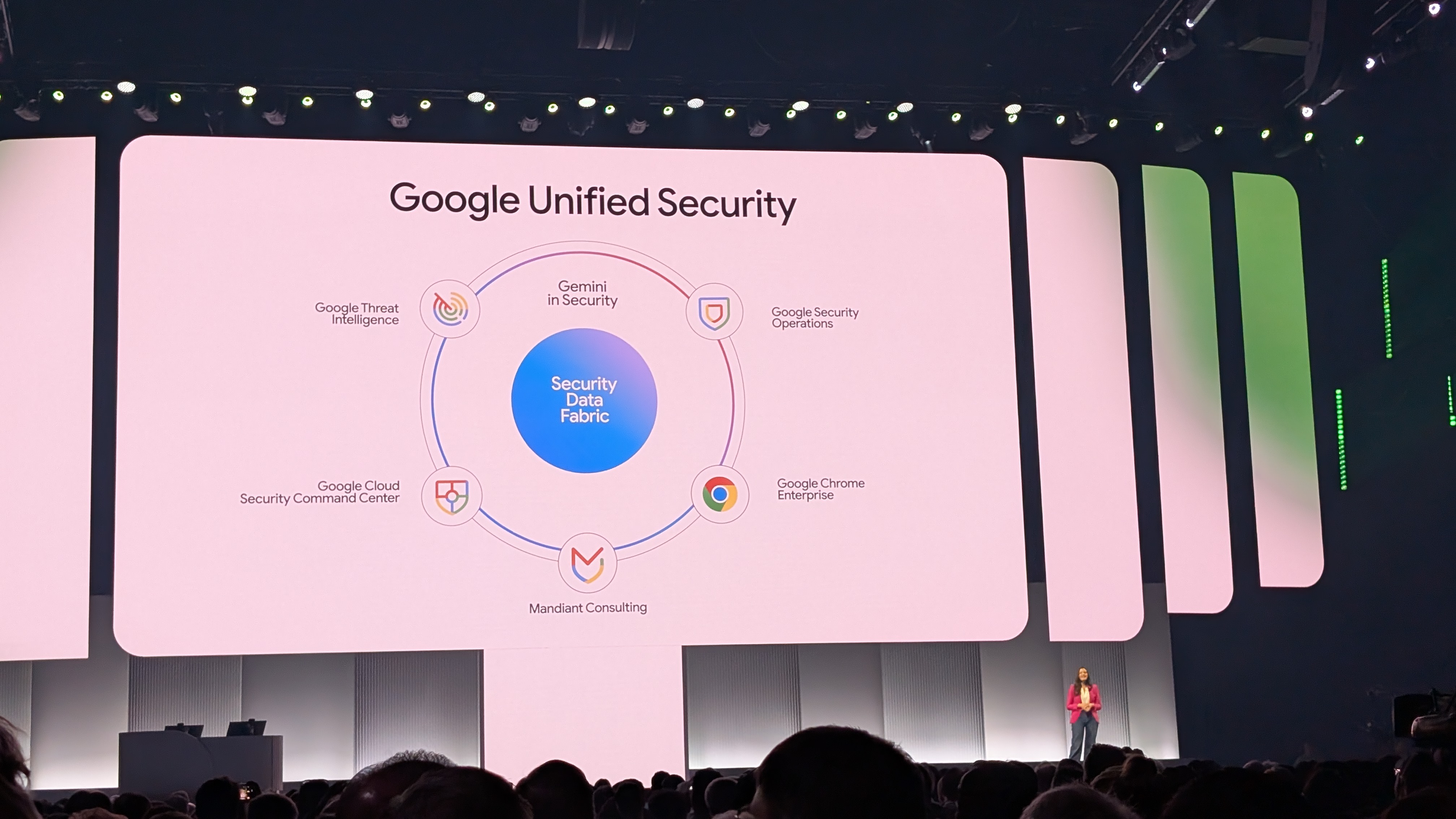
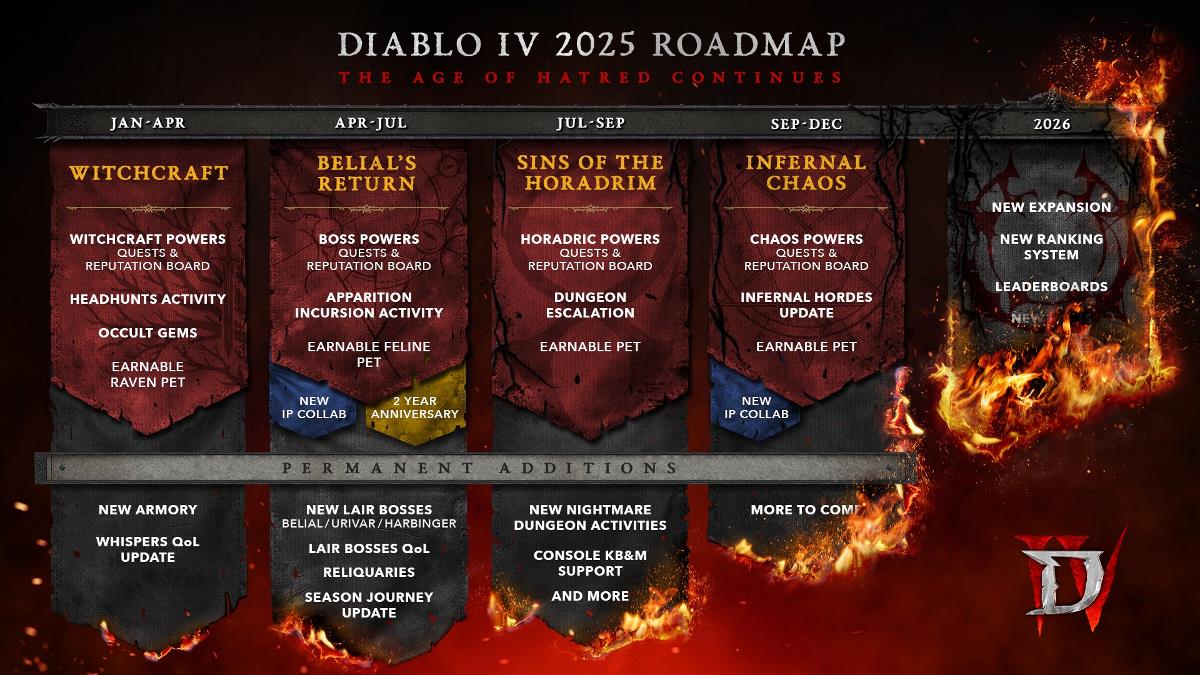
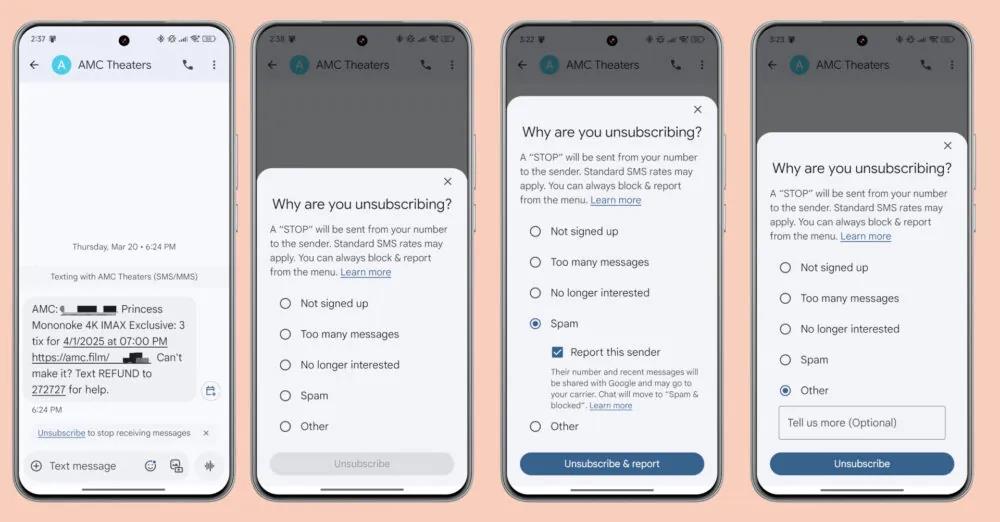
# Subset Sum - Greedy Approach (Not Guaranteed Optimal)
# Description: Attempts to find a subset of numbers that sums exactly to a target value using a greedy strategy.
def subset_sum(nums, target):
"""
Find a subset of numbers that sum exactly to the target using a greedy approach.
This algorithm attempts to construct a subset by selecting numbers
in a way that approaches the target sum. It is not guaranteed to find
a solution even if one exists, due to its greedy nature.
Args:
nums (list of int): List of available numbers to select from.
target (int): The desired total sum.
Returns:
list or str: A subset that sums to the target, or "No solution" if not found.
Key Characteristics:
- Sorts numbers in descending order to prioritize larger numbers
- Greedily selects numbers that don't exceed the target
- Not guaranteed to find a solution for all possible inputs
Time Complexity: O(n log n) due to sorting
Space Complexity: O(n)
Note: This is an approximation and may not work for all subset sum instances.
"""
# Check for invalid or impossible inputs
if target < 0 or not nums:
return "No solution"
# Sort numbers in descending order to prioritize larger numbers
sorted_nums = sorted(nums, reverse=True)
# Attempt to construct a subset
current_subset = []
current_sum = 0
# Greedily select numbers that don't exceed the target
for num in sorted_nums:
# If adding the current number doesn't exceed the target, include it
if current_sum + num <= target:
current_subset.append(num)
current_sum += num
# Early exit if exact target is reached
if current_sum == target:
return current_subset
# Check if an exact solution was found
return current_subset if current_sum == target else "No solution"
# Alternative implementation demonstrating multiple approaches
def subset_sum_advanced(nums, target):
"""
A more comprehensive subset sum solver with multiple strategies.
This version demonstrates additional handling and can be extended
to include more sophisticated search strategies.
Args:
nums (list of int): List of available numbers.
target (int): Desired total sum.
Returns:
list or str: Solutions found through different methods.
"""
def backtrack(index, current_subset, current_sum):
# Found a valid subset
if current_sum == target:
return current_subset
# Exceeded target or reached end of numbers
if current_sum > target or index >= len(nums):
return None
# Try including the current number
with_current = backtrack(
index + 1,
current_subset + [nums[index]],
current_sum + nums[index]
)
if with_current:
return with_current
# Try excluding the current number
without_current = backtrack(
index + 1,
current_subset,
current_sum
)
return without_current
result = backtrack(0, [], 0)
return result if result else "No solution"
# Demonstration function
def demonstrate_subset_sum():
"""
Demonstrate subset sum solving with various inputs.
"""
test_cases = [
([1, 2, 3, 4, 5, 6], 10), # Possible solution
([7, 3, 2, 5], 15), # Another test case
([100, 200, 300], 50) # Impossible case
]
for nums, target in test_cases:
print(f"\nTesting nums={nums}, target={target}")
print("Greedy Approach:", subset_sum(nums, target))
print("Advanced Approach:", subset_sum_advanced(nums, target))







































































































































































![[The AI Show Episode 143]: ChatGPT Revenue Surge, New AGI Timelines, Amazon’s AI Agent, Claude for Education, Model Context Protocol & LLMs Pass the Turing Test](https://www.marketingaiinstitute.com/hubfs/ep%20143%20cover.png)







































































































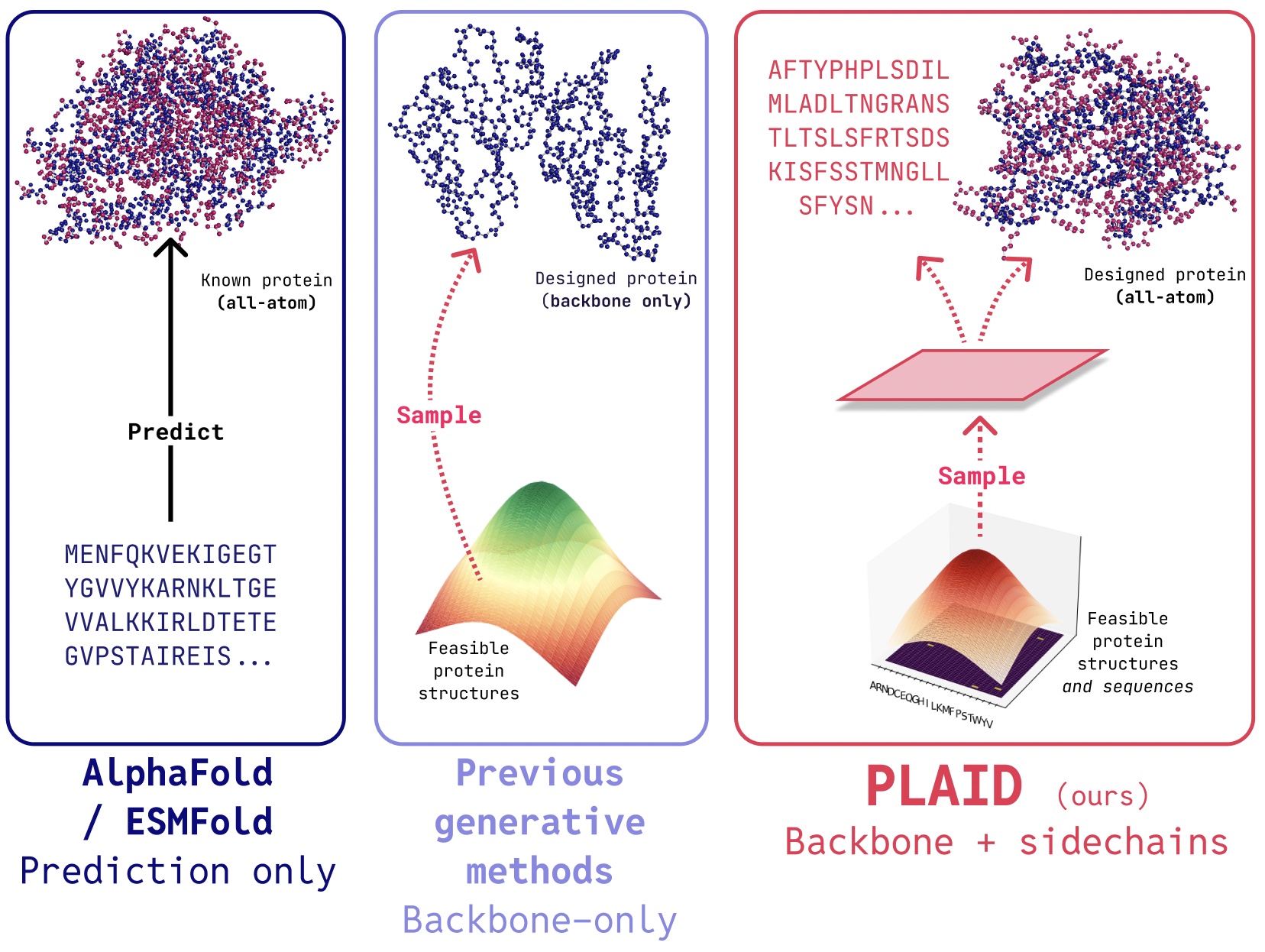

























![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)










































.jpeg?#)

































































-11.11.2024-4-49-screenshot.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)






















_jvphoto_Alamy.jpg?#)





.png?#)

































































































![Apple Debuts Official Trailer for 'Murderbot' [Video]](https://www.iclarified.com/images/news/96972/96972/96972-640.jpg)
![Alleged Case for Rumored iPhone 17 Pro Surfaces Online [Image]](https://www.iclarified.com/images/news/96969/96969/96969-640.jpg)

![Apple Rushes Five Planes of iPhones to US Ahead of New Tariffs [Report]](https://www.iclarified.com/images/news/96967/96967/96967-640.jpg)