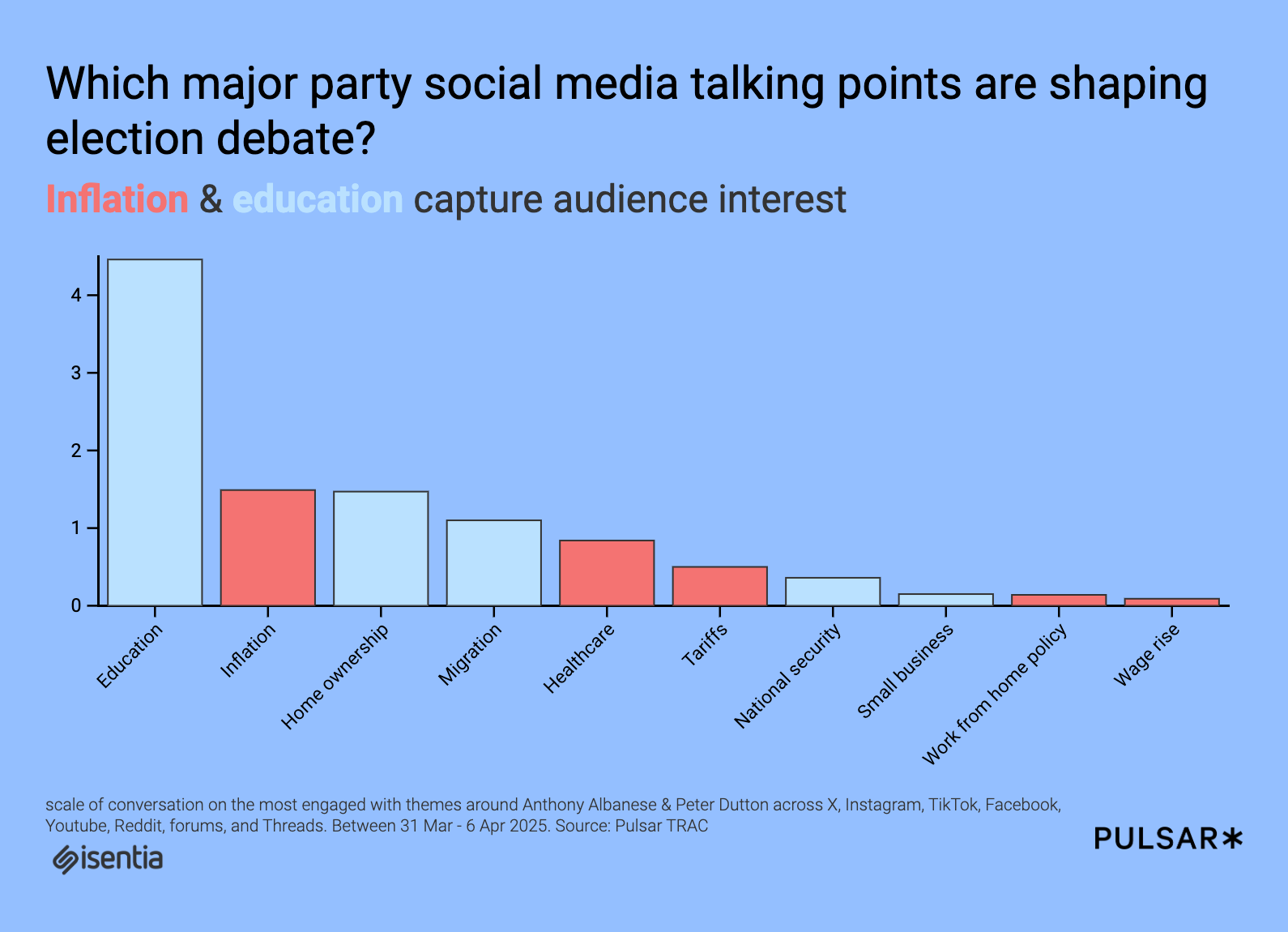
Approximates a minimum Steiner tree by greedily connecting terminals with the shortest edges.
# Steiner Tree - Greedy Approach (Not Optimal) # Description: Approximates a minimum Steiner tree by greedily connecting terminals with the shortest edges. def steiner_tree(graph, terminals): """ Approximates the Steiner Tree using a greedy approach. This algorithm connects terminal nodes by repeatedly adding the shortest edge that connects an existing tree node to a new node. Args: graph (dict): Adjacency list representation with edge weights. terminals (list): Nodes that must be included in the final tree. Returns: set: Nodes in the approximated Steiner tree. Time Complexity: O(V^2), where V is the number of vertices Space Complexity: O(V) Note: This is a greedy approximation and may not find the optimal Steiner tree. """ # Initialize the tree with terminal nodes tree = set(terminals) # Iteratively expand the tree by adding the shortest connecting edge while len(tree) < len(graph): # Find the shortest edge connecting the current tree to a new node shortest_edge = None min_distance = float('inf') # Check edges from each node in the current tree for current_node in tree: for neighbor, distance in graph[current_node].items(): # Find the shortest edge to a node not yet in the tree if neighbor not in tree and distance < min_distance: shortest_edge = (current_node, neighbor) min_distance = distance # If no connecting edge is found, break the loop if shortest_edge is None: break # Add the new node to the tree tree.add(shortest_edge[1]) return tree

# Steiner Tree - Greedy Approach (Not Optimal)
# Description: Approximates a minimum Steiner tree by greedily connecting terminals with the shortest edges.
def steiner_tree(graph, terminals):
"""
Approximates the Steiner Tree using a greedy approach.
This algorithm connects terminal nodes by repeatedly adding the shortest
edge that connects an existing tree node to a new node.
Args:
graph (dict): Adjacency list representation with edge weights.
terminals (list): Nodes that must be included in the final tree.
Returns:
set: Nodes in the approximated Steiner tree.
Time Complexity: O(V^2), where V is the number of vertices
Space Complexity: O(V)
Note: This is a greedy approximation and may not find the optimal Steiner tree.
"""
# Initialize the tree with terminal nodes
tree = set(terminals)
# Iteratively expand the tree by adding the shortest connecting edge
while len(tree) < len(graph):
# Find the shortest edge connecting the current tree to a new node
shortest_edge = None
min_distance = float('inf')
# Check edges from each node in the current tree
for current_node in tree:
for neighbor, distance in graph[current_node].items():
# Find the shortest edge to a node not yet in the tree
if neighbor not in tree and distance < min_distance:
shortest_edge = (current_node, neighbor)
min_distance = distance
# If no connecting edge is found, break the loop
if shortest_edge is None:
break
# Add the new node to the tree
tree.add(shortest_edge[1])
return tree








































































































































































![[The AI Show Episode 143]: ChatGPT Revenue Surge, New AGI Timelines, Amazon’s AI Agent, Claude for Education, Model Context Protocol & LLMs Pass the Turing Test](https://www.marketingaiinstitute.com/hubfs/ep%20143%20cover.png)































































































































![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)






































































































.jpg?#)
































_ArtemisDiana_Alamy.jpg?#)


 (1).webp?#)




































































-xl.jpg)










![Yes, the Gemini icon is now bigger and brighter on Android [U]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2025/02/Gemini-on-Galaxy-S25.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)










![Apple Rushes Five Planes of iPhones to US Ahead of New Tariffs [Report]](https://www.iclarified.com/images/news/96967/96967/96967-640.jpg)
![Apple Vision Pro 2 Allegedly in Production Ahead of 2025 Launch [Rumor]](https://www.iclarified.com/images/news/96965/96965/96965-640.jpg)