2900. Longest Unequal Adjacent Groups Subsequence I
2900. Longest Unequal Adjacent Groups Subsequence I Difficulty: Easy Topics: Array, String, Dynamic Programming, Greedy You are given a string array words and a binary array groups both of length n, where words[i] is associated with groups[i]. Your task is to select the longest alternating subsequence1 from words. A subsequence of words is alternating if for any two consecutive strings in the sequence, their corresponding elements in the binary array groups differ. Essentially, you are to choose strings such that adjacent elements have non-matching corresponding bits in the groups array. Formally, you need to find the longest subsequence of an array of indices [0, 1, ..., n - 1] denoted as [i0, i1, ..., ik-1], such that groups[ij] != groups[ij+1] for each 0
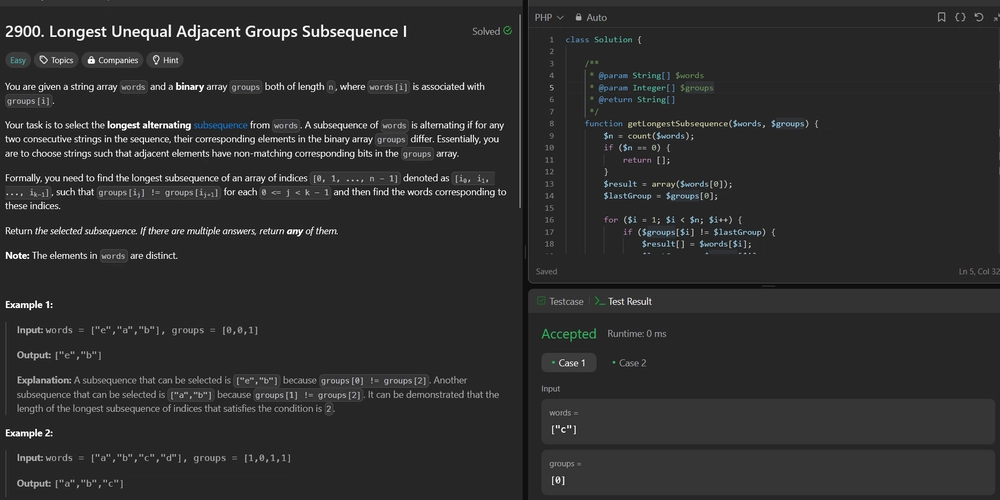
2900. Longest Unequal Adjacent Groups Subsequence I
Difficulty: Easy
Topics: Array, String, Dynamic Programming, Greedy
You are given a string array words and a binary array groups both of length n, where words[i] is associated with groups[i].
Your task is to select the longest alternating subsequence1 from words. A subsequence of words is alternating if for any two consecutive strings in the sequence, their corresponding elements in the binary array groups differ. Essentially, you are to choose strings such that adjacent elements have non-matching corresponding bits in the groups array.
Formally, you need to find the longest subsequence of an array of indices [0, 1, ..., n - 1] denoted as [i0, i1, ..., ik-1], such that groups[ij] != groups[ij+1] for each 0 <= j < k - 1 and then find the words corresponding to these indices.
Return the selected subsequence. If there are multiple answers, return any of them.
Note: The elements in words are distinct.
Example 1:
- Input: words = ["e","a","b"], groups = [0,0,1]
- Output: ["e","b"]
-
Explanation: A subsequence that can be selected is
["e","b"]becausegroups[0] != groups[2]. Another subsequence that can be selected is["a","b"]becausegroups[1] != groups[2]. It can be demonstrated that the length of the longest subsequence of indices that satisfies the condition is2.
Example 2:
- Input: words = ["a","b","c","d"], groups = [1,0,1,1]
- Output: ["a","b","c"]
-
Explanation: A subsequence that can be selected is
["a","b","c"]becausegroups[0] != groups[1]andgroups[1] != groups[2]. Another subsequence that can be selected is["a","b","d"]becausegroups[0] != groups[1]andgroups[1] != groups[3]. It can be shown that the length of the longest subsequence of indices that satisfies the condition is3.
Constraints:
1 <= n == words.length == groups.length <= 1001 <= words[i].length <= 10-
groups[i]is either0or1. -
wordsconsists of distinct strings. -
words[i]consists of lowercase English letters.
Hint:
- This problem can be solved greedily.
- Begin by constructing the answer starting with the first number in
groups. - For each index
iin the range[1, n - 1], addito the answer ifgroups[i] != groups[i - 1].
Solution:
We need to find the longest subsequence of words such that adjacent elements in the subsequence have different corresponding values in the binary array groups. This can be efficiently achieved using a greedy approach.
Approach
The greedy approach works by iterating through the groups array and constructing the subsequence by selecting each element whose group value differs from the previous element in the subsequence. This ensures that we always take the earliest possible elements that allow for the maximum length of alternating groups. Here are the steps:
-
Initialize the Result: Start with the first element from the
wordsarray since it will always be part of the subsequence. - Iterate Through the Array: For each subsequent element, check if its group value is different from the last element added to the result. If it is different, add the current word to the result and update the last group value.
- Return the Result: The constructed subsequence is returned as the answer.
This approach ensures that we build the longest possible alternating subsequence by making locally optimal choices at each step.
Let's implement this solution in PHP: 2900. Longest Unequal Adjacent Groups Subsequence I
/**
* @param String[] $words
* @param Integer[] $groups
* @return String[]
*/
function getLongestSubsequence($words, $groups) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example 1:
$words1 = ["e","a","b"];
$groups1 = [0,0,1];
print_r(getLongestSubsequence($words1, $groups1));
// Example 2:
$words2 = ["a","b","c","d"];
$groups2 = [1,0,1,1];
print_r(getLongestSubsequence($words2, $groups2));
?>
Explanation:
-
Initialization: We start by adding the first word from the
wordsarray to our result list and note its group value. - Iteration: We loop through the remaining elements. For each element, we check if its group value is different from the last group value in our result list. If it is different, we add the current word to the result and update the last group value to the current element's group.
- Result Construction: By following this approach, we ensure that each element added to the result list alternates the group values, thus forming the longest possible subsequence with alternating groups.
This method efficiently constructs the required subsequence in linear time, making it optimal for the given problem constraints.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks





































































































































































![[The AI Show Episode 147]: OpenAI Abandons For-Profit Plan, AI College Cheating Epidemic, Apple Says AI Will Replace Search Engines & HubSpot’s AI-First Scorecard](https://www.marketingaiinstitute.com/hubfs/ep%20147%20cover.png)
























![How to Enable Remote Access on Windows 10 [Allow RDP]](https://bigdataanalyticsnews.com/wp-content/uploads/2025/05/remote-access-windows.jpg)

























































































![[DEALS] The 2025 Ultimate GenAI Masterclass Bundle (87% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)





































































![Legends Reborn tier list of best heroes for each class [May 2025]](https://media.pocketgamer.com/artwork/na-33360-1656320479/pg-magnum-quest-fi-1.jpeg?#)






























































-Olekcii_Mach_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)

_Brian_Jackson_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)






























































































![Top Gear gives us a detailed look at Apple CarPlay Ultra [Video]](https://i0.wp.com/9to5mac.com/wp-content/uploads/sites/6/2025/05/Top-Gear-gives-us-a-first-look-at-Apple-CarPlay-Ultra-Video.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)


![YouTube will use Gemini to insert ads around the parts of a video you care about most [Video]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2025/05/gemini-youtube-ads-1.png?resize=1200%2C628&quality=82&strip=all&ssl=1)
















![Trump Tells Cook to Stop Building iPhones in India and Build in the U.S. Instead [Video]](https://www.iclarified.com/images/news/97329/97329/97329-640.jpg)