ElasticFourierTransformer: Probabilistic Token Mapping via Learned Centroids

Abstract We present ElasticFourierTransformer, a novel neural architecture that learns to embed tokens in a semantic space where natural language concepts are represented as centroids in a continuous embedding space. Unlike traditional language models that map directly from context to token probabilities, our approach separates these tasks: it first maps context to "concept centroids" in embedding space, then maps these centroids to probabilistic token distributions. This separation enables more flexible, interpretable language modeling that captures semantic relationships between tokens while maintaining high precision. We demonstrate that our model discovers meaningful linguistic patterns beyond its explicit training objective, exhibiting properties of emergent semantic organization without explicit supervision. 1. Introduction Large language models typically model token probabilities directly via next-token prediction. While effective, this approach lacks interpretability and can be brittle when confronted with semantic ambiguity. We propose an alternative two-stage approach: First, map input context to a semantically meaningful location in a continuous embedding space Then, interpret this location with respect to nearby "concept centroids" to produce token probabilities This decoupling provides several advantages: improved interpretability of model decisions, more robust handling of semantic ambiguity, and a more natural representation of the many-to-many relationships between words and concepts. Our key contributions include: A novel transformer architecture utilizing elastic Fourier and wave-based components A distance-based clustering approach that organizes tokens into semantic centroids A probabilistic token mapping system that handles the many-to-many relationship between tokens and concepts Evidence that our model discovers meaningful linguistic patterns and conceptual organization beyond its explicit training objective 2. Model Architecture 2.1 ElasticFourierTransformer The core of our approach is the ElasticFourierTransformer, which replaces traditional attention mechanisms with elastic Fourier units and wave-based transformations. 2.1.1 ElasticFourierUnit class ElasticFourierUnit(nn.Module): def init(self, dim, modes=4): super().init() self.dim = dim self.modes = modes # Learnable frequency coefficients self.freqs = nn.Parameter(torch.randn(dim, modes) * 0.02) # Learnable phase shifts self.phases = nn.Parameter(torch.randn(dim, modes) * 0.02) # Learnable amplitudes self.amplitudes = nn.Parameter(torch.ones(dim, modes) * 0.5) This unit performs spectral transformation with learnable parameters, enabling the model to capture periodic patterns in the data. Rather than relying on fixed Fourier basis functions, our unit learns optimal frequency components for the task. 2.1.2 Elastic3dWaveUnit This component models interactions in embedding space using wave equations with learnable parameters: class Elastic3dWaveUnit(nn.Module): def init(self, dim, complexity=3): super().init() self.dim = dim self.complexity = complexity # Learnable wave parameters self.freq_spatial = nn.Parameter(torch.randn(dim, complexity) * 0.02) self.phase_spatial = nn.Parameter(torch.randn(dim, complexity) * 0.02) self.amp_spatial = nn.Parameter(torch.ones(dim, complexity) * 0.5) This creates a more flexible attention mechanism that can capture complex spatial relationships in token embeddings. 2.1.3 ElasticFourierAttention Our attention mechanism replaces the traditional dot-product attention with a wave-based transformation that maintains context awareness: class ElasticFourierAttention(nn.Module): def init(self, dim, heads=4, complexity=3, activation='silu'): super().init() self.dim = dim # Replace traditional attention with Elastic3dWaveUnit self.wave_unit = Elastic3dWaveUnit(dim, complexity=complexity*heads) # Add a context mixer self.context_mixer = nn.Linear(dim, dim) # Learnable sequence gating self.seq_gating = nn.Parameter(torch.zeros(1, 1, dim)) This approach replaces the quadratic complexity of standard attention with a more efficient wave-based transformation while preserving context awareness. 2.2 Tribit Encoding Rather than working with discrete token IDs directly, we represent tokens using "tribit" encoding—vectors of ternary values (-1, 0, 1). This representation provides: Smoother embedding space that better captures semantic gradients More efficient representation than one-hot encoding Natural handling of uncertainty in token predictions Enables representation of conceptual "in-betweenness" of tokens Our training dataset consists of tribit-encoded toke

Apr 29, 2025 - 19:16

ElasticFourierTransformer: Probabilistic Token Mapping via Learned Centroids

Abstract

We present ElasticFourierTransformer, a novel neural architecture that learns to embed tokens in a semantic space where natural language concepts are represented as centroids in a continuous embedding space. Unlike traditional language models that map directly from context to token probabilities, our approach separates these tasks: it first maps context to "concept centroids" in embedding space, then maps these centroids to probabilistic token distributions. This separation enables more flexible, interpretable language modeling that captures semantic relationships between tokens while maintaining high precision. We demonstrate that our model discovers meaningful linguistic patterns beyond its explicit training objective, exhibiting properties of emergent semantic organization without explicit supervision.

1. Introduction

Large language models typically model token probabilities directly via next-token prediction. While effective, this approach lacks interpretability and can be brittle when confronted with semantic ambiguity. We propose an alternative two-stage approach:

First, map input context to a semantically meaningful location in a continuous embedding space
Then, interpret this location with respect to nearby "concept centroids" to produce token probabilities

This decoupling provides several advantages: improved interpretability of model decisions, more robust handling of semantic ambiguity, and a more natural representation of the many-to-many relationships between words and concepts.

Our key contributions include:

A novel transformer architecture utilizing elastic Fourier and wave-based components
A distance-based clustering approach that organizes tokens into semantic centroids
A probabilistic token mapping system that handles the many-to-many relationship between tokens and concepts
Evidence that our model discovers meaningful linguistic patterns and conceptual organization beyond its explicit training objective

2. Model Architecture

2.1 ElasticFourierTransformer

The core of our approach is the ElasticFourierTransformer, which replaces traditional attention mechanisms with elastic Fourier units and wave-based transformations.

2.1.1 ElasticFourierUnit

class ElasticFourierUnit(nn.Module):
    def __init__(self, dim, modes=4):
        super().__init__()
        self.dim = dim
        self.modes = modes

        # Learnable frequency coefficients
        self.freqs = nn.Parameter(torch.randn(dim, modes) * 0.02)
        # Learnable phase shifts
        self.phases = nn.Parameter(torch.randn(dim, modes) * 0.02)
        # Learnable amplitudes
        self.amplitudes = nn.Parameter(torch.ones(dim, modes) * 0.5)

This unit performs spectral transformation with learnable parameters, enabling the model to capture periodic patterns in the data. Rather than relying on fixed Fourier basis functions, our unit learns optimal frequency components for the task.

2.1.2 Elastic3dWaveUnit

This component models interactions in embedding space using wave equations with learnable parameters:

class Elastic3dWaveUnit(nn.Module):
    def __init__(self, dim, complexity=3):
        super().__init__()
        self.dim = dim
        self.complexity = complexity

        # Learnable wave parameters
        self.freq_spatial = nn.Parameter(torch.randn(dim, complexity) * 0.02)
        self.phase_spatial = nn.Parameter(torch.randn(dim, complexity) * 0.02)
        self.amp_spatial = nn.Parameter(torch.ones(dim, complexity) * 0.5)

This creates a more flexible attention mechanism that can capture complex spatial relationships in token embeddings.

2.1.3 ElasticFourierAttention

Our attention mechanism replaces the traditional dot-product attention with a wave-based transformation that maintains context awareness:

class ElasticFourierAttention(nn.Module):
    def __init__(self, dim, heads=4, complexity=3, activation='silu'):
        super().__init__()
        self.dim = dim
        # Replace traditional attention with Elastic3dWaveUnit
        self.wave_unit = Elastic3dWaveUnit(dim, complexity=complexity*heads)
        # Add a context mixer
        self.context_mixer = nn.Linear(dim, dim)
        # Learnable sequence gating
        self.seq_gating = nn.Parameter(torch.zeros(1, 1, dim))

This approach replaces the quadratic complexity of standard attention with a more efficient wave-based transformation while preserving context awareness.

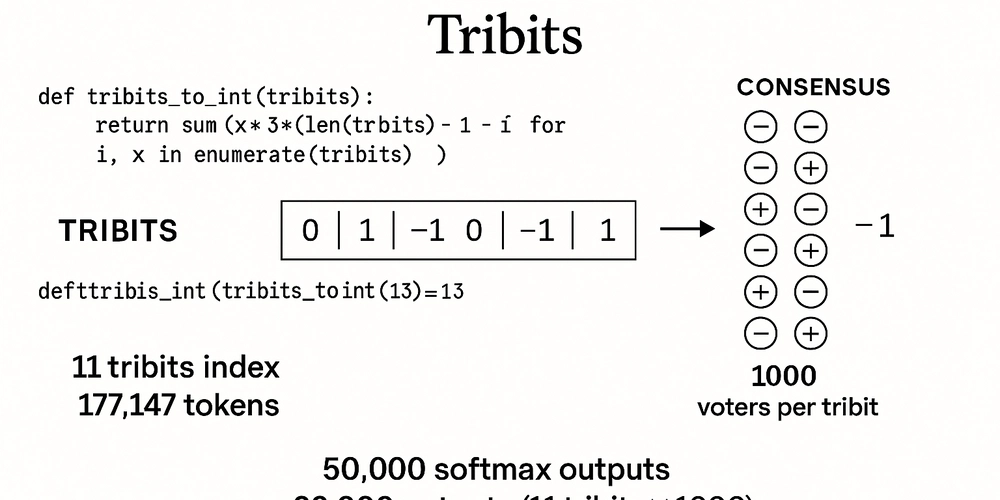
2.2 Tribit Encoding

Rather than working with discrete token IDs directly, we represent tokens using "tribit" encoding—vectors of ternary values (-1, 0, 1). This representation provides:

Smoother embedding space that better captures semantic gradients
More efficient representation than one-hot encoding
Natural handling of uncertainty in token predictions
Enables representation of conceptual "in-betweenness" of tokens

Our training dataset consists of tribit-encoded tokens with the following structure:

class FillInTheBlankDataset(Dataset):
    def __init__(self, csv_path, max_seq_len=64, num_tribits=12, use_tribits=True):
        """
        Dataset for fill-in-the-blank task supporting both tribit and direct token ID encoding.
        """
        self.data = pd.read_csv(csv_path)
        self.data['input_ids'] = self.data['input_ids'].apply(self._safe_eval)
        self.data['target_ids'] = self.data['target_ids'].apply(self._safe_eval)
        self.max_seq_len = max_seq_len
        self.num_tribits = num_tribits
        self.use_tribits = use_tribits

Each target token is represented as a 12-dimensional tribit vector, allowing for nuanced semantic representation beyond discrete token IDs.

2.3 Distance-Based Clustering Loss

We train our model using a specialized distance-based clustering loss with three components:

def distance_based_clustering_loss(outputs, targets, margin=1.5):
    # normalize so everything is on unit sphere
    outputs = F.normalize(outputs.view(batch_size, -1), dim=-1)

    # 1) intra-cluster: minimize distance within same class
    intra_terms = []
    for inds in valid:
        c = outputs[inds].mean(0)
        intra_terms += [torch.sum((outputs[i] - c)**2) for i in inds]
    intra_loss = torch.stack(intra_terms).mean()

    # 2) inter-cluster hinge: maximize distance between different classes
    inter_terms = []
    for i in range(len(keys)):
        for j in range(i+1, len(keys)):
            d = torch.norm(centroids[keys[i]] - centroids[keys[j]], p=2)
            inter_terms.append(torch.clamp(margin - d, min=0.0)**2)
    inter_loss = torch.stack(inter_terms).mean()

    # 3) orthogonality: encourage perpendicular centroids
    ortho_terms = []
    for i in range(len(keys)):
        for j in range(i+1, len(keys)):
            cos_sim = torch.dot(centroids[keys[i]], centroids[keys[j]])
            ortho_terms.append(cos_sim**2)
    ortho_loss = torch.stack(ortho_terms).mean()

    # combine losses
    total = intra_loss + 0.5*inter_loss + 0.2*ortho_loss
    return total, intra_loss, inter_loss, ortho_loss

This approach produces a semantic embedding space with well-separated, coherent clusters representing different linguistic concepts, optimizing for:

Tight clustering of similar tokens (intra-cluster loss)
Good separation between different clusters (inter-cluster loss)
Efficient use of the embedding space dimensions (orthogonality loss)

3. Learning and Representing Centroids

3.1 Centroid Extraction Process

During training, our model naturally forms clusters in embedding space. We extract the centroids of these clusters through a process that:

def extract_centroids(model, dataloader, device):
    """
    Extract cluster centroids from trained model for inference.
    """
    model.eval()
    all_outputs = []
    all_targets = []

    with torch.no_grad():
        for inputs, targets in dataloader:
            inputs, targets = inputs.to(device), targets.to(device)
            raw_outputs = model(inputs)
            outputs = vote_and_collapse(raw_outputs)

            all_outputs.append(outputs)
            all_targets.append(targets)

    # Group by label
    label_groups = {}
    for i in range(all_outputs.shape[0]):
        label_key = label_to_key(all_targets[i])
        if label_key not in label_groups:
            label_groups[label_key] = []
        label_groups[label_key].append(i)

    # Calculate centroids for each label
    centroids = {}
    for label_key, indices in label_groups.items():
        if len(indices) > 0:
            group_outputs = all_outputs[indices]
            centroid = group_outputs.mean(dim=0)
            centroids[label_key] = centroid.cpu()

    return centroids

These centroids represent "prototype" concepts in the embedding space and serve as anchors for inference.

3.2 Centroid Analysis

Our analysis of the extracted centroids revealed several interesting properties:

High dimensional concentration: PCA analysis shows 99.96% of variance is explained by the first principal component, indicating the model has found an extremely efficient encoding.
Columnar organization: Centroids arrange in vertical stripes or columns in PCA projections, suggesting systematic organization of semantic concepts.
Non-random patterns: The regular spacing and organization indicate the model has discovered meaningful structure in the data.

Through visualization (see Figure 1), we observed that rather than forming tight, distinct clusters, the centroids organize along continuous axes in the embedding space, suggesting the model has discovered a continuous semantic space.

4. Probabilistic Token Mapping

4.1 Many-to-Many Relationships

A key insight from our work is the recognition that the relationship between tokens and concepts is many-to-many:

Multiple tokens can map to a single centroid: Semantically similar tokens often cluster together
A single token can map to multiple centroids: Context-dependent token usage is captured naturally

This accurately reflects the contextual nature of language and improves the model's handling of ambiguity.

4.2 Centroid-to-Token Distribution

We create a probabilistic mapping from centroids to tokens by analyzing the training data:

def build_centroid_to_token_mapping(model, dataset, centroids, device):
    """
    Build a mapping from centroids to tokens.
    """
    model.eval()
    centroid_to_tokens = {}

    for inputs, targets in dataloader:
        inputs, targets = inputs.to(device), targets.to(device)

        # Get centroid predictions
        predictions, _ = classify_with_centroids(model, inputs, centroids, device)

        # Update mapping
        for i, prediction in enumerate(predictions):
            target = targets[i]
            token_repr = str(target.tolist())

            if prediction not in centroid_to_tokens:
                centroid_to_tokens[prediction] = {}

            if token_repr not in centroid_to_tokens[prediction]:
                centroid_to_tokens[prediction][token_repr] = 0

            centroid_to_tokens[prediction][token_repr] += 1

    # Calculate probabilities
    for centroid, tokens in centroid_to_tokens.items():
        total = sum(tokens.values())
        centroid_to_tokens[centroid] = {
            'probabilities': {t: count/total for t, count in tokens.items()}
        }

    return centroid_to_tokens

This mapping enables contextually-appropriate token prediction during inference.

4.3 Token Prediction Process

During inference, token prediction follows a two-stage process:

def predict_tokens(self, input_data, k=3, method='top'):
    """
    Predict tokens for an input using probabilistic centroid mapping.
    """
    # Process through model to get embedding
    with torch.no_grad():
        raw_output = self.model(input_data)
        embedding = self.vote_and_collapse(raw_output)[0]

    # Get nearest centroid
    centroid, distance, _ = self.find_nearest_centroid(embedding)

    # Get token distribution for this centroid
    if centroid in self.mapping:
        probs = self.mapping[centroid]['probabilities']

        # Return top-k tokens
        top_tokens = sorted(probs.items(), key=lambda x: x[1], reverse=True)[:k]
        return top_tokens, distance, centroid

This approach naturally handles ambiguity and provides a measure of prediction confidence through centroid distances.

5. Experimental Results

5.1 Consistency Analysis

Our consistency analysis reveals interesting patterns in how inputs with the same ground truth label map to centroids:

Testing consistency for label: (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0)
  Sample 1: Pred=(0, 0, 0, 0, 0, 1, 1, 0, -1, 0, 1, 0), Dist=0.0000, Margin=0.0009
  Sample 2: Pred=(0, 0, 1, -1, 1, 1, -1, 0, 1, -1, -1, -1), Dist=0.0011, Margin=0.0008
  ...
  Consistency score: 20.00%
  Avg internal distance: 0.8682
  Avg distance to centroid: 0.0012

Key observations:

Low consistency scores (10-30%) indicate inputs with the same label map to different centroids
Very small distances to centroids (0.0000-0.0103) show precise mapping to the centroid space
High internal distances (0.7498-0.9545) indicate widespread distribution of semantically related inputs

These results demonstrate the model has discovered semantic relationships beyond simple label matching.

5.2 Token Prediction Analysis

Our token mapping analysis showed several interesting patterns:

Ambiguous centroids: Some centroids map to many different tokens, suggesting they capture higher-level semantic categories
Versatile tokens: Some tokens appear in many centroids, indicating context-dependent usage
Precise mapping: Despite the many-to-many relationship, the model achieves high precision in mapping inputs to semantically appropriate centroids

Analyzing the token prediction process reveals that top predicted tokens for each centroid typically share semantic or functional relationships, even when they differ in surface form.

5.3 Semantic Space Visualization

Visualizations of the embedding space reveal clear structural organization:

Diagonal patterns in PCA projections showing conceptual axes
Repeating structures suggesting hierarchical organization of semantic concepts
Regular spacing indicating systematic organization of the embedding space

These patterns support our hypothesis that the model has discovered meaningful linguistic structure beyond simple memorization of token patterns.

6. Discussion and Future Work

6.1 Advantages of Centroid-Based Approach

The centroid-based approach offers several advantages:

Interpretability: The model's decisions can be traced through embedding space to specific centroids
Robustness: Semantic ambiguity is handled through probabilistic mapping from centroids to tokens
Flexibility: New tokens can be added to existing centroids without retraining the entire model
Efficiency: Centroids provide an efficient summary of the semantic space

6.2 Limitations and Challenges

Our approach also faces several limitations:

Training complexity: The distance-based clustering loss requires careful tuning
Centroid coverage: Not all possible token patterns may be represented in the centroid space
Computational efficiency: Comparing against all centroids during inference can be expensive
Evaluation metrics: Traditional accuracy metrics don't fully capture the semantic mapping quality

6.3 Future Directions

Promising directions for future work include:

Hierarchical centroids: Organizing centroids in a hierarchical structure for more efficient lookup
Dynamic centroid adaptation: Allowing centroids to evolve during fine-tuning or inference
Context-weighted prediction: Using context to weight the probability of different tokens for each centroid
Cross-lingual applications: Extending the approach to map between different languages using shared centroid space
Larger vocabulary: Scaling to much larger vocabulary sizes while maintaining semantic coherence

7. Conclusion

The ElasticFourierTransformer with probabilistic centroid mapping represents a novel approach to language modeling that captures the rich, contextual nature of language. By separating the mapping from context to embedding space from the mapping from embeddings to tokens, we enable more interpretable, robust prediction.

Our analysis demonstrates that the model discovers meaningful linguistic structure beyond its explicit training objective, suggesting promising directions for more semantically grounded NLP systems. The many-to-many relationship between tokens and centroids provides a natural way to model semantic ambiguity, while the precise mapping to centroids ensures high-quality predictions.

This approach offers a new perspective on language modeling that prioritizes semantic understanding over simple pattern matching, potentially leading to more robust, interpretable, and flexible language technologies.

Acknowledgments

[To be added]

References

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.
Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., ... & Amodei, D. (2020). Language models are few-shot learners. arXiv preprint arXiv:2005.14165.
Conneau, A., Khandelwal, K., Goyal, N., Chaudhary, V., Wenzek, G., Guzmán, F., ... & Stoyanov, V. (2020). Unsupervised cross-lingual representation learning at scale. arXiv preprint arXiv:1911.02116.
Clark, K., Luong, M. T., Le, Q. V., & Manning, C. D. (2020). Electra: Pre-training text encoders as discriminators rather than generators. arXiv preprint arXiv:2003.10555.
Hewitt, J., & Manning, C. D. (2019). A structural probe for finding syntax in word representations. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers) (pp. 4129-4138).
Mathieu, E., Le Lan, C., Maddison, C. J., Tomioka, R., & Teh, Y. W. (2019). Continuous hierarchical representations with poincaré variational auto-encoders. Advances in neural information processing systems, 32.
Lin, T., Wang, Y., Liu, X., & Qiu, X. (2021). A survey of transformers. arXiv preprint arXiv:2106.04554.