2551. Put Marbles in Bags

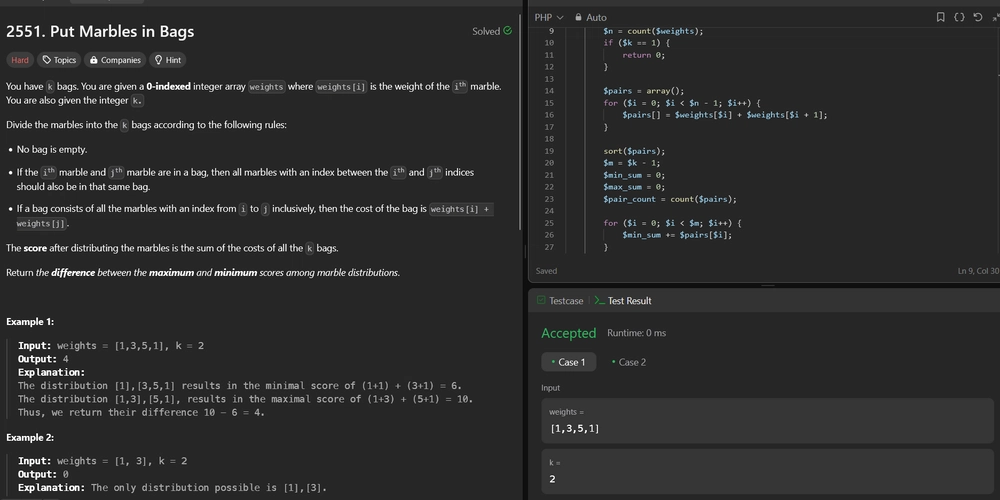
2551. Put Marbles in Bags Difficulty: Hard Topics: Array, Greedy, Sorting, Heap (Priority Queue) You have k bags. You are given a 0-indexed integer array weights where weights[i] is the weight of the ith marble. You are also given the integer k. Divide the marbles into the k bags according to the following rules: No bag is empty. If the ith marble and jth marble are in a bag, then all marbles with an index between the ith and jth indices should also be in that same bag. If a bag consists of all the marbles with an index from i to j inclusively, then the cost of the bag is weights[i] + weights[j]. The score after distributing the marbles is the sum of the costs of all the k bags. Return the difference between the maximum and minimum scores among marble distributions. Example 1: Input: weights = [1,3,5,1], k = 2 Output: 4 Explanation: The distribution [1],[3,5,1] results in the minimal score of (1+1) + (3+1) = 6. The distribution [1,3],[5,1], results in the maximal score of (1+3) + (5+1) = 10. Thus, we return their difference 10 - 6 = 4. Example 2: Input: weights = [1, 3], k = 2 Output: 0 Explanation: The only distribution possible is [1],[3]. Since both the maximal and minimal score are the same, we return 0. Constraints: 1 Explanation: Handling Edge Case: If k is 1, the only possible distribution is the entire array itself, resulting in a fixed score, so the difference is 0. Calculating Adjacent Pairs: For each adjacent pair of elements in the array, compute their sum. These sums represent the possible split points between subarrays. Sorting Pairs: Sort the array of adjacent sums to efficiently determine the largest and smallest sums. Summing Extremes: Calculate the sum of the smallest k-1 and largest k-1 elements from the sorted array. The difference between these sums gives the desired result. This approach efficiently computes the required difference using sorting and summation, ensuring optimal performance even for large input sizes. Contact Links If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks

Mar 31, 2025 - 02:40

Difficulty: Hard

Topics: Array, Greedy, Sorting, Heap (Priority Queue)

You have k bags. You are given a 0-indexed integer array weights where weights[i] is the weight of the i^th marble. You are also given the integer k.

Divide the marbles into the k bags according to the following rules:

No bag is empty.
If the i^th marble and j^th marble are in a bag, then all marbles with an index between the ith and jth indices should also be in that same bag.
If a bag consists of all the marbles with an index from i to j inclusively, then the cost of the bag is weights[i] + weights[j].

The score after distributing the marbles is the sum of the costs of all the k bags.

Return the difference between the maximum and minimum scores among marble distributions.

Example 1:

Input: weights = [1,3,5,1], k = 2
Output: 4
Explanation:
- The distribution [1],[3,5,1] results in the minimal score of (1+1) + (3+1) = 6.
- The distribution [1,3],[5,1], results in the maximal score of (1+3) + (5+1) = 10.
- Thus, we return their difference 10 - 6 = 4.

Example 2:

Input: weights = [1, 3], k = 2
Output: 0
Explanation: The only distribution possible is [1],[3].
- Since both the maximal and minimal score are the same, we return 0.

Constraints:

1 <= k <= weights.length <= 10⁵
1 <= weights[i] <= 10⁹

Hint:

Each bag will contain a subarray, and only the endpoints of these subarrays matter.
Each subarray only contributes two numbers to the sum. Use this property to choose the subarrays optimally.
Try to use a priority queue.

Solution:

We need to determine the difference between the maximum and minimum possible scores when distributing marbles into k bags. Each bag must contain contiguous subarrays of marbles, and the score for each bag is the sum of the first and last marble's weight in that bag.

Approach

Understanding the Problem Constraints: Each bag must be a contiguous subarray. The score for each bag is the sum of the first and last elements of the subarray. The goal is to find the difference between the maximum and minimum scores possible with k bags.
Key Insight: The score for each bag can be determined by the sum of the first and last elements of each subarray. When splitting the array into k contiguous subarrays, the score is influenced by the sum of adjacent elements at the split points.
Formulating the Solution:
- Calculate the sum of adjacent elements for all possible split points.
- Sort these sums.
- The maximum score is obtained by taking the largest k-1 sums.
- The minimum score is obtained by taking the smallest k-1 sums.
- The difference between these sums gives the result.

Let's implement this solution in PHP: 2551. Put Marbles in Bags


/**
 * @param Integer[] $weights
 * @param Integer $k
 * @return Integer
 */
function putMarbles($weights, $k) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example test cases
$weights1 = [1, 3, 5, 1];
$k1 = 2;
echo putMarbles($weights1, $k1) . "\n"; // Output: 4

$weights2 = [1, 3];
$k2 = 2;
echo putMarbles($weights2, $k2) . "\n"; // Output: 0
?>

Explanation:

Handling Edge Case: If k is 1, the only possible distribution is the entire array itself, resulting in a fixed score, so the difference is 0.
Calculating Adjacent Pairs: For each adjacent pair of elements in the array, compute their sum. These sums represent the possible split points between subarrays.
Sorting Pairs: Sort the array of adjacent sums to efficiently determine the largest and smallest sums.
Summing Extremes: Calculate the sum of the smallest k-1 and largest k-1 elements from the sorted array. The difference between these sums gives the desired result.

This approach efficiently computes the required difference using sorting and summation, ensuring optimal performance even for large input sizes.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks