Understanding SVD's Intuition (Singular Value Decomposition)
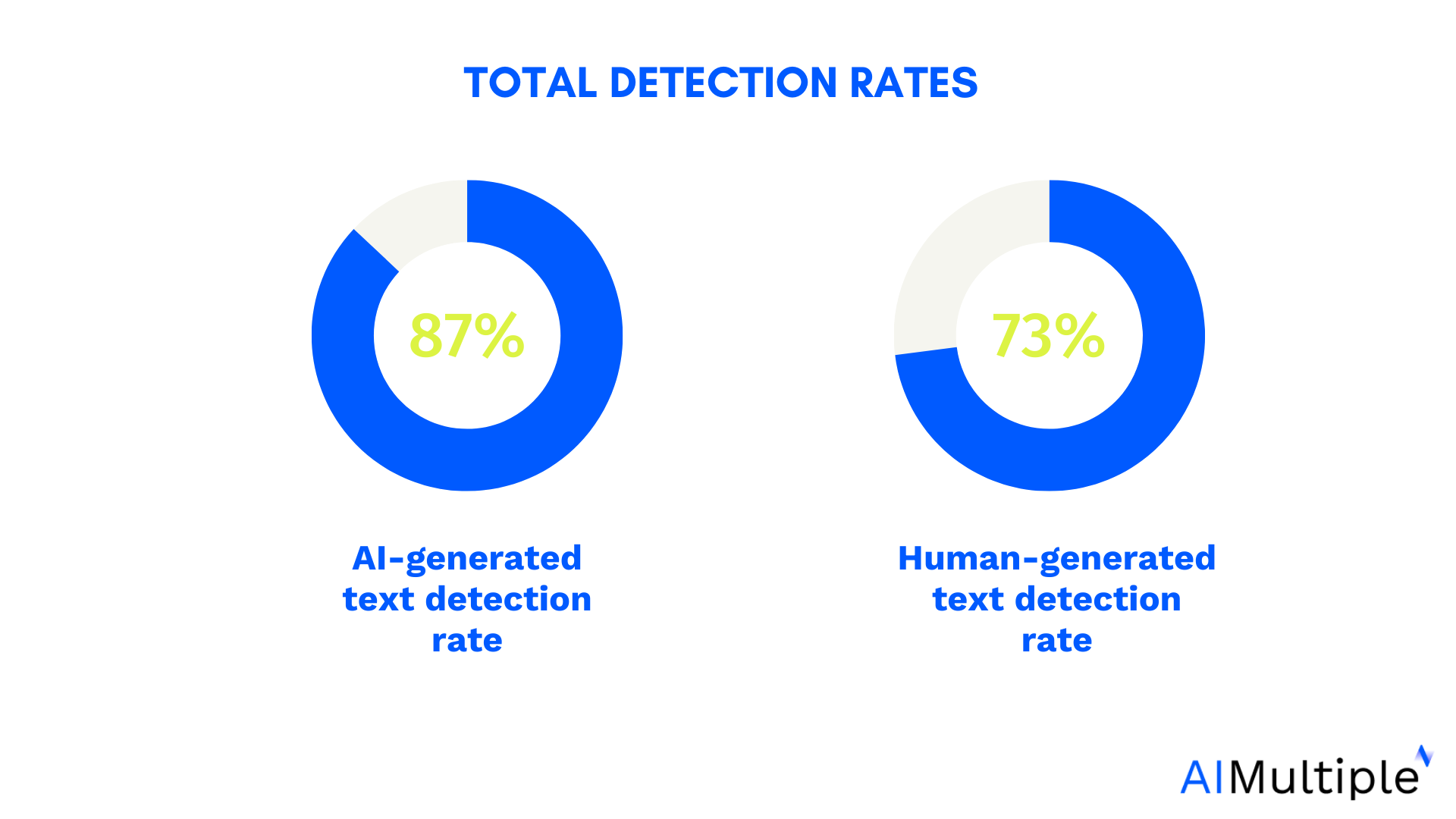
What is SVD Singular Value Decomposition (SVD) is a fundamental matrix factorisation technique in linear algebra that decomposes a matrix into three simpler component matrices. It's incredibly versatile and powerful, serving as the backbone for numerous applications across various fields. Why Was SVD Developed? SVD was developed to solve the problem of finding the best approximation of a matrix by a lower-rank matrix. Mathematicians needed a way to: Factorise the original matrix into three smaller matrices that capture hidden relationship , It will find latent features that explain the patterns in a given matrix. Understand the fundamental structure of linear transformations. Analyse the underlying properties of matrices regardless of their dimensions. The core purpose was to find a way to decompose any matrix into simpler, more manageable components that reveal its essential properties - specifically its rank, range (column space), and null space. What does it mean to find the best approximation of a matrix by a lower-rank matrix? When we have a large, complex matrix A with rank r, we often want to simplify it to save computational resources while preserving as much of the original information as possible. Finding the "best approximation" means: Creating a new matrix  with lower rank k (where k < r) Ensuring this approximation minimises the error (typically measured as the Frobenius norm ||A - Â||) Capturing the most important patterns/structures in the original data This is valuable because lower-rank matrices: Require less storage space Allow faster computations Often filter out noise while preserving signal What is a Latent Feature? A latent feature is: A property or concept that isn't explicitly observed in the data, but is inferred from patterns across the matrix. In simple terms: It's a hidden factor that explains why people behave the way they do. You don’t know what it is, but you see its effects. Analogy: Music Taste Imagine a user-song matrix: rows = users, columns = songs, entries = ratings. You don’t label features like "likes punk rock" or "prefers instrumental", but... If two users rate the same songs highly, And those songs share some vibe, Then you can infer there's some latent preference shared. That hidden dimension — like “preference for energetic music” — is a latent feature. Definition Given any real matrix A ∈ ℝm×n, SVD says: Where: Component Shape Role U ℝm×k Orthonormal matrix — maps original rows into a k-dimensional latent space. Each row is a **latent [[Vectors\ Σ ℝk×k Diagonal matrix with non-negative real numbers called singular values, sorted from largest to smallest. These represent the importance (energy) of each dimension in the latent space. Vᵀ ℝk×n Orthonormal matrix — maps original columns into the same k-dimensional latent space. Each column is a latent vector for a column of A. The value k = rank(A) in exact decomposition, or you can choose a smaller k for approximation (low-rank SVD).

What is SVD
Singular Value Decomposition (SVD) is a fundamental matrix factorisation technique in linear algebra that decomposes a matrix into three simpler component matrices. It's incredibly versatile and powerful, serving as the backbone for numerous applications across various fields.
Why Was SVD Developed?
SVD was developed to solve the problem of finding the best approximation of a matrix by a lower-rank matrix. Mathematicians needed a way to:
- Factorise the original matrix into three smaller matrices that capture hidden relationship , It will find latent features that explain the patterns in a given matrix.
- Understand the fundamental structure of linear transformations.
- Analyse the underlying properties of matrices regardless of their dimensions.
The core purpose was to find a way to decompose any matrix into simpler, more manageable components that reveal its essential properties - specifically its rank, range (column space), and null space.
What does it mean to find the best approximation of a matrix by a lower-rank matrix?
When we have a large, complex matrix A with rank r, we often want to simplify it to save computational resources while preserving as much of the original information as possible.
Finding the "best approximation" means:
- Creating a new matrix  with lower rank k (where k < r)
- Ensuring this approximation minimises the error (typically measured as the Frobenius norm ||A - Â||)
- Capturing the most important patterns/structures in the original data
This is valuable because lower-rank matrices:
- Require less storage space
- Allow faster computations
- Often filter out noise while preserving signal
What is a Latent Feature?
A latent feature is:
A property or concept that isn't explicitly observed in the data, but is inferred from patterns across the matrix.
In simple terms:
- It's a hidden factor that explains why people behave the way they do.
- You don’t know what it is, but you see its effects.
Analogy: Music Taste
Imagine a user-song matrix: rows = users, columns = songs, entries = ratings.
You don’t label features like "likes punk rock" or "prefers instrumental", but...
- If two users rate the same songs highly,
- And those songs share some vibe,
Then you can infer there's some latent preference shared.
That hidden dimension — like “preference for energetic music” — is a latent feature.
Definition
Given any real matrix A ∈ ℝm×n, SVD says:
Where:
| Component | Shape | Role |
|---|---|---|
| U | ℝm×k | Orthonormal matrix — maps original rows into a k-dimensional latent space. Each row is a **latent [[Vectors\ |
| Σ | ℝk×k | Diagonal matrix with non-negative real numbers called singular values, sorted from largest to smallest. These represent the importance (energy) of each dimension in the latent space. |
| Vᵀ | ℝk×n | Orthonormal matrix — maps original columns into the same k-dimensional latent space. Each column is a latent vector for a column of A. |
The value k = rank(A) in exact decomposition, or you can choose a smaller k for approximation (low-rank SVD).





































































































































































![[The AI Show Episode 145]: OpenAI Releases o3 and o4-mini, AI Is Causing “Quiet Layoffs,” Executive Order on Youth AI Education & GPT-4o’s Controversial Update](https://www.marketingaiinstitute.com/hubfs/ep%20145%20cover.png)





















































































































![Ditching a Microsoft Job to Enter Startup Purgatory with Lonewolf Engineer Sam Crombie [Podcast #171]](https://cdn.hashnode.com/res/hashnode/image/upload/v1746753508177/0cd57f66-fdb0-4972-b285-1443a7db39fc.png?#)


































































































































_Piotr_Adamowicz_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)




















































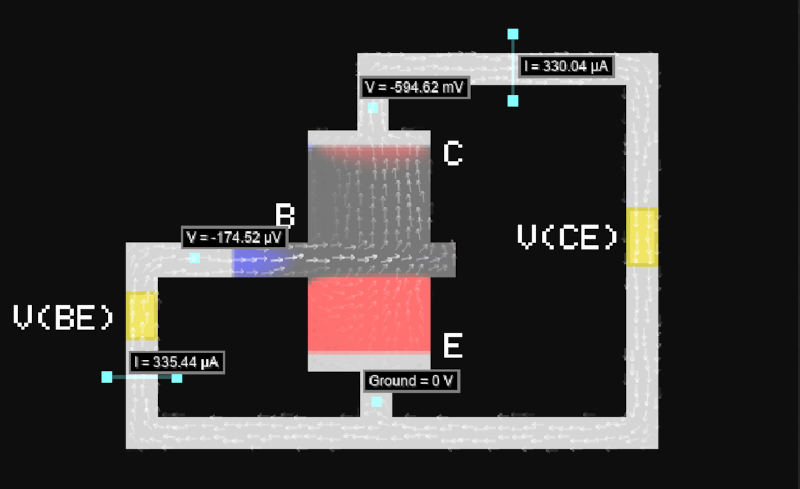


























-xl-xl-xl.jpg)












![Walmart’s $30 Google TV streamer is now in stores and it supports USB-C hubs [Video]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2025/05/onn-4k-plus-store-reddit.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)












![Apple to Launch AI-Powered Battery Saver Mode in iOS 19 [Report]](https://www.iclarified.com/images/news/97309/97309/97309-1280.jpg)

![Apple Officially Releases macOS Sequoia 15.5 [Download]](https://www.iclarified.com/images/news/97308/97308/97308-640.jpg)