2145. Count the Hidden Sequences

2145. Count the Hidden Sequences Difficulty: Medium Topics: Array, Prefix Sum You are given a 0-indexed array of n integers differences, which describes the differences between each pair of consecutive integers of a hidden sequence of length (n + 1). More formally, call the hidden sequence hidden, then we have that differences[i] = hidden[i + 1] - hidden[i]. You are further given two integers lower and upper that describe the inclusive range of values [lower, upper] that the hidden sequence can contain. For example, given differences = [1, -3, 4], lower = 1, upper = 6, the hidden sequence is a sequence of length 4 whose elements are in between 1 and 6 (inclusive). [3, 4, 1, 5] and [4, 5, 2, 6] are possible hidden sequences. [5, 6, 3, 7] is not possible since it contains an element greater than 6. [1, 2, 3, 4] is not possible since the differences are not correct. Return the number of possible hidden sequences there are. If there are no possible sequences, return 0. Example 1: Input: differences = [1,-3,4], lower = 1, upper = 6 Output: 2 Explanation: The possible hidden sequences are: [3, 4, 1, 5] [4, 5, 2, 6] Thus, we return 2. Example 2: Input: differences = [3,-4,5,1,-2], lower = -4, upper = 5 Output: 4 Explanation: The possible hidden sequences are: [-3, 0, -4, 1, 2, 0] [-2, 1, -3, 2, 3, 1] [-1, 2, -2, 3, 4, 2] [0, 3, -1, 4, 5, 3] Thus, we return 4. Example 3: Input: differences = [4,-7,2], lower = 3, upper = 6 Output: 0 Explanation: There are no possible hidden sequences. Thus, we return 0. Constraints: n == differences.length 1

Apr 21, 2025 - 21:12

Difficulty: Medium

Topics: Array, Prefix Sum

You are given a 0-indexed array of n integers differences, which describes the differences between each pair of consecutive integers of a hidden sequence of length (n + 1). More formally, call the hidden sequence hidden, then we have that differences[i] = hidden[i + 1] - hidden[i].

You are further given two integers lower and upper that describe the inclusive range of values [lower, upper] that the hidden sequence can contain.

For example, given differences = [1, -3, 4], lower = 1, upper = 6, the hidden sequence is a sequence of length 4 whose elements are in between 1 and 6 (inclusive).
- [3, 4, 1, 5] and [4, 5, 2, 6] are possible hidden sequences.
- [5, 6, 3, 7] is not possible since it contains an element greater than 6.
- [1, 2, 3, 4] is not possible since the differences are not correct.

Return the number of possible hidden sequences there are. If there are no possible sequences, return 0.

Example 1:

Input: differences = [1,-3,4], lower = 1, upper = 6
Output: 2
Explanation: The possible hidden sequences are:
- [3, 4, 1, 5]
- [4, 5, 2, 6]
- Thus, we return 2.

Example 2:

Input: differences = [3,-4,5,1,-2], lower = -4, upper = 5
Output: 4
Explanation: The possible hidden sequences are:
- [-3, 0, -4, 1, 2, 0]
- [-2, 1, -3, 2, 3, 1]
- [-1, 2, -2, 3, 4, 2]
- [0, 3, -1, 4, 5, 3]
- Thus, we return 4.

Example 3:

Input: differences = [4,-7,2], lower = 3, upper = 6
Output: 0
Explanation: There are no possible hidden sequences. Thus, we return 0.

Constraints:

n == differences.length
1 <= n <= 10⁵
-10⁵ <= differences[i] <= 10⁵
-10⁵ <= lower <= upper <= 10⁵

Hint:

Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array.
We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this.
We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper.
Answer is (upper - lower + 1) - (range of sequence)

Solution:

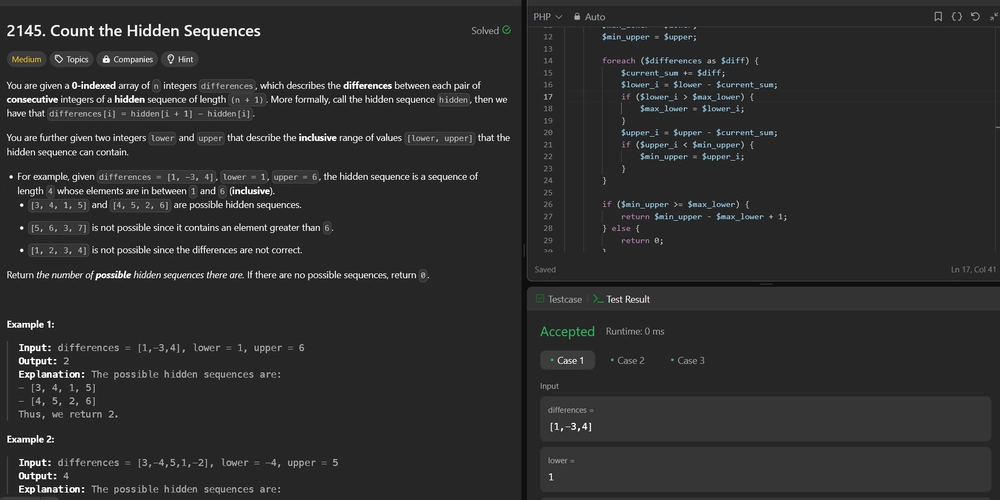
We need to determine the number of valid hidden sequences that can be formed given a list of differences between consecutive elements and a range [lower, upper] within which all elements of the hidden sequence must lie.

Approach

Prefix Sum Calculation: The hidden sequence can be derived using the given differences. The key observation is that the hidden sequence can be represented using prefix sums. If we start with an initial value x, each subsequent element can be determined by adding the corresponding prefix sum of the differences to x.
Determine Bounds for x: For the hidden sequence to be valid, every element must lie within [lower, upper]. This translates to finding the range of possible values for x such that all elements derived from x fall within the given bounds.
Track Maximum and Minimum Constraints: Compute the maximum lower bound and minimum upper bound for x by iterating through the prefix sums. The valid range for x is the intersection of all possible intervals derived from each prefix sum.
Count Valid Values: The number of valid values for x is determined by the overlap of the computed maximum lower bound and minimum upper bound. If there is no overlap, the result is zero; otherwise, the count is the length of the overlapping interval.

Let's implement this solution in PHP: 2145. Count the Hidden Sequences


/**
 * @param Integer[] $differences
 * @param Integer $lower
 * @param Integer $upper
 * @return Integer
 */
function numberOfArrays($differences, $lower, $upper) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/ Example 1
echo numberOfArrays([1, -3, 4], 1, 6) . "\n"; // Output: 2

// Example 2
echo numberOfArrays([3, -4, 5, 1, -2], -4, 5) . "\n"; // Output: 4

// Example 3
echo numberOfArrays([4, -7, 2], 3, 6) . "\n"; // Output: 0
?>

Explanation:

Prefix Sum Calculation: We start with an initial prefix sum of 0 and iteratively compute the prefix sums for the given differences. This helps in determining the relative values of the hidden sequence elements.
Tracking Bounds: For each prefix sum, we compute the lower and upper bounds for the initial value x such that all elements derived from x stay within [lower, upper]. We maintain the maximum of all lower bounds and the minimum of all upper bounds.
Valid Range Check: After processing all differences, we check if the computed maximum lower bound is less than or equal to the minimum upper bound. If it is, the number of valid initial values x is the length of the interval plus one (to include both endpoints). If not, there are no valid sequences.

This approach efficiently computes the valid range for x in linear time, making it suitable for large input sizes as specified in the problem constraints.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks