1007. Minimum Domino Rotations For Equal Row

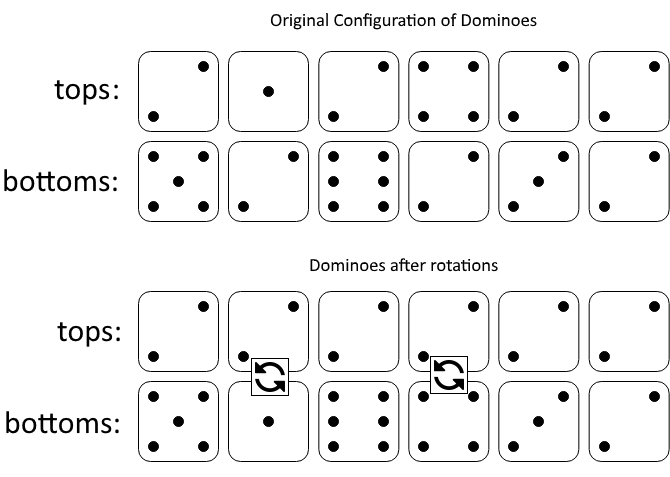
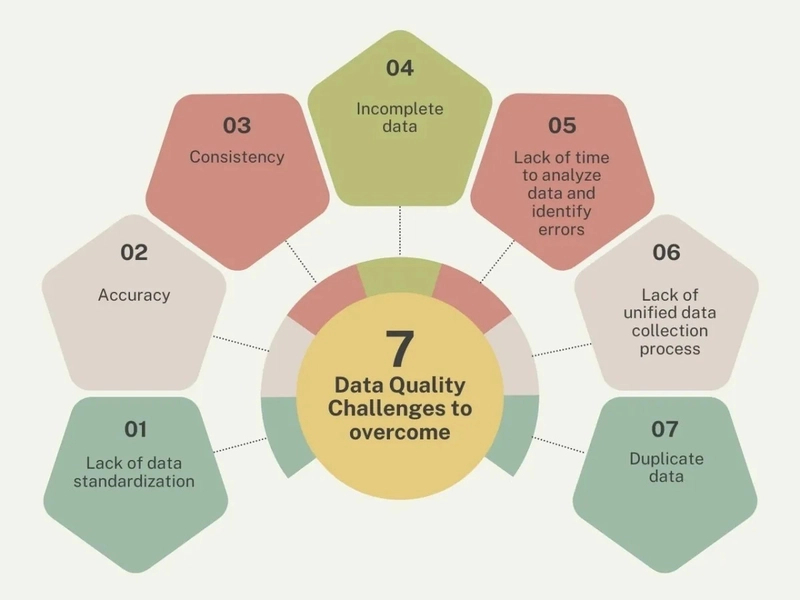
1007. Minimum Domino Rotations For Equal Row Difficulty: Medium Topics: Array, Greedy In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.) We may rotate the ith domino, so that tops[i] and bottoms[i] swap values. Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same. If it cannot be done, return -1. Example 1: Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2] Output: 2 Explanation: The first figure represents the dominoes as given by tops and bottoms: before we do any rotations. If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure. Example 2: Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4] Output: -1 Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal. Constraints: 2

May 3, 2025 - 17:11

Difficulty: Medium

Topics: Array, Greedy

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the i^th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i^th domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Example 1:

Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation: The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
- If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

2 <= tops.length <= 2 * 10⁴
bottoms.length == tops.length
1 <= tops[i], bottoms[i] <= 6

Solution:

We need to determine the minimum number of rotations required to make all values in either the top row or the bottom row of a set of dominoes the same. If it is not possible, we should return -1.

Approach

Identify Candidates: The target value (which all dominoes must be rotated to) must be present in either the top or bottom of the first domino. This is because if the target value is not in the first domino, it is impossible to make all values in either row match that target.
Check Validity: For each candidate value from the first domino, check if every domino can contribute this value to either the top or bottom row. If any domino cannot contribute this value, the candidate is invalid.
Calculate Rotations: For each valid candidate, calculate the number of rotations needed to make all top values the same and the number of rotations needed to make all bottom values the same. The minimum of these two values is the result for that candidate.
Determine Result: The result is the minimum value among all valid candidates. If no valid candidates exist, return -1.

Let's implement this solution in PHP: 1007. Minimum Domino Rotations For Equal Row


/**
 * @param Integer[] $tops
 * @param Integer[] $bottoms
 * @return Integer
 */
function minDominoRotations($tops, $bottoms) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example 1:
$tops1 = [2,1,2,4,2,2];
$bottoms1 = [5,2,6,2,3,2];
echo minDominoRotations($tops1, $bottoms1) . "\n"; // Output: 2

// Example 2:
$tops2 = [3,5,1,2,3];
$bottoms2 = [3,6,3,3,4];
echo minDominoRotations($tops2, $bottoms2) . "\n"; // Output: -1
?>

Explanation:

Identify Candidates: The candidates are derived from the first domino's top and bottom values.
Check Validity: For each candidate, iterate through all dominoes to check if the candidate value is present in either the top or bottom of each domino.
Calculate Rotations: For each valid candidate, count the number of rotations needed to align all tops or all bottoms with the candidate value. The count is determined by how many dominoes need to be flipped to achieve the target value in the desired row.
Determine Result: The minimum rotations across all valid candidates is the solution. If no valid candidates are found, return -1.

This approach efficiently narrows down the possible target values and checks each one in linear time, resulting in an overall time complexity of O(n), where n is the number of dominoes.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks