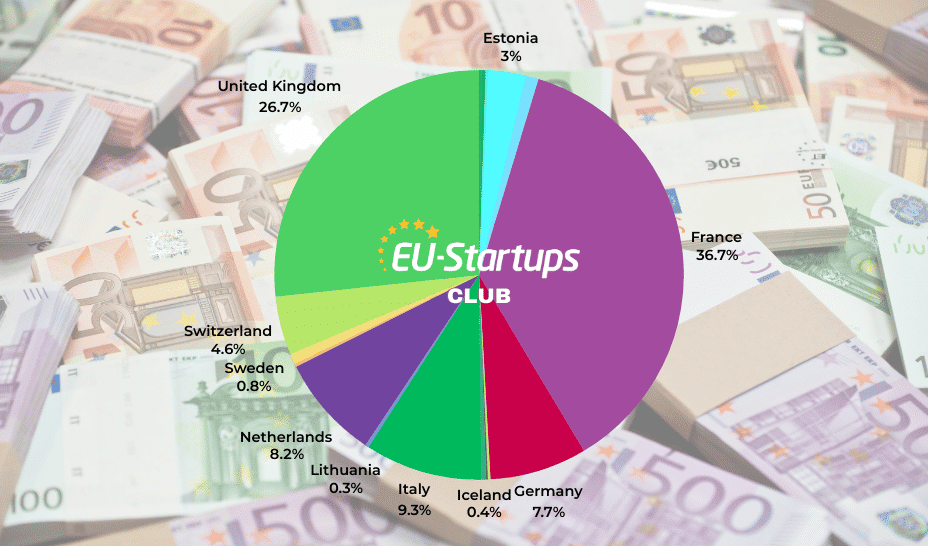
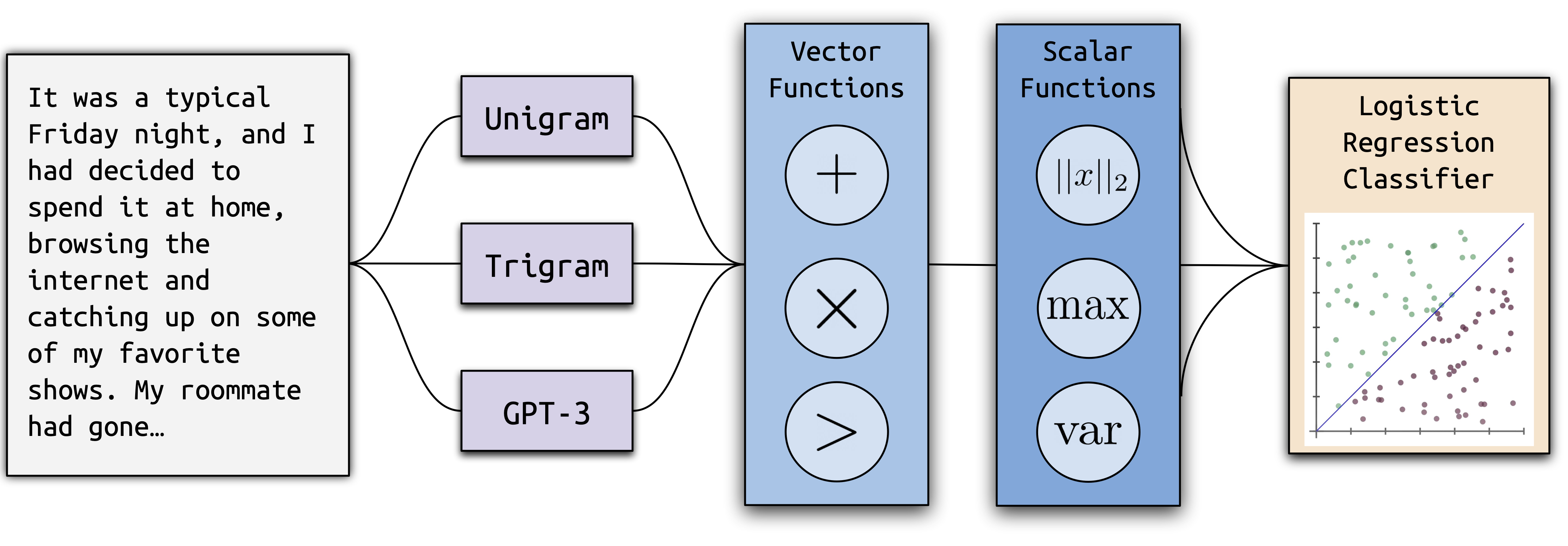
Ways to normalize/standardize an array

In Data Science, it is common place to normalize array data, such that the minimum and maximum values are 0 and 1, respectively. Similarly, array data can be scaled by the spread (standard deviation) and mean of the data, called standardization of data. const x = [0.45, 0.45, 0.46, 0.56, 0.34, 0.05, 0.34, 0.56, 0.46, 0.44]; var output0 = normalization(x); console.log("output0: ", output0); var output1 = baseline_shift_maxScale(x); console.log("output1: ", output1); var output2 = standardization(x); console.log("output2: ", output2); function normalization(x) { return x.map((v,i) => { return (v-x.sort().at(0))/(x.sort().at(-1) - x.sort().at(0)); }); } function standardization(x) { var mu = x.reduce((a,c) => a+c, 0)/x.length; var sum_difference = x.map((v,i) => { return Math.pow(v-mu,2); }).reduce((a,c) => a+c, 0)/x.length; var sigma = Math.sqrt(sum_difference); return x.map((v,i) => { return (v-mu)/sigma; }); } function baseline_shift_maxScale(x) { var x_baseline_shift = x.map((v,i) => { return v-x.sort().at(0); }); return x_baseline_shift.map((v,i) => { return v/x_baseline_shift.sort().at(-1); }); } Output For the normalization equation, the results are as follows. Notice that sometimes there will not be a 0 value, but it will be close to zero. "output0: " Array [0.7843137254901961, 0.5686274509803922, 0.5686274509803922, 0.7647058823529412, 0.7843137254901961, 0.7843137254901961, 0.803921568627451, 0.803921568627451, 1, 1] For the baseline shift normalization, there will aways be a 0 and 1 value. "output1: " Array [0, 0.5686274509803922, 0.5686274509803922, 0.7647058823529412, 0.7843137254901961, 0.7843137254901961, 0.803921568627451, 0.803921568627451, 1, 1] For standardization, the range will be centered about zero. "output2: " Array [-2.5952424698247905, -0.5104216491899166, -0.5104216491899166, 0.20848208206348795, 0.2803724551888285, 0.2803724551888285, 0.352262828314169, 0.352262828314169, 1.071166559567574, 1.071166559567574] Good Luck and Happy Practicing!

Mar 16, 2025 - 19:05

In Data Science, it is common place to normalize array data, such that the minimum and maximum values are 0 and 1, respectively.

Similarly, array data can be scaled by the spread (standard deviation) and mean of the data, called standardization of data.

const x = [0.45, 0.45, 0.46, 0.56, 0.34, 0.05, 0.34, 0.56, 0.46, 0.44];

var output0 = normalization(x);
console.log("output0: ", output0);

var output1 = baseline_shift_maxScale(x);
console.log("output1: ", output1);

var output2 = standardization(x);
console.log("output2: ", output2);



function normalization(x) {
  return x.map((v,i) => { return (v-x.sort().at(0))/(x.sort().at(-1) - x.sort().at(0)); });
}


function standardization(x) {
  var mu = x.reduce((a,c) => a+c, 0)/x.length;
  var sum_difference = x.map((v,i) => { return Math.pow(v-mu,2); }).reduce((a,c) => a+c, 0)/x.length;
  var sigma = Math.sqrt(sum_difference);

  return x.map((v,i) => { return (v-mu)/sigma; });
}


function baseline_shift_maxScale(x) {
  var x_baseline_shift = x.map((v,i) => { return v-x.sort().at(0); });
  return x_baseline_shift.map((v,i) => { return v/x_baseline_shift.sort().at(-1); });
}

Output

For the normalization equation, the results are as follows. Notice that sometimes there will not be a 0 value, but it will be close to zero.
"output0: " Array [0.7843137254901961, 0.5686274509803922, 0.5686274509803922, 0.7647058823529412, 0.7843137254901961, 0.7843137254901961, 0.803921568627451, 0.803921568627451, 1, 1]

For the baseline shift normalization, there will aways be a 0 and 1 value.
"output1: " Array [0, 0.5686274509803922, 0.5686274509803922, 0.7647058823529412, 0.7843137254901961, 0.7843137254901961, 0.803921568627451, 0.803921568627451, 1, 1]

For standardization, the range will be centered about zero.
"output2: " Array [-2.5952424698247905, -0.5104216491899166, -0.5104216491899166, 0.20848208206348795, 0.2803724551888285, 0.2803724551888285, 0.352262828314169, 0.352262828314169, 1.071166559567574, 1.071166559567574]

Good Luck and Happy Practicing!