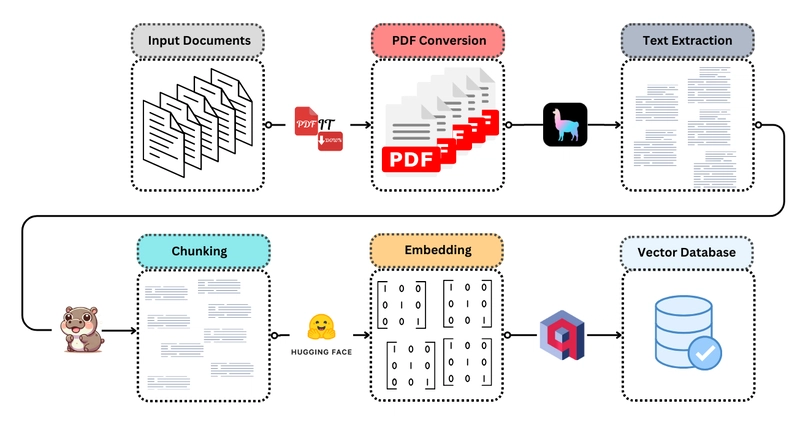
Software Testing: Theory and Practice (Part 5) - How to Select Test Cases

Key Takeaways This Time There are several approaches to sampling a specification. In this article we introduce two: A boundary-value approach (On–Off Point method) A property-based testing approach Methods for Sampling a Specification In previous installments we explained that confirming “the implementation satisfies the specification” often requires an enormous—frequently infinite—number of test cases. In practice, rather than checking every possible case, we sample the specification, verify behaviour for only a very small subset, and infer behaviour for the rest. Ways to sample a specification are also called test design techniques, and many techniques have been proposed. This article introduces the boundary-value approach and the property-based testing approach1. Boundary-Value Approach (On–Off Point Method) The boundary-value approach, Boundary-Value Analysis (BVA), selects inputs called boundary values as samples of the specification. A boundary value is an input at which the branch executed by the hypothetical implementation changes when it contains conditional statements such as if or switch. Experience tells us that many defects lurk at boundary values. A typical example is confusing x < y with x ≤ y or vice versa. In such cases the outputs of x < y and x ≤ y differ only when x = y (here “=” means equality, not assignment). The input satisfying x = y is exactly the boundary value. Certain assumptions must hold for the boundary-value approach to work as intended. 1. The hypothetical implementation has a top-level conditional branch and is followed only by simple processing that contains no loops or recursion. For example, the function isAdult in Code 1, which takes a non-negative age and returns true if the age is an adult and false otherwise, is a typical case. Code 1. Hypothetical implementation of isAdult, which determines adulthood function isAdult(age: number): boolean { // NOTE: Written verbosely for clarity instead of “return 20 0 instead of x > 1 Closure defect – e.g. writing x ≤ 0 instead of x < 0 Missing boundary – forgetting to branch where a boundary should exist Extraneous boundary – introducing a branch where none is needed To uncover all four types, we select, for every boundary in every conditional branch of the implementation, an input exactly on the boundary, and the nearest input on either side of that boundary. Put differently, we “pick the two closest values that lead to different processing”. This is Boundary-Value Analysis (the On–Off Point method). Applied to the earlier isAdult function, boundary-value analysis means testing the cases where age is 19 and 20. Property-Based Testing We explained that boundary-value testing requires assumptions about the component’s implementation. Components that violate those assumptions cannot be tested this way. For such components I recommend adopting Property-Based Testing (PBT). We have mentioned PBT in prior installments, but here is a refresher. In traditional Example-Based Testing (EBT), humans choose the inputs. In contrast, PBT automatically generates inputs. The human supplies a relationship that must hold between input and output, and the output is checked against it. This relationship is typically a post-condition3. For the FizzBuzz function, for example, we might give the following post-conditions: If the input is divisible by both 3 and 5, the result is "FizzBuzz". If the input is divisible by 3 but not 5, the result is "Fizz". If the input is divisible by 5 but not 3, the result is "Buzz". If the input is divisible by neither 3 nor 5, the result is the decimal representation of the input. Implementing the first case as a rudimentary property-based test yields Code 44. Code 4. A naive property-based test for the fizzBuzz function describe("fizzBuzz", () => { context("when the input is divisible by both 3 and 5", () => { it("returns \"FizzBuzz\"", () => { // collect failing inputs (counter-examples) here const counterexamples = []; for (let i = 0; i { context("when divisible by 3 but not by 5", () => { it("returns \"Fizz\"", () => { // collect failing inputs (counter-examples) here const counterexamples = []; for (let i = 0; i { context("when divisible by both 3 and 5", () => { // generator that produces positive integers divisible by 3 and 5 // fc.nat() generates naturals; multiply by 3 and 5 to ensure divisibility const gen = fc.nat().map((n) => n * 3 * 5); it("returns \"FizzBuzz\"", () => { // fc.assert throws if it finds a counter-example fc.assert(fc.property(gen, (n) => { // n is a value generated by gen // return true for success, false for failure return fizzBuzz(n) === "FizzBuzz"; })); }); }); }); Finally, a brief note on writing your own generator. A generator for directed acyclic graphs (DAGs), for example,

Apr 26, 2025 - 08:45

Software Testing: Theory and Practice (Part 5) - How to Select Test Cases

Key Takeaways This Time

There are several approaches to sampling a specification.

In this article we introduce two:

A boundary-value approach (On–Off Point method)
A property-based testing approach

Methods for Sampling a Specification

In previous installments we explained that confirming “the implementation satisfies the specification” often requires an enormous—frequently infinite—number of test cases.

In practice, rather than checking every possible case, we sample the specification, verify behaviour for only a very small subset, and infer behaviour for the rest.

Ways to sample a specification are also called test design techniques, and many techniques have been proposed.

This article introduces the boundary-value approach and the property-based testing approach¹.

Boundary-Value Approach (On–Off Point Method)

The boundary-value approach, Boundary-Value Analysis (BVA), selects inputs called boundary values as samples of the specification.

A boundary value is an input at which the branch executed by the hypothetical implementation changes when it contains conditional statements such as if or switch.

Experience tells us that many defects lurk at boundary values. A typical example is confusing x < y with x ≤ y or vice versa.

In such cases the outputs of x < y and x ≤ y differ only when x = y (here “=” means equality, not assignment). The input satisfying x = y is exactly the boundary value.

Certain assumptions must hold for the boundary-value approach to work as intended.

1. The hypothetical implementation has a top-level conditional branch and is followed only by simple processing that contains no loops or recursion. For example, the function isAdult in Code 1, which takes a non-negative age and returns true if the age is an adult and false otherwise, is a typical case.

Code 1. Hypothetical implementation of isAdult, which determines adulthood

function isAdult(age: number): boolean {
  // NOTE: Written verbosely for clarity instead of “return 20 <= age”
  if (age < 20) return false;
  return true;
}

Placing this assumption keeps the number of samples required for testing to a feasible size.

Conversely, when the processing includes recursion or loops, infinitely many boundary values arise, making it impractical to analyse them all.

What does it mean for “infinitely many boundary values to arise”? Let us examine a counter-example that violates the first assumption. Code 2 shows the hypothetical implementation of a function that returns the i-th Fibonacci number for inputs i that satisfy the pre-condition i ≥ 0.

Like Code 1, it begins with conditional branches, but because it contains recursion afterward, it does not satisfy assumption 1.

Code 2. Hypothetical implementation of a Fibonacci function

function fibonacchi(i: number): number {
  if (i === 0) return 0; // branch for i = 0
  if (i === 1) return 1; // branch for i = 1
  // branch for i ≥ 2; contains recursion
  return fibonacchi(i - 1) + fibonacchi(i - 2);
}

It is easy to see that i = 0 and i = 1 are boundary values, but there are actually boundary values hidden in the recursive part for i ≥ 2.

Consider Code 3, which expands the recursion in Code 2 by one level.

You can see that i = 2 and i = 3 are also boundary values.

Code 3. One-level expansion of the recursion in the Fibonacci function

function fibonacchi(i: number): number {
  if (i === 0) return 0; // branch for i = 0
  if (i === 1) return 1; // branch for i = 1

  // expansion of fibonacchi(i - 1)
  let left: number;
  if ((i - 1) === 0) left = 0;      // branch for i = 1
  else if ((i - 1) === 1) left = 1; // branch for i = 2
  else left = fibonacchi((i - 1) - 1) + fibonacchi((i - 1) - 2);

  // expansion of fibonacchi(i - 2)
  let right: number;
  if ((i - 2) === 0) right = 0;     // branch for i = 2
  else if ((i - 2) === 1) right = 1; // branch for i = 3
  else right = fibonacchi((i - 2) - 1) + fibonacchi((i - 2) - 2);

  return left + right;
}

If you continue unfolding processing that contains recursion or loops in this way, you see boundary values proliferate without bound. Hence assumption 1 is introduced so that the sample size remains manageable.

2. Every conditional expression (the part that decides the branch of an if) in the hypothetical implementation is a linear inequality, or a logical OR, AND, or NOT of linear inequalities. Examples that satisfy this condition are x = 0, 0 < x, 0 ≤ x && x < 100, and x = 0 || y = 0. An example that does not satisfy it is i % 3 === 0.

Boundary Defects

As stated above, many defects lurk at boundary values. Such defects are called boundary bugs.

For example, writing x ≥ 0 where x > 0 is required introduces a boundary bug.

When the conditional expression is a single linear inequality and only one variable is involved, four kinds of boundary bugs are possible²:

Shifted boundary – e.g. writing x > 0 instead of x > 1
Closure defect – e.g. writing x ≤ 0 instead of x < 0
Missing boundary – forgetting to branch where a boundary should exist
Extraneous boundary – introducing a branch where none is needed

To uncover all four types, we select, for every boundary in every conditional branch of the implementation,

an input exactly on the boundary, and
the nearest input on either side of that boundary.

Put differently, we “pick the two closest values that lead to different processing”.

This is Boundary-Value Analysis (the On–Off Point method).

Applied to the earlier isAdult function, boundary-value analysis means testing the cases where age is 19 and 20.

Property-Based Testing

We explained that boundary-value testing requires assumptions about the component’s implementation.

Components that violate those assumptions cannot be tested this way.

For such components I recommend adopting Property-Based Testing (PBT).

We have mentioned PBT in prior installments, but here is a refresher. In traditional Example-Based Testing (EBT), humans choose the inputs.

In contrast, PBT automatically generates inputs. The human supplies a relationship that must hold between input and output, and the output is checked against it.

This relationship is typically a post-condition³. For the FizzBuzz function, for example, we might give the following post-conditions:

If the input is divisible by both 3 and 5, the result is "FizzBuzz".
If the input is divisible by 3 but not 5, the result is "Fizz".
If the input is divisible by 5 but not 3, the result is "Buzz".
If the input is divisible by neither 3 nor 5, the result is the decimal representation of the input.

Implementing the first case as a rudimentary property-based test yields Code 4⁴.

Code 4. A naive property-based test for the fizzBuzz function

describe("fizzBuzz", () => {
  context("when the input is divisible by both 3 and 5", () => {
    it("returns \"FizzBuzz\"", () => {
      // collect failing inputs (counter-examples) here
      const counterexamples = [];

      for (let i = 0; i < 100; i++) {
        // mechanically generate multiples of 3 and 5
        const x = Math.floor(Math.random() * 10000) * 3 * 5;

        // if the output is not "FizzBuzz", add x to counterexamples
        if (fizzBuzz(x) !== "FizzBuzz")
          counterexamples.push(x);
      }

      // expect counterexamples to be empty
      assert.deepStrictEqual(counterexamples, []);
    });
  });

  // ... (other cases)
});

The loop tries 100 inputs, and it is easy to increase or decrease that number, so PBT lets us test far more inputs than traditional example-based tests.

However, the automatically generated inputs often fail to satisfy conditions we actually want—most commonly, the pre-conditions.

There are two approaches to eliminate such unwanted inputs:

Implication approach
Custom generator approach

Implication Approach

As explained in Part 2 (Nov 2024 issue), implication is a logical operator that takes two formulas.

It is written “left ⇒ right” (some people use a double arrow).

Its truth table is shown in Table 1.

Table 1. Truth table of implication

Value of left	Value of right	Value of left ⇒ right
False	False	True
False	True	True
True	False	False
True	True	True

The key point is that the implication is true whenever the left side evaluates to false.

In this approach we put on the left side a formula that returns true for the desired inputs and false otherwise, and we put the test on the right side (Code 5).

For instance, if we wish to treat inputs divisible by 5 as invalid, we can set the left formula to x % 5 === 0. Whenever the pre-condition is false, the entire implication evaluates to true, so the PBT always “passes.”

Code 5. Implementation using implication

describe("fizzBuzz", () => {
  context("when divisible by 3 but not by 5", () => {
    it("returns \"Fizz\"", () => {
      // collect failing inputs (counter-examples) here
      const counterexamples = [];

      for (let i = 0; i < 100; i++) {
        // mechanically generate multiples of 3
        const x = Math.floor(Math.random() * 10000) * 3;

        // if also divisible by 5, treat as pass (the implication’s left side is false)
        if (x % 5 === 0) continue;

        // if the output is not "Fizz", add x to counterexamples
        if (fizzBuzz(x) !== "Fizz")
          counterexamples.push(x);
      }

      // expect counterexamples to be empty
      assert.deepStrictEqual(counterexamples, []);
    });
  });
});

This method is easier than writing a generator and works without relying on any library.

However, because outputs are not checked for inputs that do not satisfy the desired conditions, the actual number of evaluated samples can be smaller than intended.

A serious problem arises when all mechanically generated inputs violate the pre-condition. This situation is called a vacuous truth (often simply vacuous).

If the inputs are vacuous, nothing is really tested. Therefore, when using implication, we should confirm that the generated inputs are not vacuous.

Some PBT libraries offer a filter function that redraws until it finds a sample that makes the predicate true, and they treat vacuous results as test failures.

If available, such filter facilities should be used to avoid vacuity.

Custom Generator Approach

You can also implement your own generator. In PBT libraries, a generator is a component that automatically produces inputs.

When nothing is specified, most libraries choose a default generator that produces arbitrary values of the given type.

If the standard generator produces unwanted inputs, replace it with another generator that yields only the desired ones.

For instance, fast-check⁵, a property-based testing library for JavaScript, allows you to implement a generator by combining existing ones, as in Code 6.

Code 6. Implementation using a generator

import fc from "fast-check";

describe("fizzBuzz", () => {
  context("when divisible by both 3 and 5", () => {
    // generator that produces positive integers divisible by 3 and 5
    // fc.nat() generates naturals; multiply by 3 and 5 to ensure divisibility
    const gen = fc.nat().map((n) => n * 3 * 5);

    it("returns \"FizzBuzz\"", () => {
      // fc.assert throws if it finds a counter-example
      fc.assert(fc.property(gen, (n) => {
        // n is a value generated by gen

        // return true for success, false for failure
        return fizzBuzz(n) === "FizzBuzz";
      }));
    });
  });
});

Finally, a brief note on writing your own generator. A generator for directed acyclic graphs (DAGs), for example, cannot easily be expressed as a combination of existing generators.

One way is to start with an empty graph and repeatedly add either

a node with no parents, or
a new node whose parents are one or more existing nodes chosen at random.

We omitted Equivalence Class Partitioning (ECP). Many definitions of ECP lack theoretical grounding, and those that do have a proper basis are too intricate to explain here. ↩
These are the one-dimensional cases. In two dimensions, boundary tilt is added to the list (Software Testing Techniques, 2nd Edition, Boris Beizer). ↩
When the post-condition cannot be stated succinctly, we sometimes give simpler relationships. For instance, the post-condition for addition over naturals is cumbersome to express explicitly; instead, we often supply multiple simpler laws such as commutativity (swapping the first and second operands leaves the result unchanged). ↩
The code examples below are intentionally simple and eschew libraries. In practice you would use a dedicated PBT library. ↩
https://fast-check.dev/ ↩