Radix Sort

Radix Sort is a sorting algorithm that works by sorting numbers based on their digits, starting from the least significant digit (rightmost) to the most significant digit (leftmost). Let’s say we have an array: [321, 232, 464, 45, 0, 55, 689] 1. First, we sort the numbers based on the units place (1s digit). 2. Next, we sort based on the tens place (10s digit). 3. Finally, we sort based on the hundreds place (100s digit). This process continues for each digit position until the entire array is sorted. Note : Please go through the counting sort before reading this article because counting sort is used as an intermediate sort in radix sort. Let the initial array be [321, 232, 464, 45, 0, 55, 689]. It is sorted according to radix sort as shown in the figure below. Working of Radix Sort Find the largest element in the array, i.e. max. Let X be the number of digits in max. X is calculated because we have to go through all the significant places of all elements. In this array [321, 232, 464, 45, 0, 55, 689], we have the largest number 689. It has 3 digits. Therefore, the loop should go up to hundreds place (3 times). 2.Now, process each digit position (starting from the least significant place). Use any stable sorting algorithm (like Counting Sort) to sort the elements based on the digit at the current place value. For example, to sort based on the unit place digit (place = 1): First, calculate the count of each digit (0–9). Then, compute the cumulative count. Finally, place each element in the output array based on its unit digit using the cumulative count. This ensures the numbers are stably sorted at this digit position before moving to the next (e.g., tens, hundreds, etc.). 3. Now, sort the elements based on digits at tens place. 4. Finally, sort the elements based on the digits at hundreds place 5. So, Final Sorted array is: Radix Sort Algorithm FUNCTION CountingSortForRadix(arr, place): n ← length of arr output ← array of size n, initialized with 0 count ← array of size 10, initialized with 0 // Count occurrences of each digit at current place FOR i ← 0 TO n - 1: digit ← (arr[i] DIV place) MOD 10 count[digit] ← count[digit] + 1 // Compute cumulative count FOR i ← 1 TO 9: count[i] ← count[i] + count[i - 1] // Build the output array FOR i ← n - 1 DOWNTO 0: digit ← (arr[i] DIV place) MOD 10 output[count[digit] - 1] ← arr[i] count[digit] ← count[digit] - 1 // Copy output to original array FOR i ← 0 TO n - 1: arr[i] ← output[i] END FUNCTION FUNCTION RadixSort(arr): max ← maximum value in arr place ← 1 WHILE (max DIV place) > 0: CountingSortForRadix(arr, place) place ← place * 10 RETURN arr END FUNCTION Radix Sort Code function countingSortForRadix(arr, place) { const n = arr.length; let output = new Array(n).fill(0); let count = new Array(10).fill(0); // Count occurrences of each digit at "place" for (let i = 0; i

May 1, 2025 - 11:28

Radix Sort is a sorting algorithm that works by sorting numbers based on their digits, starting from the least significant digit (rightmost) to the most significant digit (leftmost).

Let’s say we have an array:
[321, 232, 464, 45, 0, 55, 689]

1. First, we sort the numbers based on the units place (1s digit).

2. Next, we sort based on the tens place (10s digit).

3. Finally, we sort based on the hundreds place (100s digit).

This process continues for each digit position until the entire array is sorted.

Note : Please go through the counting sort before reading this article because counting sort is used as an intermediate sort in radix sort.

Let the initial array be [321, 232, 464, 45, 0, 55, 689]. It is sorted according to radix sort as shown in the figure below.

Working of Radix Sort

Find the largest element in the array, i.e. max. Let X be the number of digits in max. X is calculated because we have to go through all the significant places of all elements.

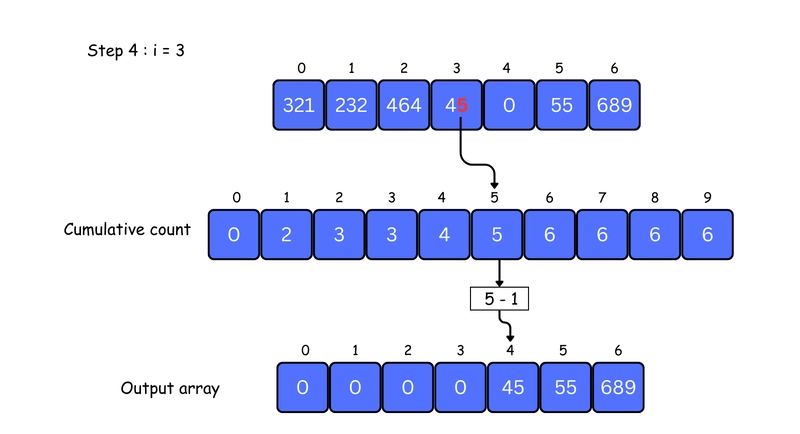
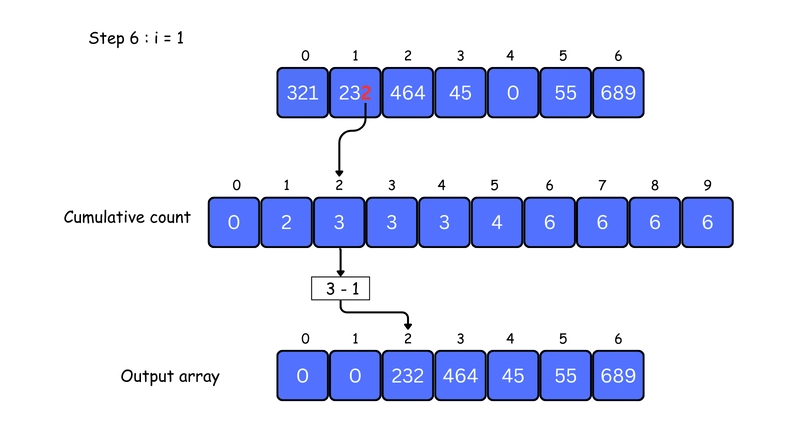
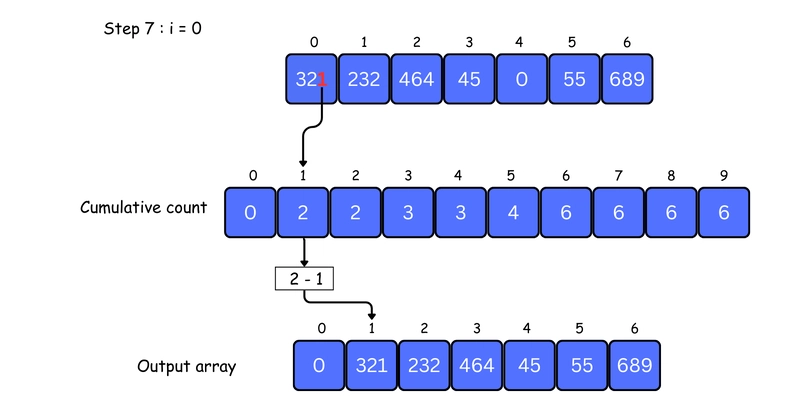
In this array [321, 232, 464, 45, 0, 55, 689], we have the largest number 689. It has 3 digits. Therefore, the loop should go up to hundreds place (3 times).

2.Now, process each digit position (starting from the least significant place).

Use any stable sorting algorithm (like Counting Sort) to sort the elements based on the digit at the current place value.

For example, to sort based on the unit place digit (place = 1):

First, calculate the count of each digit (0–9).
Then, compute the cumulative count.
Finally, place each element in the output array based on its unit digit using the cumulative count.
This ensures the numbers are stably sorted at this digit position before moving to the next (e.g., tens, hundreds, etc.).

3. Now, sort the elements based on digits at tens place.

4. Finally, sort the elements based on the digits at hundreds place

5. So, Final Sorted array is:

Radix Sort Algorithm

FUNCTION CountingSortForRadix(arr, place):
    n ← length of arr
    output ← array of size n, initialized with 0
    count ← array of size 10, initialized with 0

    // Count occurrences of each digit at current place
    FOR i ← 0 TO n - 1:
        digit ← (arr[i] DIV place) MOD 10
        count[digit] ← count[digit] + 1

    // Compute cumulative count
    FOR i ← 1 TO 9:
        count[i] ← count[i] + count[i - 1]

    // Build the output array
    FOR i ← n - 1 DOWNTO 0:
        digit ← (arr[i] DIV place) MOD 10
        output[count[digit] - 1] ← arr[i]
        count[digit] ← count[digit] - 1

    // Copy output to original array
    FOR i ← 0 TO n - 1:
        arr[i] ← output[i]
END FUNCTION

FUNCTION RadixSort(arr):
    max ← maximum value in arr

    place ← 1
    WHILE (max DIV place) > 0:
        CountingSortForRadix(arr, place)
        place ← place * 10

    RETURN arr
END FUNCTION

Radix Sort Code

function countingSortForRadix(arr, place) {
  const n = arr.length;
  let output = new Array(n).fill(0);
  let count = new Array(10).fill(0);

  // Count occurrences of each digit at "place"
  for (let i = 0; i < n; i++) {
    let digit = Math.floor(arr[i] / place) % 10;
    count[digit]++;
  }

  // Compute cumulative count
  for (let i = 1; i < 10; i++) {
    count[i] += count[i - 1];
  }

  // Build the output array (placing elements in sorted order)
  for (let i = n - 1; i >= 0; i--) {
    let digit = Math.floor(arr[i] / place) % 10;
    output[count[digit] - 1] = arr[i];
    count[digit]--;
  }

  // Copy sorted values back to arr
  for (let i = 0; i < n; i++) {
    arr[i] = output[i];
  }
}

function radixSort(arr) {
  let max = Math.max(...arr);

  // Apply counting sort for each digit place (1s, 10s, 100s, etc.)
  for (let place = 1; Math.floor(max / place) > 0; place *= 10) {
    countingSortForRadix(arr, place);
  }

  return arr;
}

// Example Usage
const inputArray = [321, 232, 464, 45, 0, 55, 689];
console.log("Sorted Array:", radixSort(inputArray));

Radix Sort Complexity

Time Complexity
Best	O(n+k)
Worst	O(n+k)
Average	O(n+k)
Space Complexity	O(max)
Stability	Yes

Since radix sort is a non-comparative algorithm, it has advantages over comparative sorting algorithms.

For the radix sort that uses counting sort as an intermediate stable sort, the time complexity is O(d(n+k)).

Here, d is the number cycle and O(n+k) is the time complexity of counting sort.

Thus, radix sort has linear time complexity which is better than O(nlog n) of comparative sorting algorithms.

If we take very large digit numbers or the number of other bases like 32-bit and 64-bit numbers then it can perform in linear time however the intermediate sort takes large space.

This makes radix sort space inefficient. This is the reason why this sort is not used in software libraries.

Applications of Radix Sort:

✅ 1. Sorting Large Sets of Integers
Radix Sort performs well when sorting large numbers of integers that have a fixed number of digits (e.g. phone numbers, zip codes, IDs). It's faster than comparison-based sorts in these cases.

✅ 2. Sorting Strings or Words (Fixed Length)
Radix Sort can be adapted to sort strings (like words or names) character by character, especially when they are of the same length — such as:

Sorting dictionary entries
Autocomplete suggestions

✅ 3. Used in Data Processing Systems
Systems that handle large volumes of numeric data (like logs, telemetry, sensor data) use radix sort for its linear-time efficiency.

✅ 4. Digital Systems / Embedded Devices
In low-memory or performance-critical environments, Radix Sort is used to sort data like:

Sensor readings
Timestamp logs
Signal values

✅ 5. Databases and Indexing
Some databases or file systems may use radix-like logic to quickly index and sort keys, especially when keys are numeric or fixed-length strings.

✅ 6. Graphics and Image Processing
Used in GPU sorting tasks (like depth sorting or bucket-based rendering) due to its predictable performance and parallelizability.