Invert Binary Tree in Java

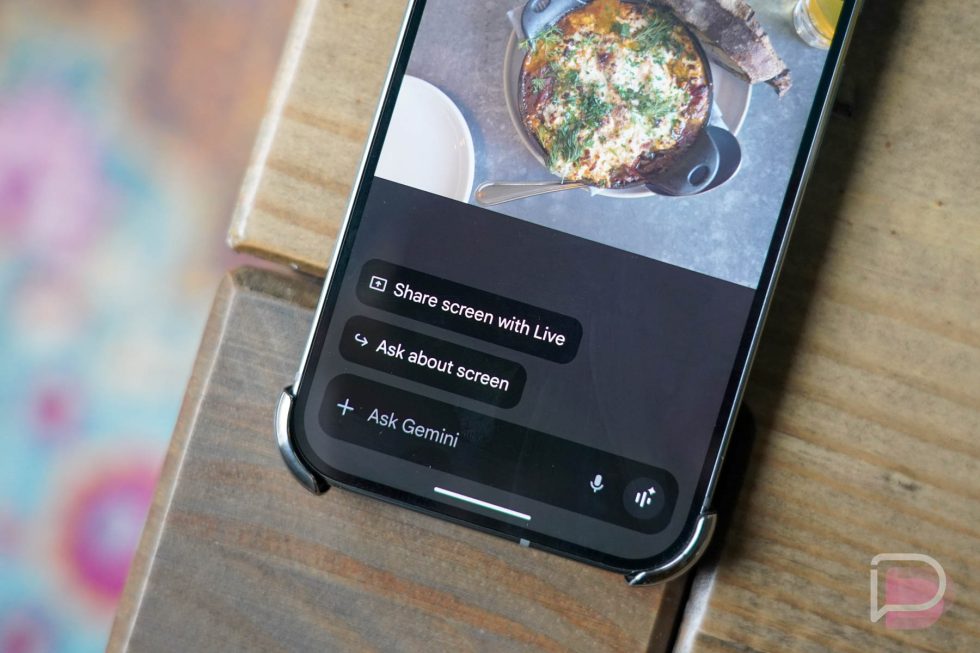
Invert Binary Tree - A Step-by-Step Journey Binary trees are a fascinating data structure, and problems involving them often show up in coding interviews. Today, I’ll walk you through my solution to LeetCode 226: Invert Binary Tree, an "Easy" problem that’s perfect for understanding tree traversal and manipulation. Let’s dive in! The Problem You’re given the root of a binary tree, and your task is to invert it—essentially, swap every left child with its right child, all the way down the tree. The root stays where it is, but its subtrees get flipped. Here are the examples provided: Example 1: Input: [4,2,7,1,3,6,9] Output: [4,7,2,9,6,3,1] Visualize it: The tree with 4 at the root has left subtree [2,1,3] and right subtree [7,6,9]. After inverting, it becomes [4,7,2,9,6,3,1]. Example 2: Input: [2,1,3] Output: [2,3,1] Example 3: Input: [] Output: [] The constraints tell us the tree can have 0 to 100 nodes, and node values range from -100 to 100. Simple enough, right? Let’s solve it. My Initial Thoughts When I first saw this problem, I thought about how to visit every node in the tree exactly once and swap its left and right children. This screams tree traversal! There are two classic approaches: recursive (depth-first) and iterative (breadth-first or depth-first with a stack/queue). Recursion might be the most intuitive for trees, but I decided to go with an iterative solution using a queue—partly to mix things up and partly because it aligns with a breadth-first search (BFS) mindset. Let’s see how it works. The Solution Here’s my code in Java: /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode invertTree(TreeNode root) { if (root == null) { return root; } // Handle empty tree Deque queue = new ArrayDeque(); queue.offerLast(root); // Start with the root while (!queue.isEmpty()) { TreeNode curr = queue.pollFirst(); // Get the next node // Swap left and right children TreeNode tmp = curr.left; curr.left = curr.right; curr.right = tmp; // Add children to queue if they exist if (curr.left != null) { queue.offerLast(curr.left); } if (curr.right != null) { queue.offerLast(curr.right); } } return root; // Return the modified tree } } How It Works Base Case: If the root is null (empty tree), return it as-is. This handles Example 3 and prevents null pointer issues. Queue Setup: I use a Deque (double-ended queue) as a regular queue via offerLast and pollFirst. We start by adding the root node. BFS Traversal: While the queue isn’t empty: Pop the front node (curr). Swap its left and right children using a temporary variable (tmp). If the (now-swapped) left child exists, add it to the queue. If the (now-swapped) right child exists, add it to the queue. Return: Once the queue is empty, all nodes have been visited and inverted. Return the root. This approach processes the tree level by level, which is what makes it BFS. For Example 1: Start with 4. Swap 2 and 7 → [4,7,2]. Process 7. Swap 6 and 9 → [4,7,2,9,6]. Process 2. Swap 1 and 3 → [4,7,2,9,6,3,1]. Done! Time and Space Complexity Time Complexity: O(n), where n is the number of nodes. We visit each node exactly once. Space Complexity: O(w), where w is the maximum width of the tree (the most nodes at any level). In the worst case (a complete binary tree), this could be O(n/2) ≈ O(n), but typically it’s less. Why BFS Over Recursion? You might wonder why I didn’t go with the recursive solution, which is shorter: public TreeNode invertTree(TreeNode root) { if (root == null) return root; TreeNode left = invertTree(root.left); TreeNode right = invertTree(root.right); root.left = right; root.right = left; return root; } The recursive version is elegant and leverages the tree’s natural structure. It’s DFS (post-order, technically), and it’s often the go-to for tree problems. But I chose BFS because: It’s less common for this problem, making it a fun twist. It demonstrates queue-based traversal, a useful skill for other problems (e.g., level-order traversal). It avoids stack overflow risks in extremely deep trees (though unlikely within the constraints). Testing It Out Let’s verify with the examples: [4,2,7,1,3,6,9] → Queue processes 4, then 7 and 2, then 9, 6, 3, 1 → [4,7,2,9,6,3,1]. Check! [2,1,3] → Swap 1 and 3 → [2,3,1]. Check! []

Mar 15, 2025 - 04:32

Invert Binary Tree - A Step-by-Step Journey

Binary trees are a fascinating data structure, and problems involving them often show up in coding interviews. Today, I’ll walk you through my solution to LeetCode 226: Invert Binary Tree, an "Easy" problem that’s perfect for understanding tree traversal and manipulation. Let’s dive in!

The Problem

You’re given the root of a binary tree, and your task is to invert it—essentially, swap every left child with its right child, all the way down the tree. The root stays where it is, but its subtrees get flipped. Here are the examples provided:

Example 1:

  Input: [4,2,7,1,3,6,9]
  Output: [4,7,2,9,6,3,1]

Visualize it: The tree with 4 at the root has left subtree [2,1,3] and right subtree [7,6,9]. After inverting, it becomes [4,7,2,9,6,3,1].

Example 2:

  Input: [2,1,3]
  Output: [2,3,1]

Example 3:

  Input: []
  Output: []

The constraints tell us the tree can have 0 to 100 nodes, and node values range from -100 to 100. Simple enough, right? Let’s solve it.

My Initial Thoughts

When I first saw this problem, I thought about how to visit every node in the tree exactly once and swap its left and right children. This screams tree traversal! There are two classic approaches: recursive (depth-first) and iterative (breadth-first or depth-first with a stack/queue). Recursion might be the most intuitive for trees, but I decided to go with an iterative solution using a queue—partly to mix things up and partly because it aligns with a breadth-first search (BFS) mindset. Let’s see how it works.

The Solution

Here’s my code in Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) { return root; } // Handle empty tree

        Deque<TreeNode> queue = new ArrayDeque<>();
        queue.offerLast(root); // Start with the root

        while (!queue.isEmpty()) {
            TreeNode curr = queue.pollFirst(); // Get the next node
            // Swap left and right children
            TreeNode tmp = curr.left;
            curr.left = curr.right;
            curr.right = tmp;

            // Add children to queue if they exist
            if (curr.left != null) {
                queue.offerLast(curr.left);
            }
            if (curr.right != null) {
                queue.offerLast(curr.right);
            }
        }
        return root; // Return the modified tree
    }
}

How It Works

Base Case: If the root is null (empty tree), return it as-is. This handles Example 3 and prevents null pointer issues.
Queue Setup: I use a Deque (double-ended queue) as a regular queue via offerLast and pollFirst. We start by adding the root node.
BFS Traversal: While the queue isn’t empty:
- Pop the front node (curr).
- Swap its left and right children using a temporary variable (tmp).
- If the (now-swapped) left child exists, add it to the queue.
- If the (now-swapped) right child exists, add it to the queue.
Return: Once the queue is empty, all nodes have been visited and inverted. Return the root.

This approach processes the tree level by level, which is what makes it BFS. For Example 1:

Start with 4. Swap 2 and 7 → [4,7,2].
Process 7. Swap 6 and 9 → [4,7,2,9,6].
Process 2. Swap 1 and 3 → [4,7,2,9,6,3,1].
Done!

Time and Space Complexity

Time Complexity: O(n), where n is the number of nodes. We visit each node exactly once.
Space Complexity: O(w), where w is the maximum width of the tree (the most nodes at any level). In the worst case (a complete binary tree), this could be O(n/2) ≈ O(n), but typically it’s less.

Why BFS Over Recursion?

You might wonder why I didn’t go with the recursive solution, which is shorter:

public TreeNode invertTree(TreeNode root) {
    if (root == null) return root;
    TreeNode left = invertTree(root.left);
    TreeNode right = invertTree(root.right);
    root.left = right;
    root.right = left;
    return root;
}

The recursive version is elegant and leverages the tree’s natural structure. It’s DFS (post-order, technically), and it’s often the go-to for tree problems. But I chose BFS because:

It’s less common for this problem, making it a fun twist.
It demonstrates queue-based traversal, a useful skill for other problems (e.g., level-order traversal).
It avoids stack overflow risks in extremely deep trees (though unlikely within the constraints).

Testing It Out

Let’s verify with the examples:

[4,2,7,1,3,6,9] → Queue processes 4, then 7 and 2, then 9, 6, 3, 1 → [4,7,2,9,6,3,1]. Check!
[2,1,3] → Swap 1 and 3 → [2,3,1]. Check!
[] → Return []. Check!

Lessons Learned

This problem taught me:

The power of swapping pointers directly in a tree.
How BFS can solve problems beyond just traversal.
The trade-offs between iterative and recursive approaches.

Next time, I might explore a DFS iterative solution with a stack for comparison. But for now, this BFS approach feels satisfyingly complete.

Conclusion

"Invert Binary Tree" is a great problem to build intuition for tree manipulation. Whether you go recursive or iterative, the key is understanding how to traverse and modify the structure. I hope my BFS-based solution sparks some curiosity—try it out, tweak it, and let me know what you think!

Happy coding!