GeeksforGeeks : M Coloring Problem

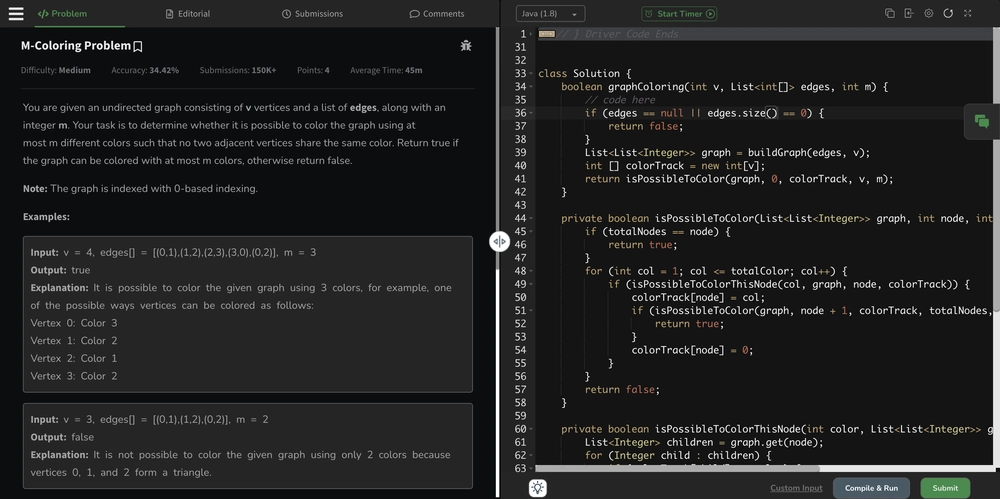
Problem https://www.geeksforgeeks.org/problems/m-coloring-problem-1587115620/1 You are given an undirected graph consisting of v vertices and a list of edges, along with an integer m. Your task is to determine whether it is possible to color the graph using at most m different colors such that no two adjacent vertices share the same color. Return true if the graph can be colored with at most m colors, otherwise return false. Note: The graph is indexed with 0-based indexing. Examples Input: v = 4, edges[] = [(0,1),(1,2),(2,3),(3,0),(0,2)], m = 3 Output: true Explanation: It is possible to color the given graph using 3 colors, for example, one of the possible ways vertices can be colored as follows: Vertex 0: Color 3 Vertex 1: Color 2 Vertex 2: Color 1 Vertex 3: Color 2 Input: v = 3, edges[] = [(0,1),(1,2),(0,2)], m = 2 Output: false Explanation: It is not possible to color the given graph using only 2 colors because vertices 0, 1, and 2 form a triangle. Expected Time Complexity: O(mV) Expected Auxiliary Space: O(v2) Constraints 1 ≤ v ≤ 20 1 ≤ edges.size() ≤ (v*(v-1))/2 0 ≤ edges[i][j] ≤ n-1 1 ≤ m ≤ v Intuition For each of the nodes, we need to put the colors such that, if we look at the neighbours of every node, they should not be equal. This means, once we apply a color, say colorA, to the 0th node, all the children or neighbours of the 0th node shouldn't be colorA. This must hold true for all the nodes, and we can try all possibilities of color combinations and see if any of the combinations are suitable for our scenario. Thus, we can recursively try every combination, and if one combination holds, then we return true. If none of the combination holds, then return false. Approach Build the graph using an adjacency list representation. Start coloring from the first node, say the 0th node. Try all the m combinations of color on the 0th node, where we will be checking if any of the neighbours have having same color. If not, then we will color the 0th node with say colorA and move to the next node, ie 1st node. This is repeated until the last node. Time and Space Complexity O(V + E) for building graph O(E) for the isPossibleToColorThisNode method checks whether a neighbour has the same color. O(M^V) for trying all combinations for each vertex. So total time complexity: O(M^V). Space Complexity : O(V) + O(recursion stack spaces) Code class Solution { boolean graphColoring(int v, List edges, int m) { // code here if (edges == null || edges.size() == 0) { return false; } List graph = buildGraph(edges, v); int [] colorTrack = new int[v]; return isPossibleToColor(graph, 0, colorTrack, v, m); } private boolean isPossibleToColor(List graph, int node, int [] colorTrack, int totalNodes, int totalColor) { if (totalNodes == node) { return true; } for (int col = 1; col

Mar 29, 2025 - 15:28

Problem

https://www.geeksforgeeks.org/problems/m-coloring-problem-1587115620/1

You are given an undirected graph consisting of v vertices and a list of edges, along with an integer m. Your task is to determine whether it is possible to color the graph using at most m different colors such that no two adjacent vertices share the same color. Return true if the graph can be colored with at most m colors, otherwise return false.

Note: The graph is indexed with 0-based indexing.

Examples

Input: v = 4, edges[] = [(0,1),(1,2),(2,3),(3,0),(0,2)], m = 3
Output: true
Explanation: It is possible to color the given graph using 3 colors, for example, one of the possible ways vertices can be colored as follows:
Vertex 0: Color 3
Vertex 1: Color 2
Vertex 2: Color 1
Vertex 3: Color 2

Input: v = 3, edges[] = [(0,1),(1,2),(0,2)], m = 2
Output: false
Explanation: It is not possible to color the given graph using only 2 colors because vertices 0, 1, and 2 form a triangle.
Expected Time Complexity: O(mV)
Expected Auxiliary Space: O(v2)

Constraints

1 ≤ v ≤ 20
1 ≤ edges.size() ≤ (v*(v-1))/2
0 ≤ edges[i][j] ≤ n-1
1 ≤ m ≤ v

Intuition

For each of the nodes, we need to put the colors such that, if we look at the neighbours of every node, they should not be equal. This means, once we apply a color, say colorA, to the 0th node, all the children or neighbours of the 0th node shouldn't be colorA.
This must hold true for all the nodes, and we can try all possibilities of color combinations and see if any of the combinations are suitable for our scenario.
Thus, we can recursively try every combination, and if one combination holds, then we return true. If none of the combination holds, then return false.

Approach

Build the graph using an adjacency list representation.
Start coloring from the first node, say the 0th node.
Try all the m combinations of color on the 0th node, where we will be checking if any of the neighbours have having same color. If not, then we will color the 0th node with say colorA and move to the next node, ie 1st node.
This is repeated until the last node.

Time and Space Complexity

O(V + E) for building graph
O(E) for the isPossibleToColorThisNode method checks whether a neighbour has the same color.
O(M^V) for trying all combinations for each vertex.

So total time complexity: O(M^V).

Space Complexity : O(V) + O(recursion stack spaces)

Code

class Solution {
    boolean graphColoring(int v, List<int[]> edges, int m) {
        // code here
        if (edges == null || edges.size() == 0) {
            return false;
        }
        List<List<Integer>> graph = buildGraph(edges, v);
        int [] colorTrack = new int[v];
        return isPossibleToColor(graph, 0, colorTrack, v, m);
    }

    private boolean isPossibleToColor(List<List<Integer>> graph, int node, int [] colorTrack, int totalNodes, int totalColor) {
        if (totalNodes == node) {
            return true;
        }
        for (int col = 1; col <= totalColor; col++) {
            if (isPossibleToColorThisNode(col, graph, node, colorTrack)) {
                colorTrack[node] = col;
                if (isPossibleToColor(graph, node + 1, colorTrack, totalNodes, totalColor)) {
                    return true;
                }
                colorTrack[node] = 0;
            }
        }
        return false;
    }

    private boolean isPossibleToColorThisNode(int color, List<List<Integer>> graph, int node, int [] colorTrack) {
        List<Integer> children = graph.get(node);
        for (Integer child : children) {
            if (colorTrack[child] == color) {
                return false;
            }
        }
        return true;
    }

    private List<List<Integer>> buildGraph(List<int[]> edges, int n) {
        List<List<Integer>> graph = new ArrayList<>();
        for (int node = 0; node < n; node++) {
            graph.add(new ArrayList<>());
        }
        for (int [] edge : edges) {
            graph.get(edge[0]).add(edge[1]);
            graph.get(edge[1]).add(edge[0]);
        }
        return graph;
    }
}