Finds the shortest path on a 2D grid (with obstacles) using the A* search algorithm.

# Find Best Path in 2D Grid with Obstacles - A* Search Algorithm # Description: Finds the shortest path on a 2D grid (with obstacles) using the A* search algorithm. import heapq def manhattan_distance(point_a, point_b): """ Calculate the Manhattan distance between two points. Args: point_a (tuple): First point (row, col) point_b (tuple): Second point (row, col) Returns: int: Manhattan distance between the points """ return abs(point_a[0] - point_b[0]) + abs(point_a[1] - point_b[1]) def is_valid_move(grid, point): """ Check if a point is a valid move on the grid. Args: grid (list of list): 2D grid where 1 represents obstacles point (tuple): Point to check (row, col) Returns: bool: True if the point is a valid move, False otherwise """ row, col = point return (0

Mar 28, 2025 - 04:49

Finds the shortest path on a 2D grid (with obstacles) using the A* search algorithm.

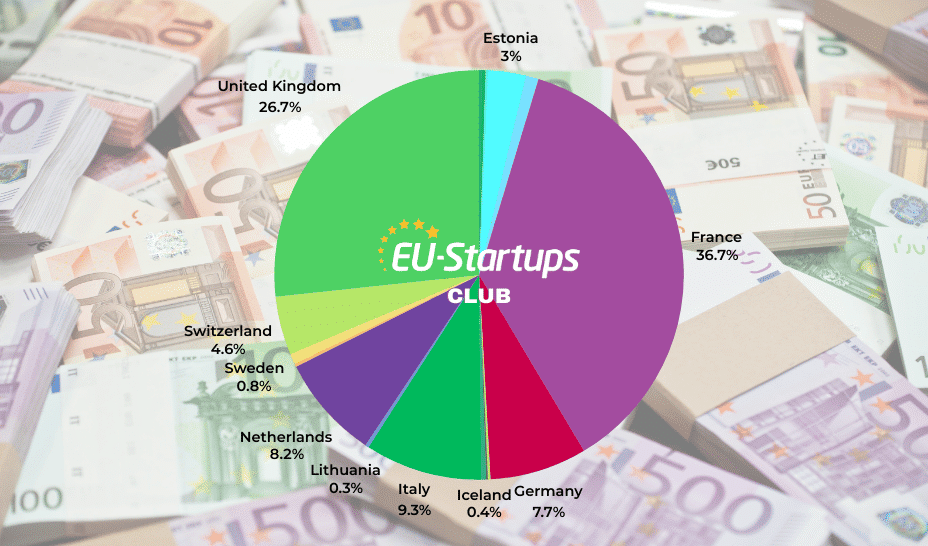
# Find Best Path in 2D Grid with Obstacles - A* Search Algorithm
# Description: Finds the shortest path on a 2D grid (with obstacles) using the A* search algorithm.

import heapq

def manhattan_distance(point_a, point_b):
    """
    Calculate the Manhattan distance between two points.

    Args:
        point_a (tuple): First point (row, col)
        point_b (tuple): Second point (row, col)

    Returns:
        int: Manhattan distance between the points
    """
    return abs(point_a[0] - point_b[0]) + abs(point_a[1] - point_b[1])

def is_valid_move(grid, point):
    """
    Check if a point is a valid move on the grid.

    Args:
        grid (list of list): 2D grid where 1 represents obstacles
        point (tuple): Point to check (row, col)

    Returns:
        bool: True if the point is a valid move, False otherwise
    """
    row, col = point
    return (0 <= row < len(grid) and 
            0 <= col < len(grid[0]) and 
            grid[row][col] != 1)

def reconstruct_path(came_from, current):
    """
    Reconstruct the path from start to goal.

    Args:
        came_from (dict): Dictionary tracking the previous point for each point
        current (tuple): Goal point

    Returns:
        list: Path from start to goal
    """
    path = [current]
    while current in came_from:
        current = came_from[current]
        path.append(current)
    return path[::-1]

def a_star(start, goal, grid):
    """
    Find the shortest path in a 2D grid using A* search algorithm.

    Args:
        start (tuple): Starting point (row, col)
        goal (tuple): Goal point (row, col)
        grid (list of list): 2D grid where 1 represents obstacles

    Returns:
        list or str: Path from start to goal, or "No path found"

    Example:
        grid = [
            [0, 0, 0, 0],
            [0, 1, 1, 0],
            [0, 0, 0, 0],
            [0, 1, 0, 0]
        ]
        start = (0, 0)
        goal = (3, 3)
        path = a_star(start, goal, grid)
    """
    # Possible movement directions: right, down, left, up
    DIRECTIONS = [(0, 1), (1, 0), (0, -1), (-1, 0)]

    # Priority queue to store nodes to explore
    # Format: (f_score, g_score, point)
    open_set = []
    heapq.heappush(open_set, (manhattan_distance(start, goal), 0, start))

    # Track the path and movement costs
    came_from = {}
    g_score = {start: 0}

    while open_set:
        # Get the node with the lowest f_score
        _, current_cost, current = heapq.heappop(open_set)

        # Check if we've reached the goal
        if current == goal:
            return reconstruct_path(came_from, current)

        # Explore neighboring cells
        for dx, dy in DIRECTIONS:
            neighbor = (current[0] + dx, current[1] + dy)

            # Skip invalid moves
            if not is_valid_move(grid, neighbor):
                continue

            # Calculate tentative movement cost
            tentative_cost = current_cost + 1

            # Update if this is a better path
            if neighbor not in g_score or tentative_cost < g_score[neighbor]:
                came_from[neighbor] = current
                g_score[neighbor] = tentative_cost

                # Calculate f_score (total estimated cost)
                f_score = tentative_cost + manhattan_distance(neighbor, goal)
                heapq.heappush(open_set, (f_score, tentative_cost, neighbor))

    # No path found
    return "No path found"