Empowering LLMs to Think Deeper by Erasing Thoughts

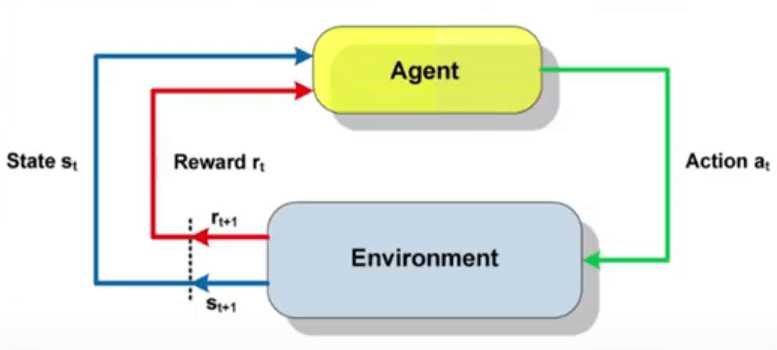
Introduction Recent large language models (LLMs) — such as OpenAI’s o1/o3, DeepSeek’s R1 and Anthropic’s Claude 3.7 — demonstrate that allowing the model to think deeper and longer at test time can significantly enhance model’s reasoning capability. The core approach underlying their deep thinking capability is called chain-of-thought (CoT), where the model iteratively generates intermediate […] The post Empowering LLMs to Think Deeper by Erasing Thoughts appeared first on Towards Data Science.

May 13, 2025 - 01:32

Empowering LLMs to Think Deeper by Erasing Thoughts

Introduction

Recent large language models (LLMs) — such as OpenAI’s o1/o3, DeepSeek’s R1 and Anthropic’s Claude 3.7 — demonstrate that allowing the model to think deeper and longer at test time can significantly enhance model’s reasoning capability. The core approach underlying their deep thinking capability is called chain-of-thought (CoT), where the model iteratively generates intermediate reasoning steps and appends them to the current context until producing the final answer.

However, as tasks become increasingly complex, the steps needed to solve them grow dramatically. For instance, consider solving NP-hard problems using CoT — the reasoning trace would inevitably span exponential steps, assuming a fixed-size Transformer as the base model and P ≠ NP. This raises an important question:

Will CoT-based test-time scaling hit hard ceilings?

Unfortunately, probably yes. Various limitations will emerge for harder tasks: (1) chains will inevitably exceed model’s context windows, (2) critical information becomes buried and nearly impossible to retrieve from numerous preceding tokens, and (3) the self-attention complexity makes generating each new token prohibitively expensive.

Generated by ChatGPT, prompted by author

In this article, we challenge the conventional “write-only” CoT reasoning paradigm that dominates current LLM architectures, from both theoretical and practical perspectives. Furthermore, we will explore a fundamentally different reasoning approach that allows LLM to not only generate thoughts, but also erase thoughts. This capacity for thought erasure not only offers significant practical benefits in performance and efficiency, but proves fundamental for achieving optimal reasoning efficiency from a computational theory perspective.

This post is based on the paper C. Yang et al., “PENCIL: Long thoughts with short memory” accepted in International Conference on Machine Learning 2025, a collaboration with Nathan Srebro, David McAllester, Zhiyuan Li. Code is also available.

Not Everything Needs to Be Remembered

The idea of selectively discarding information has deep roots in computer science history, from the earliest computational models to modern systems. The classic Turing machine overwrites symbols on its tape rather than preserving every state; programming languages reclaim memory through stack frames that are automatically released when functions complete their execution; and modern garbage collectors continuously identify and remove objects no longer accessible to the program. These mechanisms weren’t merely efficiency optimizations — they were essential design choices that made complex computation possible within finite resources.

This idea also applies to human reasoning. In theorem proving, once a lemma is established, we discard its detailed derivation while preserving the result; when exploring problem-solving approaches, we simply mark unproductive paths as “failed” without retaining their full traces. Throughout complex reasoning, we naturally compress information, retaining conclusions while discarding the scaffolding used to reach them.

PENCIL: A New Reasoning Paradigm

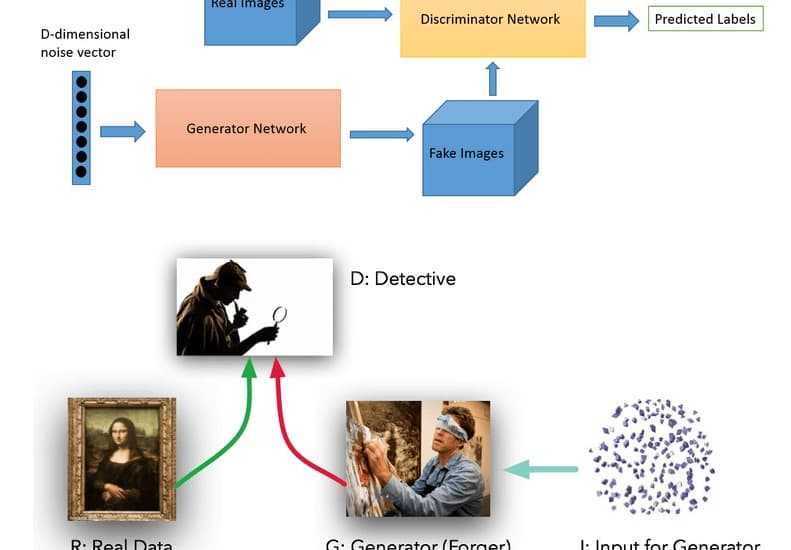
Therefore, we propose PENCIL, a new reasoning paradigm for LLMs. Unlike CoT that only generates thoughts, PENCIL recursively generates and erases thoughts until reaching the final answer. It maintains only the minimal context required for generating future thoughts, so the model can think longer and deeper to solve harder tasks using shorter working memory. The following figure illustrates how PENCIL works

Chain-of-Thought (left) preserves all reasoning steps in context, creating lengthy outputs. PENCIL (right) alternates between generation (bold) and reduction (blue): discarding intermediate thoughts when no longer needed. After reaching the solution, PENCIL returns only the final answer, hiding the thinking process.

How Do Models Erase Thoughts?

PENCIL’s erasure mechanism draws on two classical ideas. First, from rewriting rules in logic and classical automated theorem proving, which continuously apply predefined rules to simplify complex logical or arithmetic expressions into canonical forms until reaching a final answer. Second, from functional programming languages, which creates stack frames to store local variables when calling functions and releases corresponding memory when functions return, automatically discarding intermediate states that are no longer needed.

Specifically, we introduce three special tokens, called [CALL], [SEP], and [RETURN], and use the following reduction rule to implement erasure:

where C stands for context, T stands for intermediate thoughts, and A stands for answer. Whenever the generated sequence completely matches the pattern on the left, PENCIL triggers the reduction rule, erasing thoughts and merging the answer back into the context. It is important to note that C, T and A can themselves contain special tokens, thereby supporting recursive structures similar to nested function calls — for example, C may contain another [CALL] token, indicating that a new thinking subroutine has been initiated.

How to Use PENCIL?

PENCIL’s erasure mechanism flexibly supports various reasoning patterns, such as:

1⃣ Task Decomposition: Using [CALL] to initiate subproblems, generate intermediate results, and then use [SEP] and [RETURN] to merge outputs and erase subproblem reasoning details;

2⃣ Branch and Backtrack: Using a [CALL], [SEP], [RETURN] triplet to manage an exploration branch in a search tree, erasing invalid paths upon conflicts or failures.

3⃣ Summarization / Tail Recursion: Condensing a lengthy reasoning trace into concise summary, similar to tail recursion optimization in programming:

where T represents the original complex reasoning process (or a more difficult problem), and T’ represents the summarized or simplified content (or an equivalent, more tractable problem).

Example on a NP-Complete Task

For example, consider a classic NP-Complete problem Boolean Satisfiability (SAT): given a Boolean formula, determine whether there exists a variable assignment that makes it true. This problem is (widely believed to) require exponential time but only polynomial space to solve, with the simplest approach being traversing a binary search tree of depth n.

Traditional CoT would accumulate intermediate calculations, causing the context length to grow proportionally with the number of nodes in the search tree, which is exponential time complexity of O(2^n). In comparison, PENCIL can recursively branch to try True/False for a variable, backtracking upon conflict and erasing all thoughts within that branch. This thus keeps the context length proportional to the search depth, which is space complexity of only O(n).

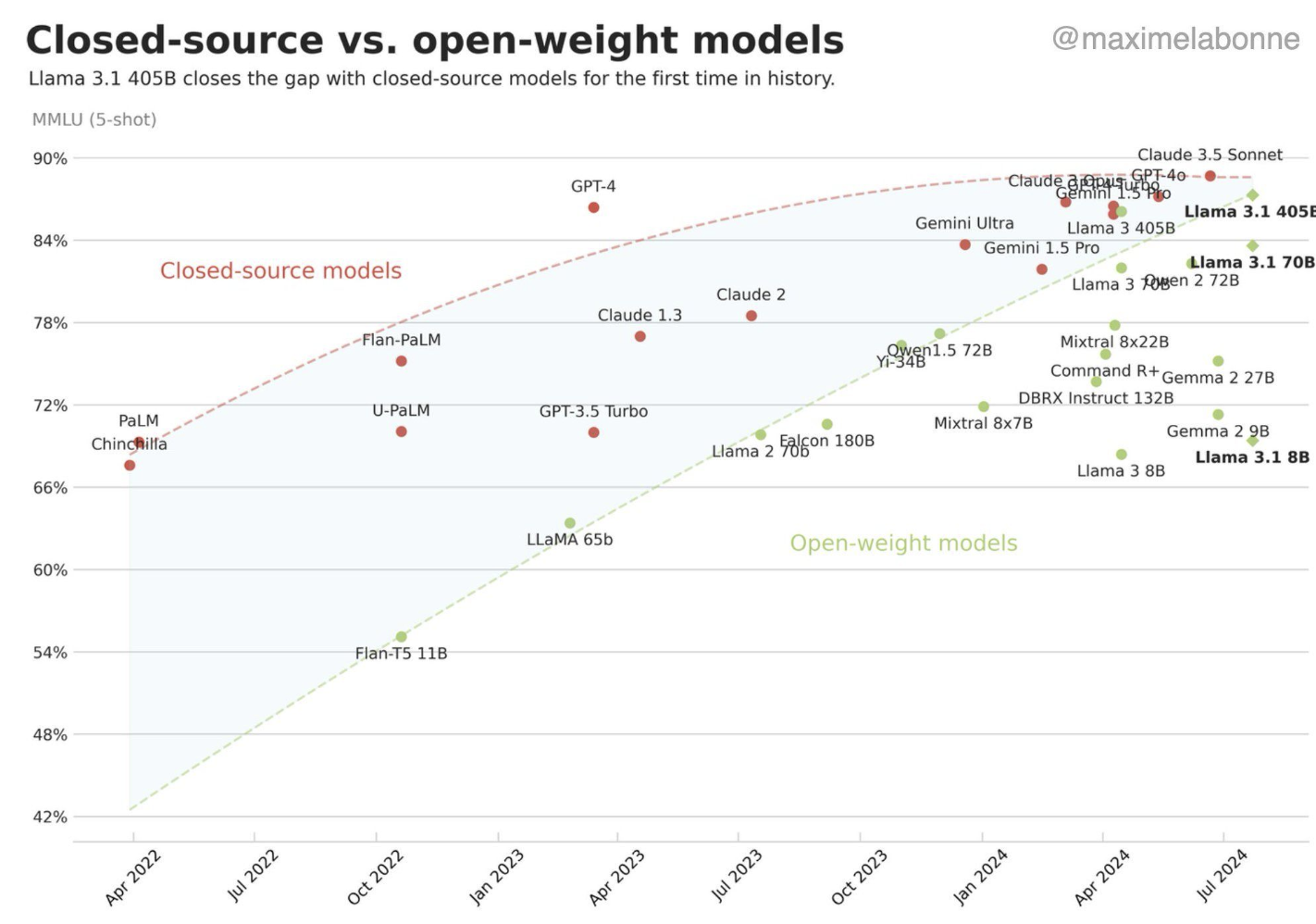
The following figure compares the maximum context length of the vanilla CoT without reduction (blue) and PENCIL with reduction (red). As problem complexity increases, PENCIL achieves dramatic space efficiency, notably reducing context length from 151,192 to just 3,335 tokens for Einstein’s Puzzle.

Maximal sequence length with and without the reduction rule.

Training and Experiments

The core difference between CoT and PENCIL during training is the calculation of the loss function:

For CoT, the loss for each new token is based on the complete historical context; for PENCIL, after each “write-erase” iteration, the model calculates loss for new tokens only on the reduced sequence. Although both generate the same number of tokens, PENCIL significantly shortens the context length corresponding to each token and thus is more efficient.

It’s also worthwhile to note that after each reduction, the KV cache for the shared prefix C can be directly reused, with only the cache for the shorter part A needing recalculation.

Experimental Results

Our experiments focus on three inherently hard reasoning tasks: 3-SAT (NP-Complete), QBF (PSPACE-Complete), and Einstein’s Puzzle (natural language reasoning). For each task, we wrote a generator to generate a training set where special tokens are included. We train a small transformer (SAT/QBF with 10.6M parameters; Einstein’s Puzzle with 25.2M parameters) starting with random initialization for these tasks.