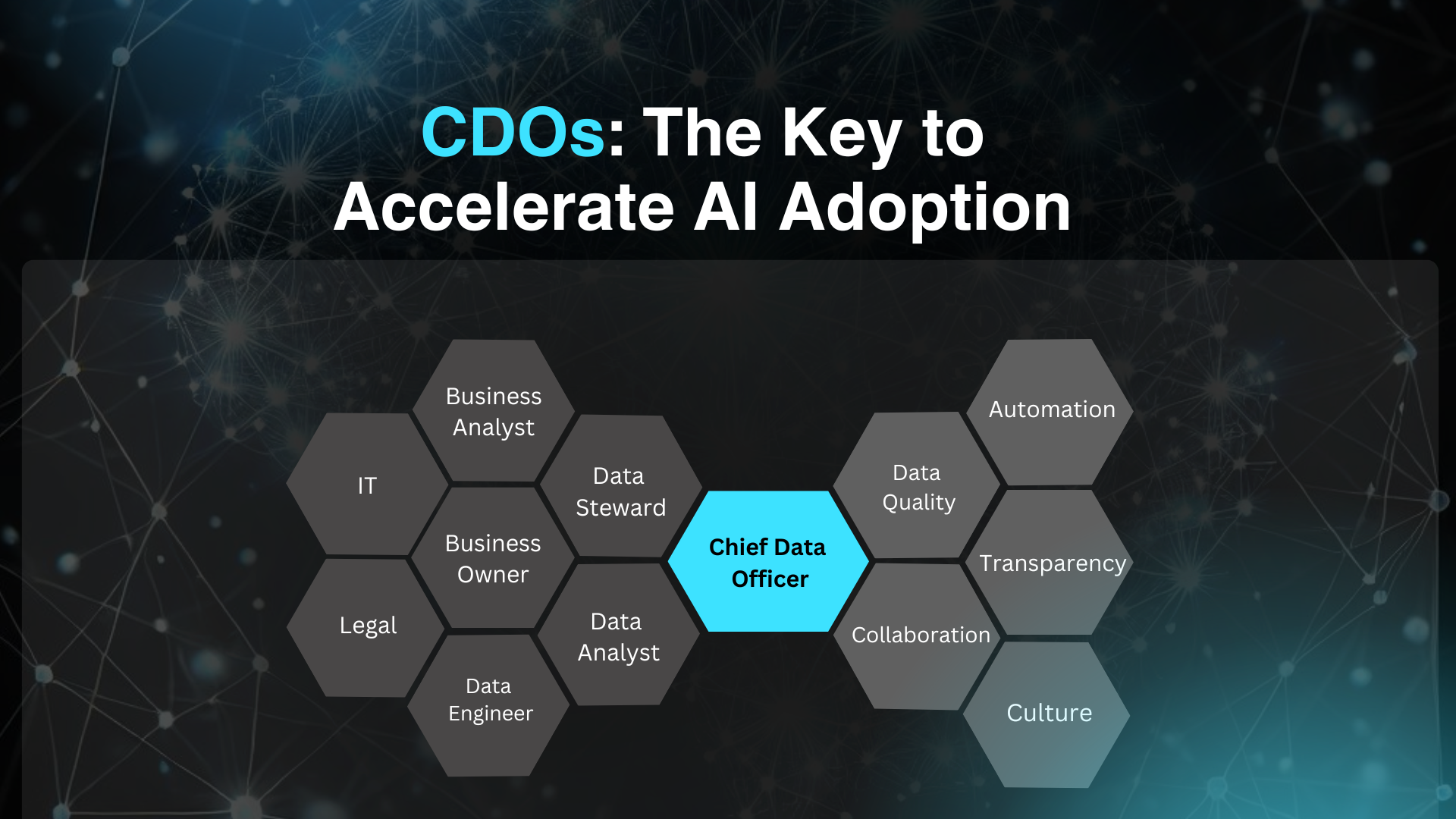
Determine Fundamental Constants with LEDs and a Multimeter
There are (probably) less than two dozen fundemental constants that define the physics of our universe. Determining the value of them might seem like the sort of thing for large, …read more


There are (probably) less than two dozen fundemental constants that define the physics of our universe. Determining the value of them might seem like the sort of thing for large, well funded University labs, but many can be determined to reasonable accuracy on the benchtop, as [Marb’s Lab] proves with this experiment to find the value of Planck’s Constant.
[Marv’s Lab] setup is on a nice PCB that uses a rotary switch to select between 5 LEDs of different wavelengths, with banana plugs for the multi-meter so he can perform a linear regression on the relation between energy and frequency to find the constant. He’s also thoughtfully put connectors in place for current measurement, so the volt-current relationship of the LEDs can be characterized in a second experiment. Overall, this is a piece of kit that would not be out of place in any high school or undergraduate physics lab.
To use this to determine Planck’s constant, you need to use Planck’s relation for the energy of a photon:
E = hf
Get some Energies (E), get some energies (f), and bam! You can generate a value for h, Planck’s constant. The energies? Well, that’s a very easy measurement, but it requires some understanding of how LEDs work. [Marb] is simply measuring the voltage needed to just barely light the LED of a given frequency. (For frequency, he’s relying on the LED datasheets.) That translates to the energy of the photon because it corresponds to the energy (in electron volts) required to jump electrons over the bandgap of the semiconductor in the LED– that’s how the light is generated. Those photons will have the energy of the gap, in theory.
In practice, the LEDs do not emit perfectly monochromatic light; there’s a normal distribution centered on the color they’re “supposed” to be, but it is fairly tight. That’s probably why is able to [Marv] get to within 5% of the canonical value, which is better than we’d expect.
This isn’t the first time we’ve determined plank’s constant; it’s quite possible to get to much higher accuracy. The last time we featured this particular technique, the error was 11%.






































































































































































![[The AI Show Episode 146]: Rise of “AI-First” Companies, AI Job Disruption, GPT-4o Update Gets Rolled Back, How Big Consulting Firms Use AI, and Meta AI App](https://www.marketingaiinstitute.com/hubfs/ep%20146%20cover.png)























































































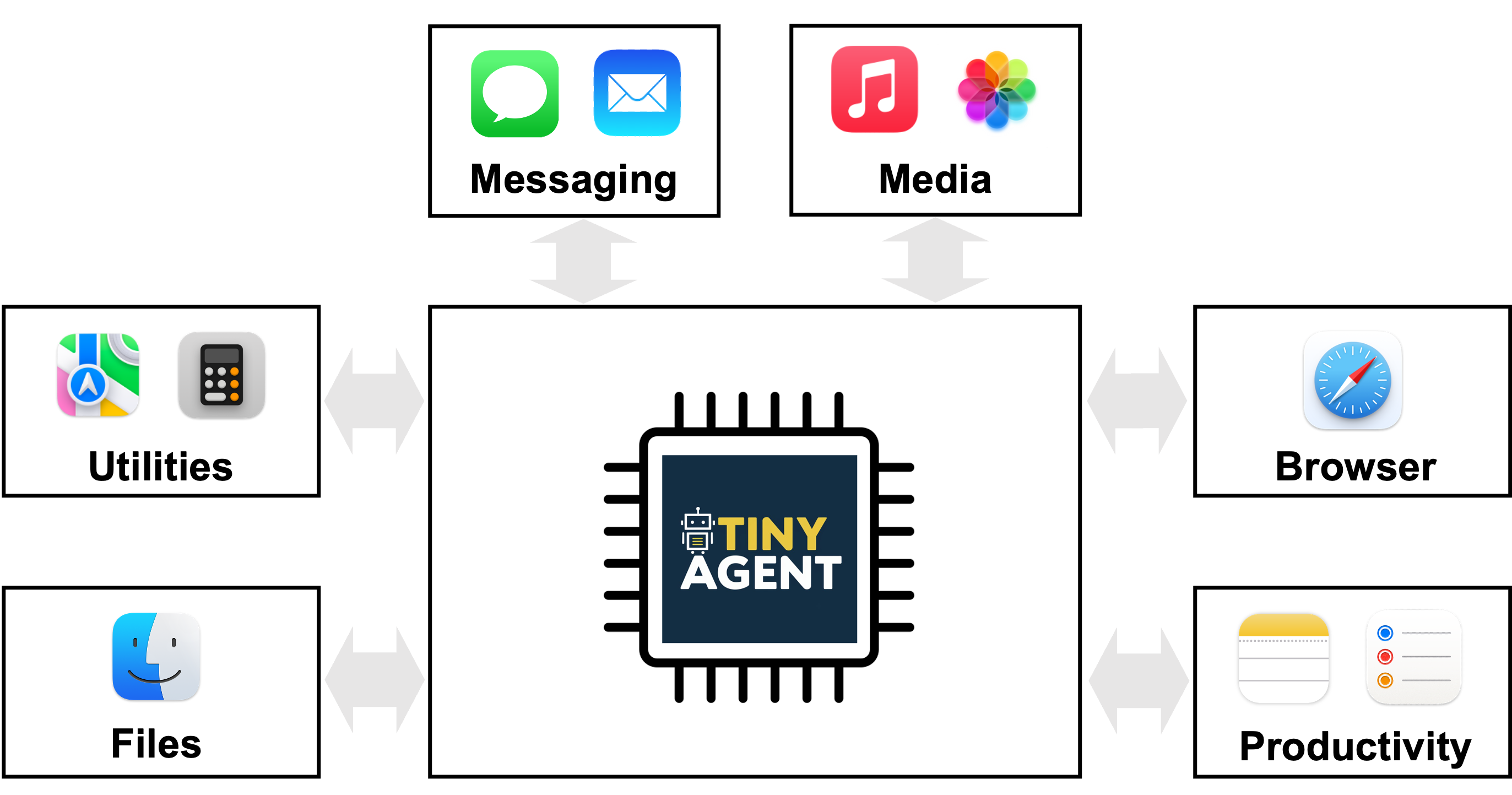
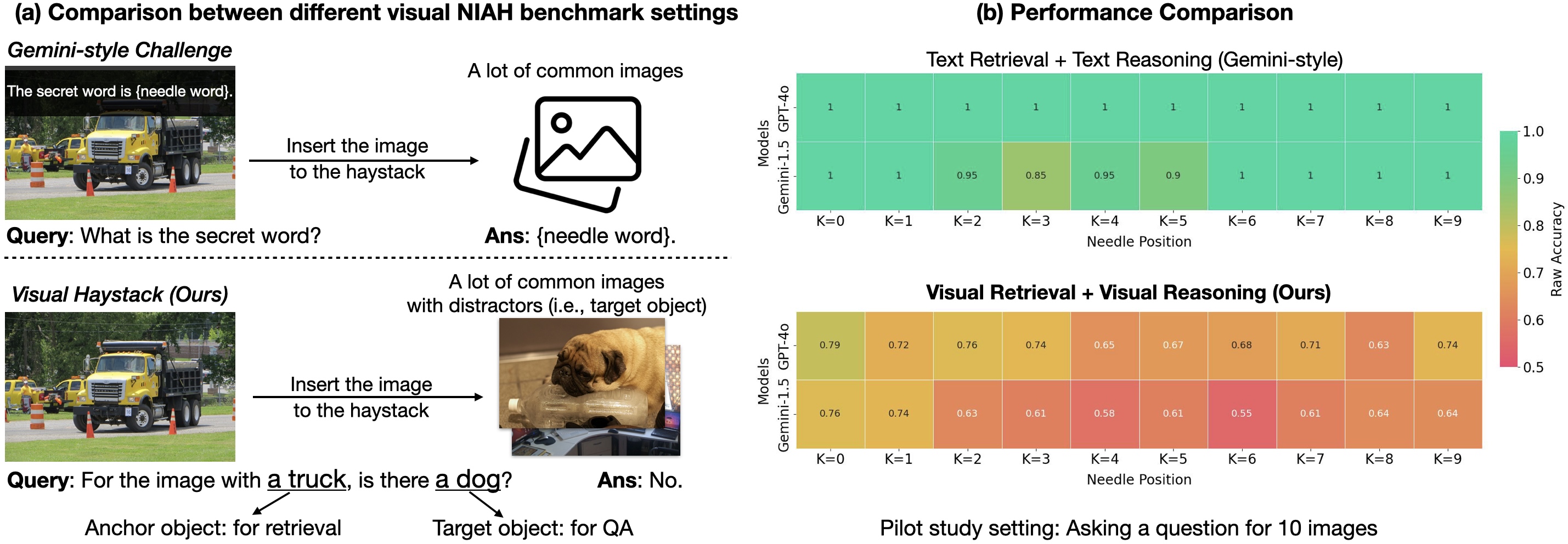



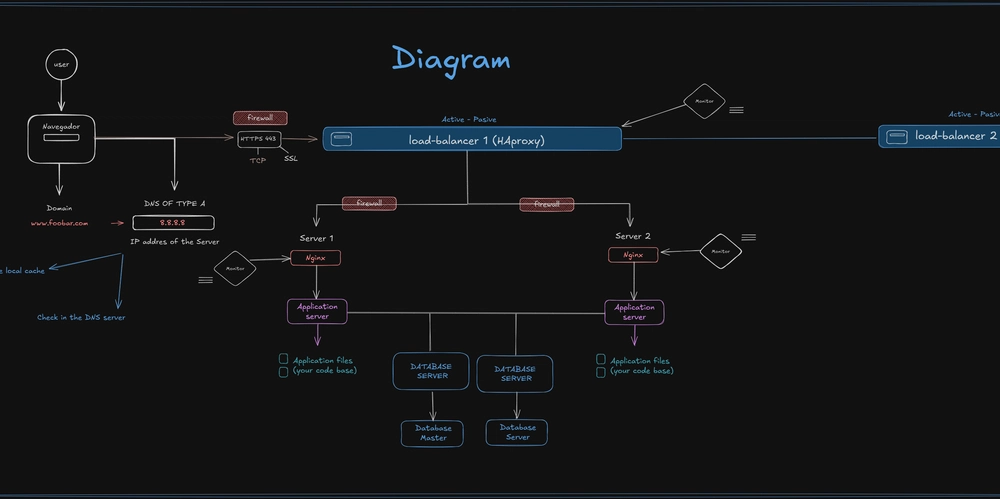



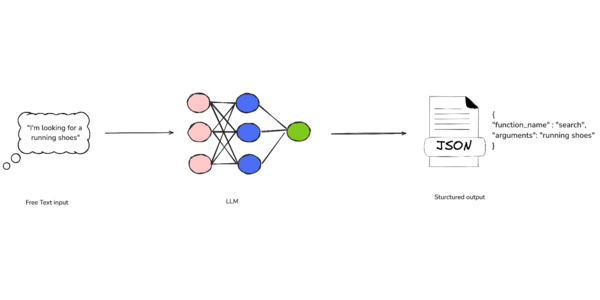




![[FREE EBOOKS] Modern Generative AI with ChatGPT and OpenAI Models, Offensive Security Using Python & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)




![How to make Developer Friends When You Don't Live in Silicon Valley, with Iraqi Engineer Code;Life [Podcast #172]](https://cdn.hashnode.com/res/hashnode/image/upload/v1747360508340/f07040cd-3eeb-443c-b4fb-370f6a4a14da.png?#)
































































































































![[Virtual Event] Strategic Security for the Modern Enterprise](https://eu-images.contentstack.com/v3/assets/blt6d90778a997de1cd/blt55e4e7e277520090/653a745a0e92cc040a3e9d7e/Dark_Reading_Logo_VirtualEvent_4C.png?width=1280&auto=webp&quality=80&disable=upscale#)












































































-xl-(1)-xl-xl.jpg)























![iPhone 17 Air Could Get a Boost From TDK's New Silicon Battery Tech [Report]](https://www.iclarified.com/images/news/97344/97344/97344-640.jpg)
![Vision Pro Owners Say They Regret $3,500 Purchase [WSJ]](https://www.iclarified.com/images/news/97347/97347/97347-640.jpg)
![Apple Showcases 'Magnifier on Mac' and 'Music Haptics' Accessibility Features [Video]](https://www.iclarified.com/images/news/97343/97343/97343-640.jpg)
![Sony WH-1000XM6 Unveiled With Smarter Noise Canceling and Studio-Tuned Sound [Video]](https://www.iclarified.com/images/news/97341/97341/97341-640.jpg)