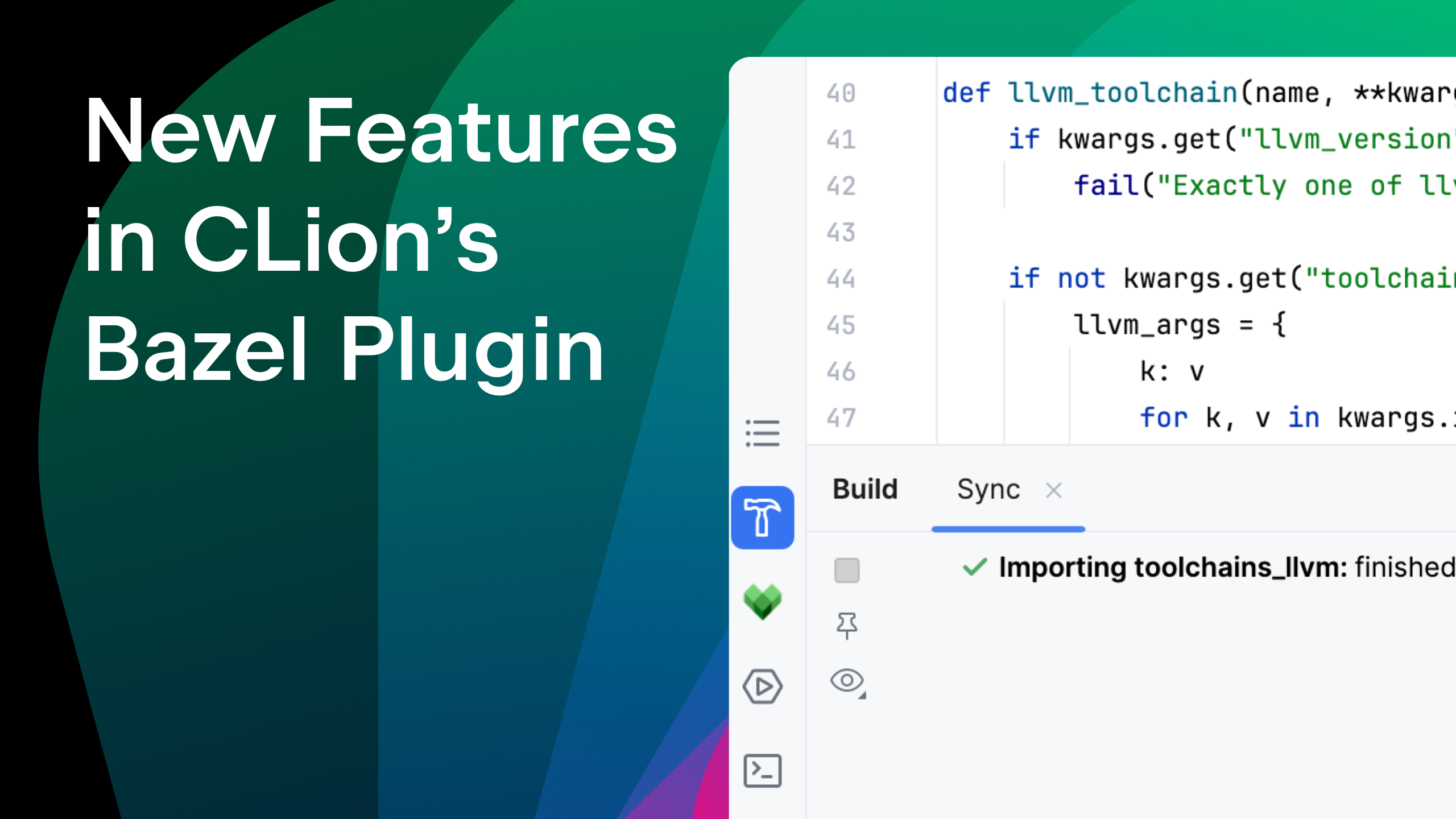
Deep attractors: Where deep learning meets chaos
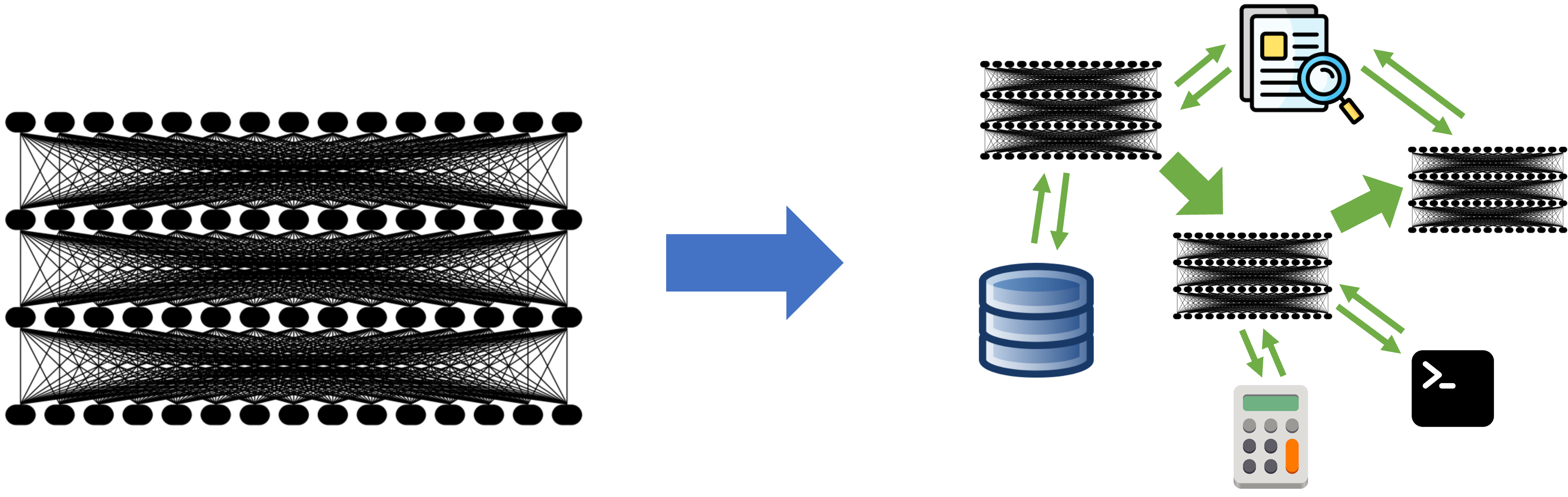
In nonlinear dynamics, when the state space is thought to be multidimensional but all we have for data is just a univariate time series, one may attempt to reconstruct the true space via delay coordinate embeddings. However, it is not clear a priori how to choose dimensionality and time lag of the reconstruction space. In this post, we show how to use an autoencoder architecture to circumvent the problem: Given just a scalar series of observations, the autoencoder directly learns to represent attractors of chaotic systems in adequate dimensionality.
In nonlinear dynamics, when the state space is thought to be multidimensional but all we have for data is just a univariate time series, one may attempt to reconstruct the true space via delay coordinate embeddings. However, it is not clear a priori how to choose dimensionality and time lag of the reconstruction space. In this post, we show how to use an autoencoder architecture to circumvent the problem: Given just a scalar series of observations, the autoencoder directly learns to represent attractors of chaotic systems in adequate dimensionality.












































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)


























































































































![[DEALS] Microsoft Office Professional 2021 for Windows: Lifetime License (75% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)







































































































































_Anthony_Brown_Alamy.jpg?#)
_Hanna_Kuprevich_Alamy.jpg?#)




.png?#)




















































































![Hands-on: We got to play Nintendo Switch 2 for nearly six hours yesterday [Video]](https://i0.wp.com/9to5toys.com/wp-content/uploads/sites/5/2025/04/Switch-FI-.jpg.jpg?resize=1200%2C628&ssl=1)
![Fitbit redesigns Water stats and logging on Android, iOS [U]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2023/03/fitbit-logo-2.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)














![YouTube Announces New Creation Tools for Shorts [Video]](https://www.iclarified.com/images/news/96923/96923/96923-640.jpg)

![Apple Faces New Tariffs but Has Options to Soften the Blow [Kuo]](https://www.iclarified.com/images/news/96921/96921/96921-640.jpg)