Counting Sort
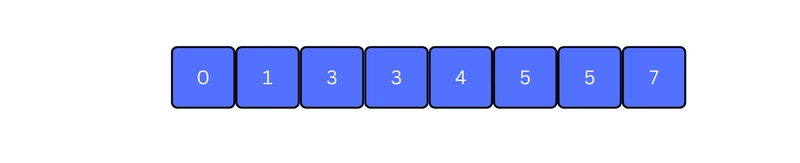
Counting Sort is a sorting method that works by: 1. Counting how many times each number appears in the list. 2. Using those counts to figure out where each number should go in the final sorted list. It uses an extra array to keep track of how many times each number appears, and then builds the sorted list based on those counts. Working of Counting Sort 1. Find out the maximum element (let it be max) from the given array. 2. Create a new array of size max + 1, and set all its elements to 0. This array will be used to store how many times each number appears in the original array. 3. Store the count of each element at their respective index in count array. For example: if the count of element 3 is 2 then, 2 is stored in the 3rd index of count array. If element "5" is not present in the array, then 0 is stored in 5th index. 4. Change the count array so that each position stores the total of all previous counts. This helps us know the correct position of each number in the sorted array. 5. For each element in the original array, find its value in the count array — this gives its position in the sorted array. Place the element at that position. Then, decrease the count by one. You can see this clearly in the iteration steps below: 6. Final sorted array is : Counting Sort Algorithm countingSort(array, size) max
Counting Sort is a sorting method that works by:
1. Counting how many times each number appears in the list.
2. Using those counts to figure out where each number should go in the final sorted list.
It uses an extra array to keep track of how many times each number appears, and then builds the sorted list based on those counts.
Working of Counting Sort
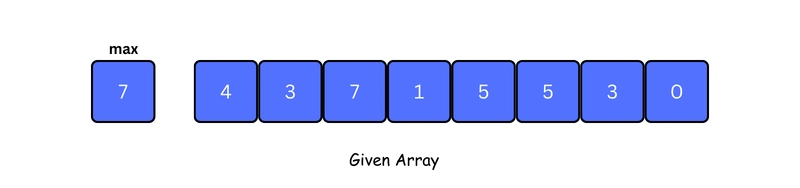
1. Find out the maximum element (let it be max) from the given array.
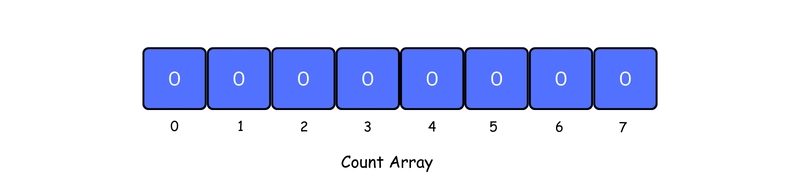
2. Create a new array of size max + 1, and set all its elements to 0. This array will be used to store how many times each number appears in the original array.
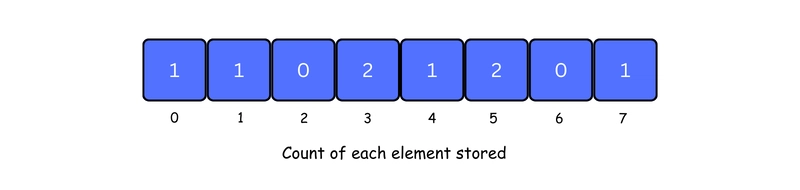
3. Store the count of each element at their respective index in count array.
For example: if the count of element 3 is 2 then, 2 is stored in the 3rd index of count array. If element "5" is not present in the array, then 0 is stored in 5th index.
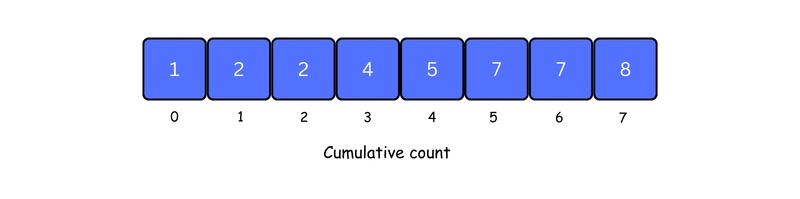
4. Change the count array so that each position stores the total of all previous counts. This helps us know the correct position of each number in the sorted array.
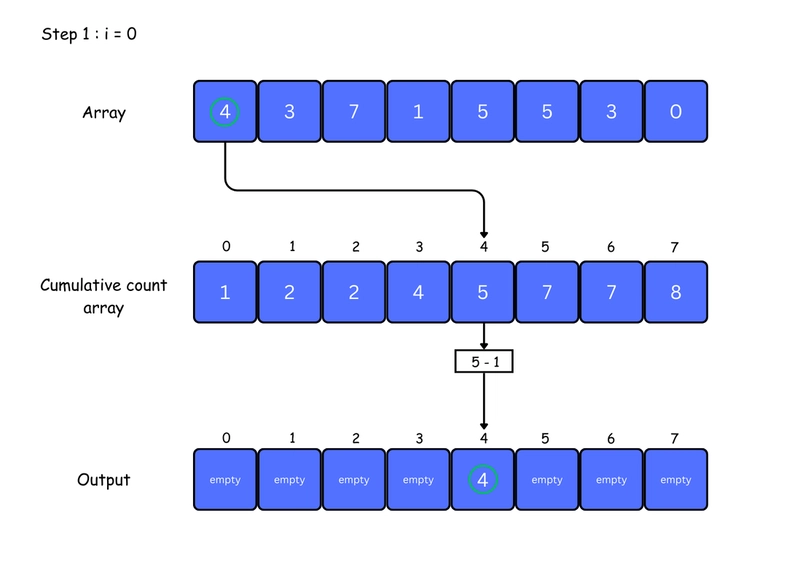
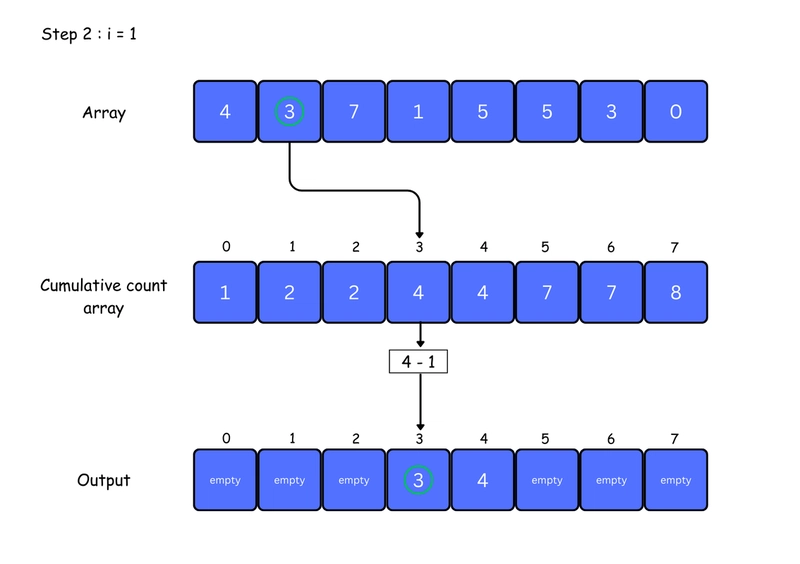
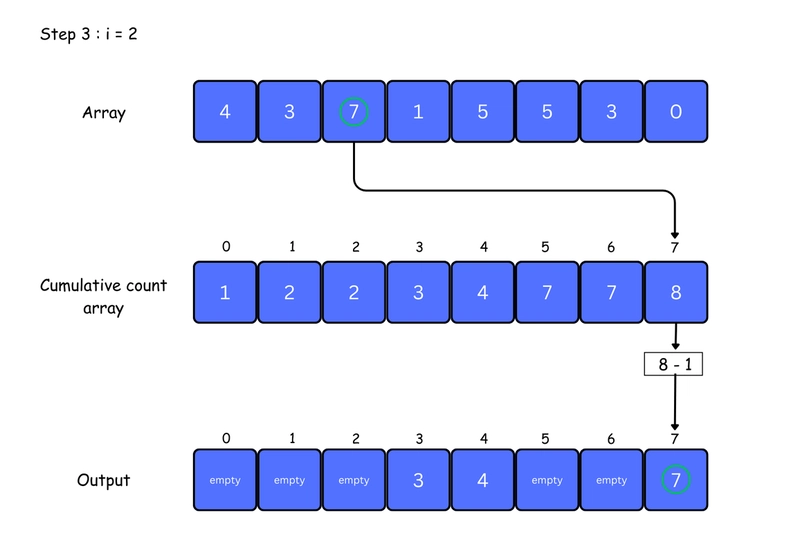
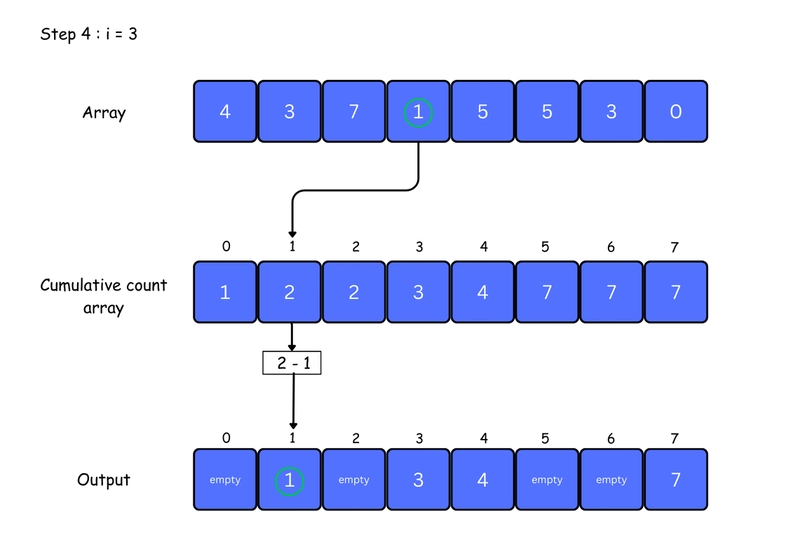
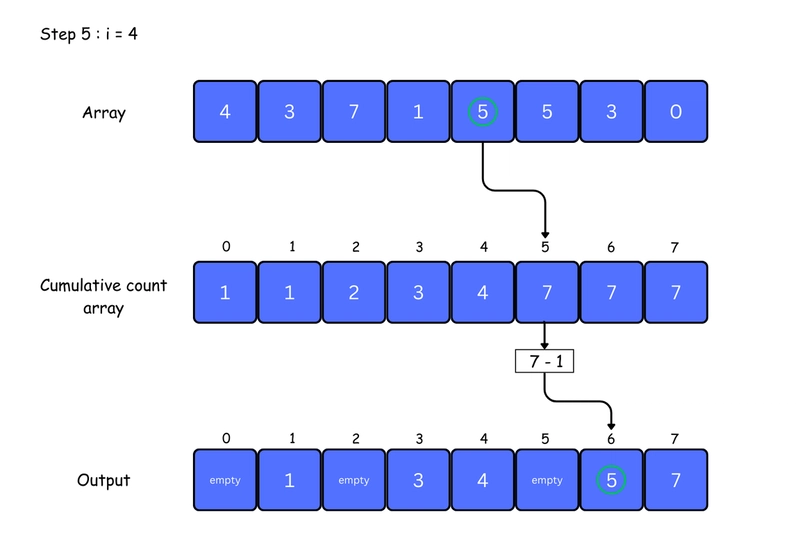
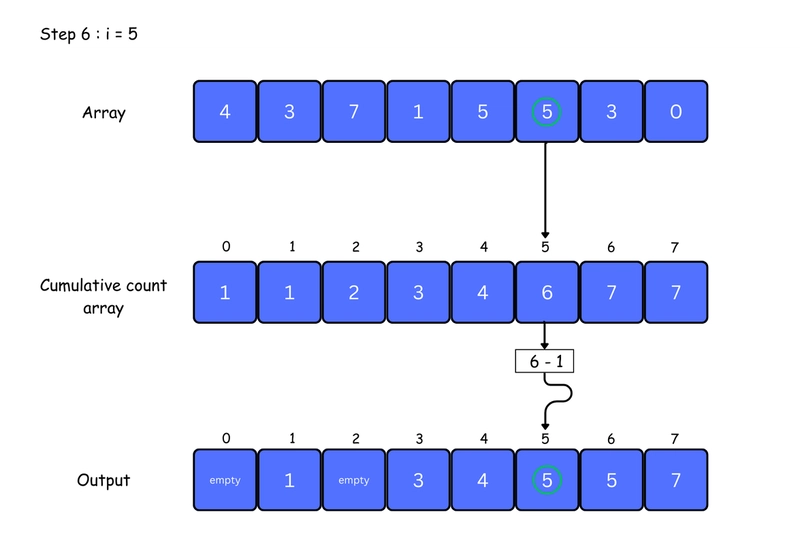
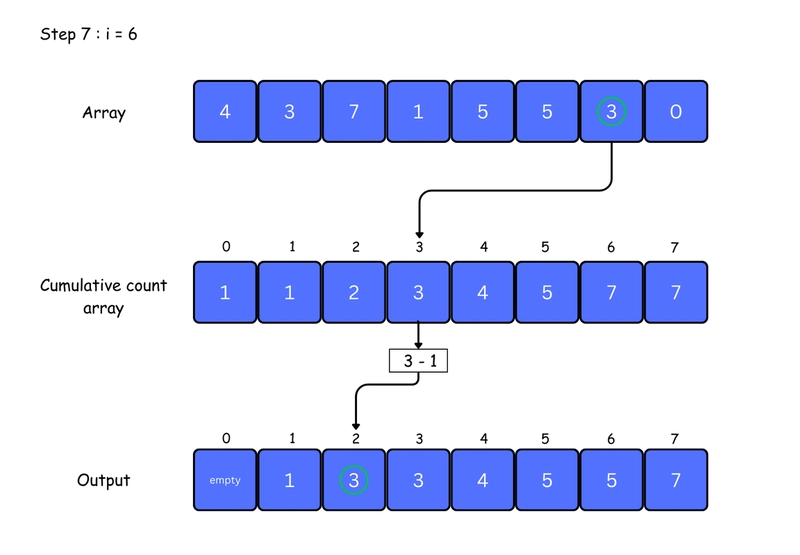
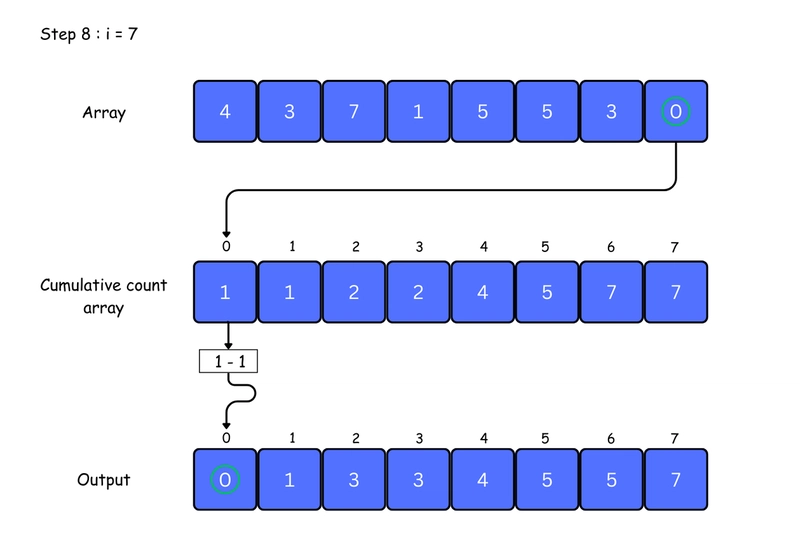
5. For each element in the original array, find its value in the count array — this gives its position in the sorted array. Place the element at that position. Then, decrease the count by one. You can see this clearly in the iteration steps below:
Counting Sort Algorithm
countingSort(array, size)
max <- find largest element in array
initialize count array with all zeros
for j <- 0 to size
find the total count of each unique element and
store the count at jth index in count array
for i <- 1 to max
find the cumulative sum and store it in count array itself
for j <- size down to 1
restore the elements to array
decrease count of each element restored by 1
Counting Sort Code
function countingSort(arr) {
let n = arr.length;
//finding the max element in the array
let max = 0;
for (let i = 0; i < n; i++) {
max = Math.max(arr[i], max);
}
//creating a count array of size max+1
let countArray = new Array(max + 1).fill(0);
// storing the frequency of each element in the count array
for (let i = 0; i < n; i++) {
countArray[arr[i]]++;
}
// storing the cumulative frequency of each element in the count array
for (let i = 1; i < countArray.length; i++) {
countArray[i] += countArray[i - 1];
}
let output = new Array(n);
// creating outputArray from countArray
for (let i = 0; i < n; i++) {
output[countArray[arr[i]] - 1] = arr[i];
countArray[arr[i]]--;
}
return output;
}
const inputArray = [4, 3, 12, 1, 5, 5, 3, 9];
console.log(countingSort(inputArray));
Merge Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(n+max) |
| Worst | O(n+max) |
| Average | O(n+max) |
| Space Complexity | O(max) |
| Stability | Yes |
1. Time Complexities
Worst Case Complexity: O(n+max)
Best Case Complexity: O(n+max)
Average Case Complexity: O(n+max)
2. Space Complexity
- Space Complexity: O(max) The space complexity of Counting Sort is O(max). Larger the range of elements, larger is the space complexity.
Applications of Counting Sort:
1. Sorting Student Scores / Grades
- If you have a list of students' scores (e.g., 0–100), Counting Sort can sort them super quickly.
2. Sorting Ages in a Survey
- If you’re dealing with ages (say, 1–120), Counting Sort is very efficient since the range is limited.
3. Sorting Colors (like in graphics or games)
- When colors are represented by integer codes (like 0 = red, 1 = green, 2 = blue).
4. Sorting Characters in Strings (if we consider ASCII values)
- You can sort characters in a string in O(n) time since there are only 256 possible ASCII values (or 26 for lowercase a–z).
5. In Radix Sort as a sub-routine
- Counting Sort is often used within Radix Sort to sort digits efficiently because it preserves the order of equivalent elements (it's stable).
6. Sorting Event Timestamps (if timestamps are integers within a known range)
- Can be used for sorting logs, or event times if the time is discretized to seconds, milliseconds, etc.

















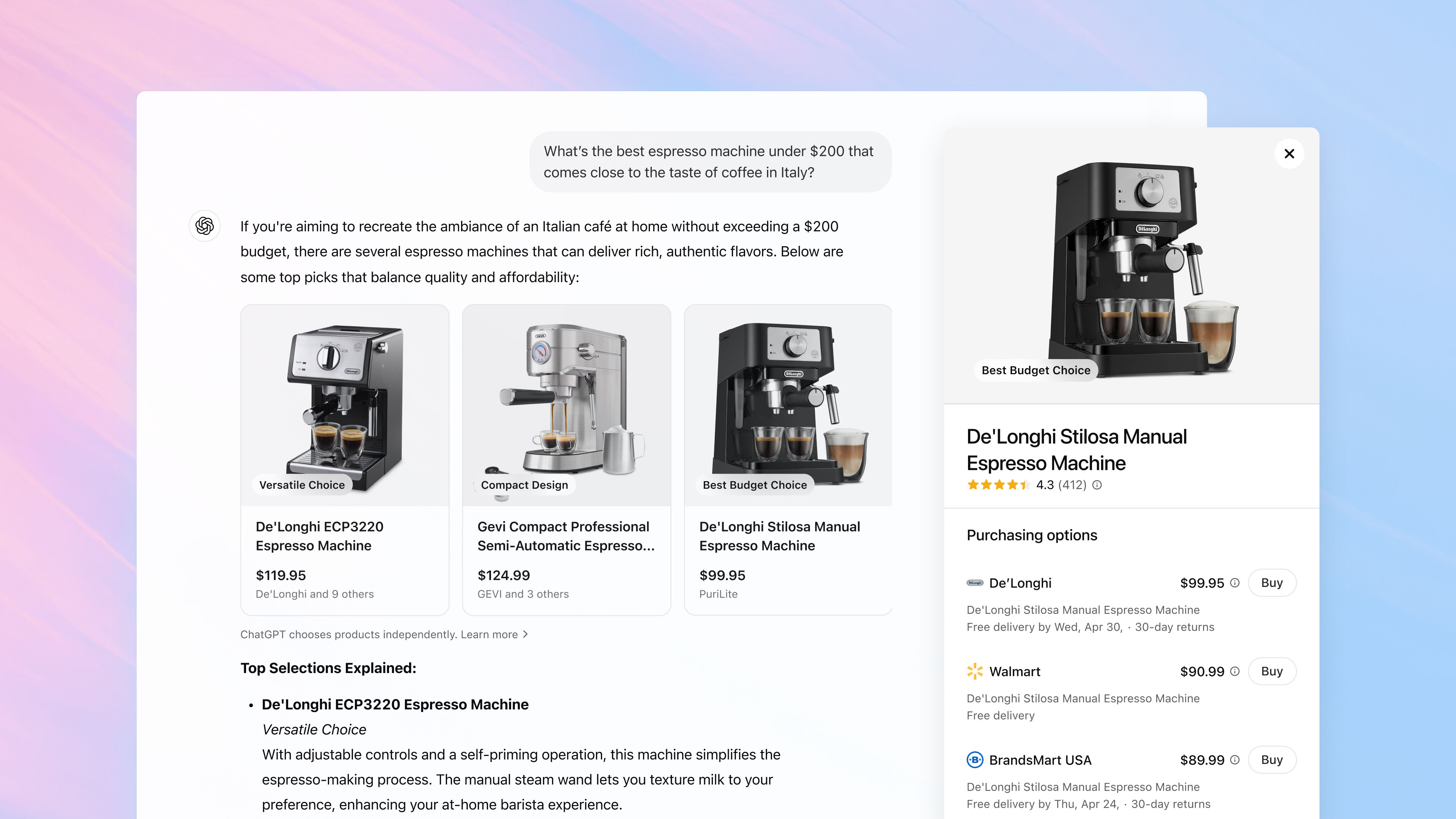














































































































































![[The AI Show Episode 145]: OpenAI Releases o3 and o4-mini, AI Is Causing “Quiet Layoffs,” Executive Order on Youth AI Education & GPT-4o’s Controversial Update](https://www.marketingaiinstitute.com/hubfs/ep%20145%20cover.png)


![[The AI Show Episode 143]: ChatGPT Revenue Surge, New AGI Timelines, Amazon’s AI Agent, Claude for Education, Model Context Protocol & LLMs Pass the Turing Test](https://www.marketingaiinstitute.com/hubfs/ep%20143%20cover.png)















































































































































































































































.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)
.png?width=1920&height=1920&fit=bounds&quality=70&format=jpg&auto=webp#)























_Muhammad_R._Fakhrurrozi_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)








































































































![AirPods Pro 2 With USB-C Back On Sale for Just $169! [Deal]](https://www.iclarified.com/images/news/96315/96315/96315-640.jpg)
![Apple Releases iOS 18.5 Beta 4 and iPadOS 18.5 Beta 4 [Download]](https://www.iclarified.com/images/news/97145/97145/97145-640.jpg)
![Apple Seeds watchOS 11.5 Beta 4 to Developers [Download]](https://www.iclarified.com/images/news/97147/97147/97147-640.jpg)
![Apple Seeds visionOS 2.5 Beta 4 to Developers [Download]](https://www.iclarified.com/images/news/97150/97150/97150-640.jpg)