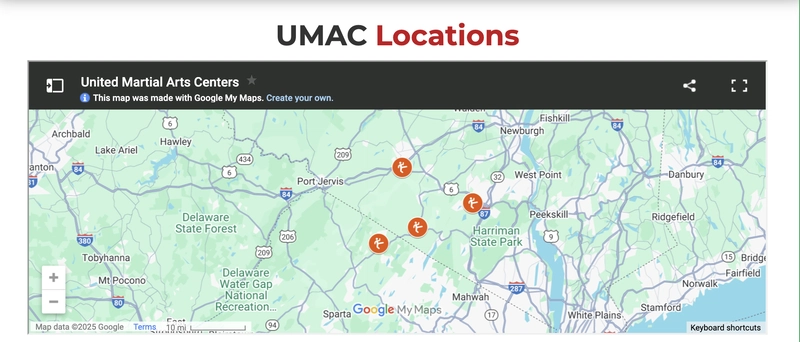
Sorting Algorithm: Selection

Selection sort makes sure that it selects the smallest (or largest, depending on the implementation) element from the unsorted portion of the array and moves it to its correct position from the start of the array. SelectionSort(arr, n): for i from 0 to n-2: // i loops over each element except the last minElemIdx = i // let first element of the unsorted part is the smallest for j from i+1 to n-1: // j loops through out the unsorted part, to get minimum value index of this part if arr[j] < arr[minElemIdx]: minElemIdx = j Swap arr[i] and arr[minElemIdx] // smallest element at its correct position lets take an example array to do dry-run for selection sort(ascending order): array has values -2, 4, -6, -5, 1 so array after selection sort, would be -6, -5, -2, 1, 4 1st outer loop i = 0 minElemIdx = i = 0 1st inner loop j = i + 1 -> 0 + 1 -> 1 4 < -2 (false) j = 2 -6 < -2 (true) minElemIdx = 2 j = 3 -5 < -6 (false) j = 4 1 < -6 (false) 1st inner loop completed Swap -2 (arr[0]) and -6(arr[minElemIdx]) -6 4 -2 -5 1 1st outer loop completed If you observe here, our first element is the least element in the array Now on to the second 2nd outer loop i = 1 minElemIdx = i = 1 2nd inner loop j = i + 1 = 2 -2 < 4 (true) minElemIdx = 2 j = 3 -5 < -2 (true) minElemIdx = 3 j = 4 4 < 1 (false) 2nd inner loop completed Swap 4 (arr[1]) and -6 (arr[minElemIdx]) -6 -5 -2 4 1 2nd outer loop completed 3rd outer loop i = 2 minElemIdx = i = 2 3rd inner loop j = i + 1 = 3 4 < -2 (false) j = 4 1 < -2 (false) 3rd inner loop completed Swap won't happen as minElemIdx is same as i -6 -5 -2 4 1 3rd outer loop completed 4th outer loop i = 3 minElemidx = i = 3 4th inner loop j = i + 1 = 4 1 < 4 (true) minElemIdx = 4 4th inner loop completed Swap 4(arr[3]) and 1(arr[minElemIdx]) -6 -5 -2 1 4 4th outer loop completed We reached the sorted output using selection sort algorithm This is one of the many in-place sorting algorithms with space complexity is O(1)(i.e.) it doesn't need an extra space to perform this. This takes less memory writes during the sorting algorithm(next to cycle sort) Flip side or a major drawback with this sorting algorithm is that the time complexity is O(n^2) (Inner loop O(n) * Outer loop O(n))

Mar 13, 2025 - 19:02

Selection sort makes sure that it selects the smallest (or largest, depending on the implementation) element from the unsorted portion of the array and moves it to its correct position from the start of the array.

SelectionSort(arr, n):
    for i from 0 to n-2:    // i loops over each element except the last
        minElemIdx = i       // let first element of the unsorted part is the smallest
        for j from i+1 to n-1:  // j loops through out the unsorted part, to get minimum value index of this part
            if arr[j] < arr[minElemIdx]: 
                minElemIdx = j
        Swap arr[i] and arr[minElemIdx]  // smallest element at its correct position

lets take an example array to do dry-run for selection sort(ascending order):

array has values -2, 4, -6, -5, 1
so array after selection sort, would be -6, -5, -2, 1, 4

1st outer loop
i = 0
minElemIdx = i = 0

1st inner loop
j = i + 1 -> 0 + 1 -> 1
4 < -2 (false)
j = 2
-6 < -2 (true)
minElemIdx = 2
j = 3
-5 < -6 (false)
j = 4
1 < -6 (false)
1st inner loop completed

Swap -2 (arr[0]) and -6(arr[minElemIdx])

-6 4 -2 -5 1
1st outer loop completed

If you observe here, our first element is the least element in the array
Now on to the second

2nd outer loop
i = 1
minElemIdx = i = 1

2nd inner loop
j = i + 1 = 2
-2 < 4 (true)
minElemIdx = 2
j = 3
-5 < -2 (true)
minElemIdx = 3
j = 4
4 < 1 (false)
2nd inner loop completed

Swap 4 (arr[1]) and -6 (arr[minElemIdx])

-6 -5 -2 4 1
2nd outer loop completed

3rd outer loop
i = 2
minElemIdx = i = 2

3rd inner loop
j = i + 1 = 3
4 < -2 (false)
j = 4
1 < -2 (false)
3rd inner loop completed

Swap won't happen as minElemIdx is same as i

-6 -5 -2 4 1
3rd outer loop completed

4th outer loop
i = 3
minElemidx = i = 3

4th inner loop
j = i + 1 = 4
1 < 4 (true)
minElemIdx = 4
4th inner loop completed

Swap 4(arr[3]) and 1(arr[minElemIdx])

-6 -5 -2 1 4
4th outer loop completed

We reached the sorted output using selection sort algorithm

This is one of the many in-place sorting algorithms with space complexity is O(1)(i.e.) it doesn't need an extra space to perform this. This takes less memory writes during the sorting algorithm(next to cycle sort)

Flip side or a major drawback with this sorting algorithm is that the time complexity is O(n^2) (Inner loop O(n) * Outer loop O(n))