Leetcode 621. Task Scheduler

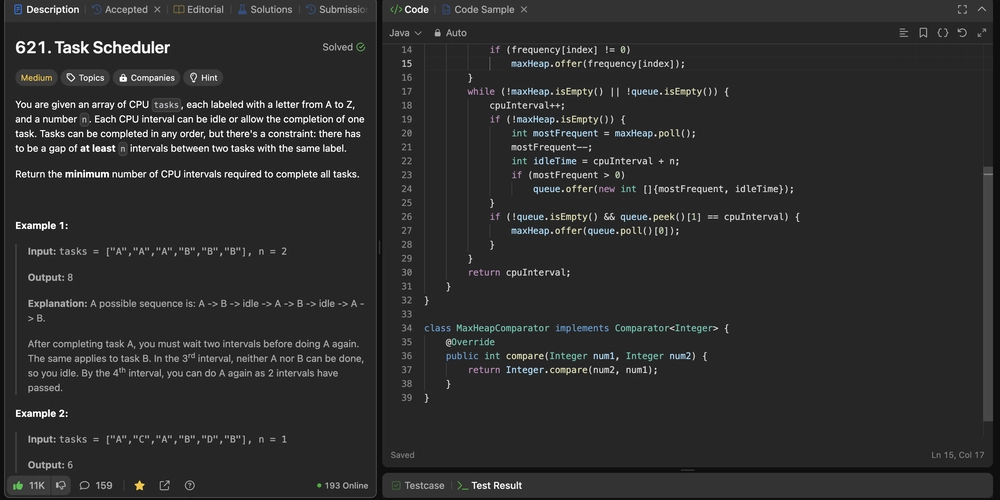
Problem You are given an array of CPU tasks, each labeled with a letter from A to Z, and a number n. Each CPU interval can be idle or allow the completion of one task. Tasks can be completed in any order, but there's a constraint: there has to be a gap of at least n intervals between two tasks with the same label. Return the minimum number of CPU intervals required to complete all tasks. Sample Input Example 1: Input: tasks = ["A","A","A","B","B","B"], n = 2 Output: 8 Explanation: A possible sequence is: A -> B -> idle -> A -> B -> idle -> A -> B. After completing task A, you must wait two intervals before doing A again. The same applies to task B. In the 3rd interval, neither A nor B can be done, so you idle. By the 4th interval, you can do A again as 2 intervals have passed. Example 2: Input: tasks = ["A","C","A","B","D","B"], n = 1 Output: 6 Explanation: A possible sequence is: A -> B -> C -> D -> A -> B. With a cooling interval of 1, you can repeat a task after just one other task. Example 3: Input: tasks = ["A","A","A", "B","B","B"], n = 3 Output: 10 Explanation: A possible sequence is: A -> B -> idle -> idle -> A -> B -> idle -> idle -> A -> B. There are only two types of tasks, A and B, which need to be separated by 3 intervals. This leads to idling twice between repetitions of these tasks. Constraints 1

Mar 30, 2025 - 18:17

Problem

You are given an array of CPU tasks, each labeled with a letter from A to Z, and a number n. Each CPU interval can be idle or allow the completion of one task. Tasks can be completed in any order, but there's a constraint: there has to be a gap of at least n intervals between two tasks with the same label.

Return the minimum number of CPU intervals required to complete all tasks.

Sample Input

Example 1:

Input: tasks = ["A","A","A","B","B","B"], n = 2

Output: 8

Explanation: A possible sequence is: A -> B -> idle -> A -> B -> idle -> A -> B.

After completing task A, you must wait two intervals before doing A again. The same applies to task B. In the 3rd interval, neither A nor B can be done, so you idle. By the 4th interval, you can do A again as 2 intervals have passed.

Example 2:

Input: tasks = ["A","C","A","B","D","B"], n = 1

Output: 6

Explanation: A possible sequence is: A -> B -> C -> D -> A -> B.

With a cooling interval of 1, you can repeat a task after just one other task.

Example 3:

Input: tasks = ["A","A","A", "B","B","B"], n = 3

Output: 10

Explanation: A possible sequence is: A -> B -> idle -> idle -> A -> B -> idle -> idle -> A -> B.

There are only two types of tasks, A and B, which need to be separated by 3 intervals. This leads to idling twice between repetitions of these tasks.

Constraints

1 <= tasks.length <= 10^4
tasks[i] is an uppercase English letter.
0 <= n <= 100

Intuition

Suppose we start scheduling the less frequent task, then the idle time would be more for the more frequent tasks.
AAABBCC and idle time = 1 -> If we start from, say C, then one possible way could have been
CBCBA_A_A = 9 total CPU intervals, which is high.
Thus, we can try to have more frequent tasks to be done every time. To know the most frequent task after processing every task, a max heap can be used.

Approach

Store the frequency of the characters in an array or map.
Move all the frequencies that are non-zero to the max heap.
Initialise a queue with new elements as [frequency, idleTime], which can be used to push back the task to the maxHeap once the idleTime of the particular task is over.
Repeat the process until both the maxHeap and the queue are empty.

Complexity

Time complexity:
O(N) + O(26) + O(26log26)
Space complexity:
O(26)

Code

class Solution {
    public int leastInterval(char[] tasks, int n) {
        if (tasks == null || tasks.length == 0) {
            return 0;
        }
        int [] frequency = new int [26];
        for (char ch : tasks) {
            frequency[ch - 'A']++;
        }
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new MaxHeapComparator());
        Queue<int[]> queue = new LinkedList<>();
        int cpuInterval = 0;
        for (int index = 0; index < 26; index++) {
            if (frequency[index] != 0)
                maxHeap.offer(frequency[index]);
        }
        while (!maxHeap.isEmpty() || !queue.isEmpty()) {
            cpuInterval++;
            if (!maxHeap.isEmpty()) {
                int mostFrequent = maxHeap.poll();
                mostFrequent--;
                int idleTime = cpuInterval + n;
                if (mostFrequent > 0)
                    queue.offer(new int []{mostFrequent, idleTime});
            }
            if (!queue.isEmpty() && queue.peek()[1] == cpuInterval) {
                maxHeap.offer(queue.poll()[0]);
            }
        }
        return cpuInterval;
    }
}

class MaxHeapComparator implements Comparator<Integer> {
    @Override
    public int compare(Integer num1, Integer num2) {
        return Integer.compare(num2, num1);
    }
}