2176. Count Equal and Divisible Pairs in an Array
2176. Count Equal and Divisible Pairs in an Array Difficulty: Easy Topics: Array Given a 0-indexed integer array nums of length n and an integer k, return the number of pairs (i, j) where 0
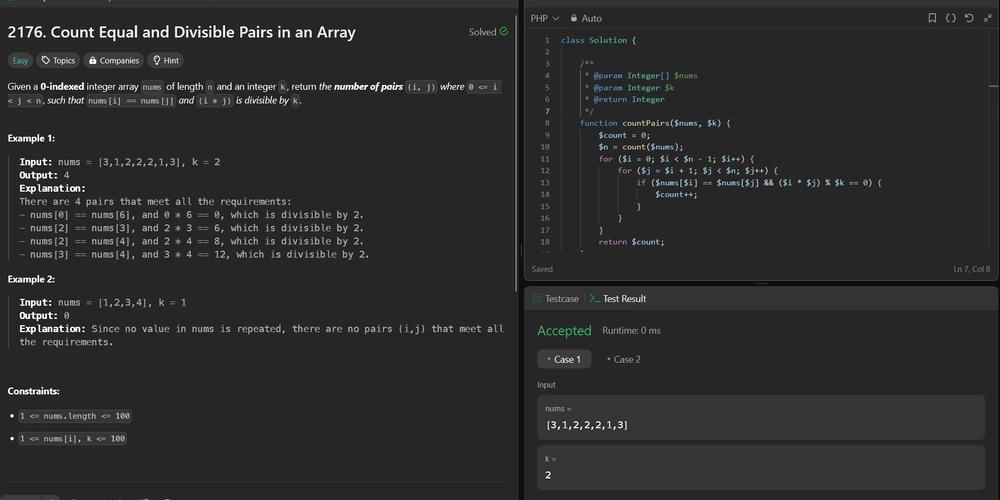
2176. Count Equal and Divisible Pairs in an Array
Difficulty: Easy
Topics: Array
Given a 0-indexed integer array nums of length n and an integer k, return the number of pairs (i, j) where 0 <= i < j < n, such that nums[i] == nums[j] and (i * j) is divisible by k.
Example 1:
- Input: nums = [3,1,2,2,2,1,3], k = 2
- Output: 4
-
Explanation: There are 4 pairs that meet all the requirements:
- nums[0] == nums[6], and 0 * 6 == 0, which is divisible by 2.
- nums[2] == nums[3], and 2 * 3 == 6, which is divisible by 2.
- nums[2] == nums[4], and 2 * 4 == 8, which is divisible by 2.
- nums[3] == nums[4], and 3 * 4 == 12, which is divisible by 2.
Example 2:
- Input: nums = [1,2,3,4], k = 1
- Output: 0
- Explanation: Since no value in nums is repeated, there are no pairs (i,j) that meet all the requirements.
Constraints:
1 <= nums.length <= 1001 <= nums[i], k <= 100
Hint:
- For every possible pair of indices (i, j) where i < j, check if it satisfies the given conditions.
Solution:
We need to count the number of pairs (i, j) in a given array such that the elements at these indices are equal and the product of their indices is divisible by a given integer k.
Approach
The approach involves iterating through all possible pairs of indices (i, j) where i < j. For each pair, we check two conditions:
- The elements at indices i and j are equal.
- The product of i and j is divisible by k.
Given the constraints that the array length is at most 100, a brute-force approach is feasible. This approach involves checking each pair directly, which is manageable due to the small size of the input.
Let's implement this solution in PHP: 2176. Count Equal and Divisible Pairs in an Array
/**
* @param Integer[] $nums
* @param Integer $k
* @return Integer
*/
function countPairs($nums, $k) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example 1:
$nums1 = array(3, 1, 2, 2, 2, 1, 3);
$k1 = 2;
echo "Output: " . countPairs($nums1, $k1) . "\n"; // Output: 4
// Example 2:
$nums2 = array(1, 2, 3, 4);
$k2 = 1;
echo "Output: " . countPairs($nums2, $k2) . "\n"; // Output: 0
?>
Explanation:
- Initialization: We start by initializing a counter to keep track of valid pairs.
- Nested Loops: We use two nested loops to generate all possible pairs (i, j) where i < j. The outer loop runs from 0 to n-2, and the inner loop runs from i+1 to n-1.
- Condition Check: For each pair (i, j), we check if the elements at these indices are equal and if their product modulo k is zero. If both conditions are met, we increment the counter.
- Return Result: Finally, we return the count of valid pairs.
This approach ensures that we check all possible pairs efficiently within the constraints, providing the correct result with a time complexity of O(n^2), which is acceptable given the input size.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks









































































































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)



























































































































![[DEALS] The All-in-One Microsoft Office Pro 2019 for Windows: Lifetime License + Windows 11 Pro Bundle (89% off) & Other Deals Up To 98% Off](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



























![Is this too much for a modular monolith system? [closed]](https://i.sstatic.net/pYL1nsfg.png)






















































































































_Andreas_Prott_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)



























































































![What features do you get with Gemini Advanced? [April 2025]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2024/02/gemini-advanced-cover.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)












![Apple Shares Official Trailer for 'Long Way Home' Starring Ewan McGregor and Charley Boorman [Video]](https://www.iclarified.com/images/news/97069/97069/97069-640.jpg)
![Apple Watch Series 10 Back On Sale for $299! [Lowest Price Ever]](https://www.iclarified.com/images/news/96657/96657/96657-640.jpg)
![EU Postpones Apple App Store Fines Amid Tariff Negotiations [Report]](https://www.iclarified.com/images/news/97068/97068/97068-640.jpg)
![Apple Slips to Fifth in China's Smartphone Market with 9% Decline [Report]](https://www.iclarified.com/images/news/97065/97065/97065-640.jpg)