1128. Number of Equivalent Domino Pairs

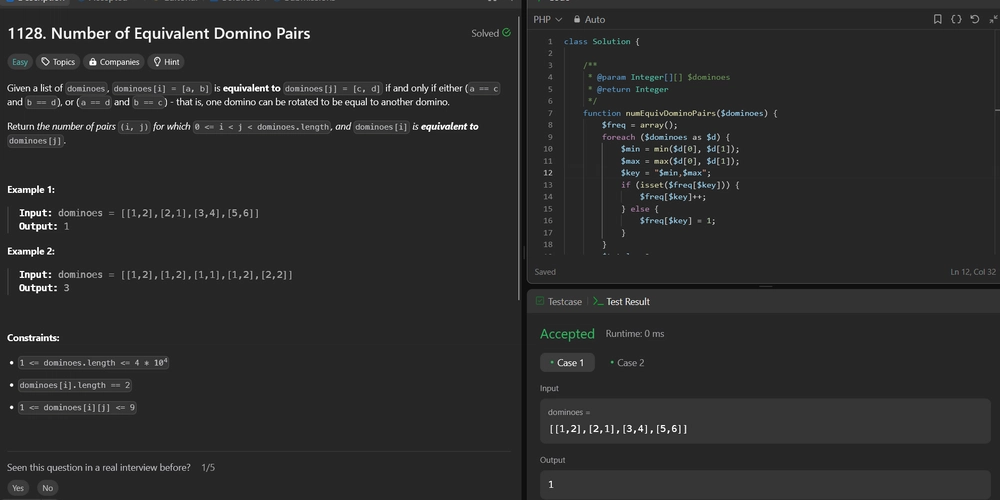
1128. Number of Equivalent Domino Pairs Difficulty: Easy Topics: Array, Hash Table, Counting Given a list of dominoes, dominoes[i] = [a, b] is equivalent to dominoes[j] = [c, d] if and only if either (a == c and b == d), or (a == d and b == c) - that is, one domino can be rotated to be equal to another domino. Return the number of pairs (i, j) for which 0

May 4, 2025 - 16:05

Difficulty: Easy

Topics: Array, Hash Table, Counting

Given a list of dominoes, dominoes[i] = [a, b] is equivalent to dominoes[j] = [c, d] if and only if either (a == c and b == d), or (a == d and b == c) - that is, one domino can be rotated to be equal to another domino.

Return the number of pairs (i, j) for which 0 <= i < j < dominoes.length, and dominoes[i] is equivalent to dominoes[j].

Example 1:

Input: dominoes = [[1,2],[2,1],[3,4],[5,6]]
Output: 1

Example 2:

Input: dominoes = [[1,2],[1,2],[1,1],[1,2],[2,2]]
Output: 3

Constraints:

1 <= dominoes.length <= 4 * 10⁴
dominoes[i].length == 2
1 <= dominoes[i][j] <= 9

Hint:

For each domino j, find the number of dominoes you've already seen (dominoes i with i < j) that are equivalent.
You can keep track of what you've seen using a hashmap.

Solution:

We need to determine the number of equivalent domino pairs in a given list of dominoes. Two dominoes are considered equivalent if one can be rotated to match the other. We can efficiently count these pairs using a hash map to track the frequency of each standardized domino form.

Approach

Standardize Domino Representation: For each domino [a, b], we standardize its representation by sorting the elements such that the smaller element comes first. This transforms each domino into a key (min(a, b), max(a, b)).
Frequency Counting: Use a hash map (or dictionary) to count the occurrences of each standardized domino key.
Calculate Pairs: For each unique domino key with a frequency c, the number of pairs is given by the combination formula c * (c - 1) / 2, which calculates the number of ways to choose 2 out of c items.

Let's implement this solution in PHP: 1128. Number of Equivalent Domino Pairs


/**
 * @param Integer[][] $dominoes
 * @return Integer
 */
function numEquivDominoPairs($dominoes) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example 1
$dominoes1 = [[1,2],[2,1],[3,4],[5,6]];
echo numEquivDominoPairs($dominoes1) . "\n"; // Output: 1

// Example 2
$dominoes2 = [[1,2],[1,2],[1,1],[1,2],[2,2]];
echo numEquivDominoPairs($dominoes2) . "\n"; // Output: 3
?>

Explanation:

Standardization: Each domino is converted into a standardized form to ensure that equivalent dominoes (like [1, 2] and [2, 1]) are treated identically. This is done by sorting the elements and forming a string key.
Frequency Counting: As we iterate through the list of dominoes, we maintain a count of how many times each standardized key appears.
Pair Calculation: Using the combination formula for each key's count, we sum up the total number of valid pairs. This formula efficiently calculates pairs without explicitly checking each possible pair, leading to an O(n) time complexity.

This approach ensures we efficiently count the equivalent pairs in linear time, making it suitable for large input sizes as specified in the problem constraints.

Contact Links

If you find this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks