Dev.to

1123. Lowest Common Ancestor of Deepest Leaves

1123. Lowest Common Ancestor of Deepest Leaves Difficulty: Medium Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree Given the root of a binary tree, return the lowest common ancestor of its deepest leaves. Recall that: The node of a binary tree is a leaf if and only if it has no children The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1. The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A. Example 1: Input: root = [3,5,1,6,2,0,8,null,null,7,4] Output: [2,7,4] Explanation: We return the node with value 2, colored in yellow in the diagram. The nodes coloured in blue are the deepest leaf-nodes of the tree. Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3. Example 2: Input: root = [1] Output: [1] Explanation: The root is the deepest node in the tree, and it's the lca of itself. Example 3: Input: root = [0,1,3,null,2] Output: [2] Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself. Constraints: The number of nodes in the tree will be in the range [1, 1000]. 0

Apr 4, 2025 - 02:14

Difficulty: Medium

Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree

Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

The node of a binary tree is a leaf if and only if it has no children
The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1.
The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A.

Example 1:

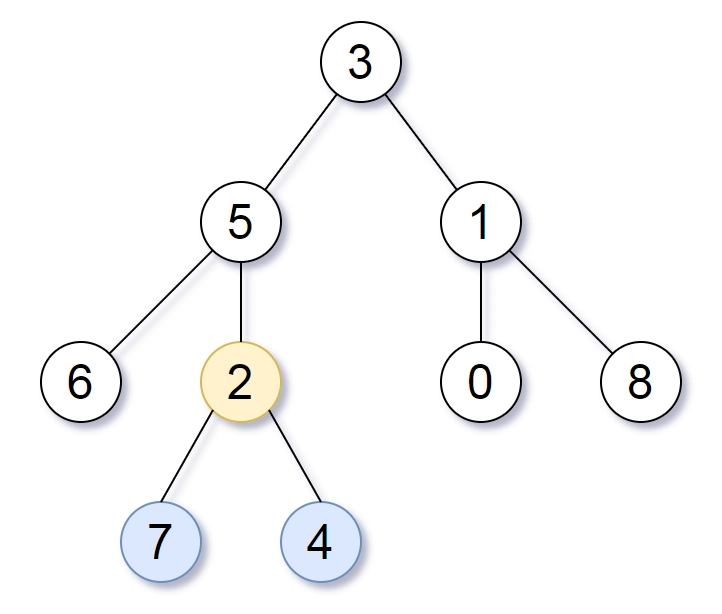
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
- The nodes coloured in blue are the deepest leaf-nodes of the tree.
- Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

Constraints:

The number of nodes in the tree will be in the range [1, 1000].
0 <= Node.val <= 1000
The values of the nodes in the tree are unique.

Note: This question is the same as 865. Smallest Subtree with all the Deepest Nodes

Hint:

Do a postorder traversal.
Then, if both subtrees contain a deepest leaf, you can mark this node as the answer (so far).
The final node marked will be the correct answer.

Solution:

We need to find the lowest common ancestor (LCA) of the deepest leaves in a binary tree. The LCA of a set of nodes is the node with the largest depth such that every node in the set is in the subtree rooted at this node. The deepest leaves are the leaves at the maximum depth in the tree.

Approach

The approach involves a post-order traversal of the tree. For each node, we compute the maximum depth of its left and right subtrees. If both subtrees have the same maximum depth, the current node is the LCA of the deepest leaves in its subtree. Otherwise, the LCA is derived from the subtree with the greater depth. This approach ensures that we efficiently determine the LCA without explicitly collecting all deepest leaves and then computing their LCA.

Let's implement this solution in PHP: 1123. Lowest Common Ancestor of Deepest Leaves


/**
 * @param TreeNode $root
 * @return TreeNode
 */
function lcaDeepestLeaves($root) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * @param $node
 * @param $depth
 * @return array
 */
function dfs($node, $depth) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test Cases
$testCases = [
    // Test Case 1
    [
        'input' => [3, 5, 1, 6, 2, 0, 8, null, null, 7, 4],
        'expected' => 2
    ],
    // Test Case 2
    [
        'input' => [1],
        'expected' => 1
    ],
    // Test Case 3
    [
        'input' => [0, 1, 3, null, 2],
        'expected' => 2
    ],
    // Test Case 4: Edge Case with one node
    [
        'input' => [10],
        'expected' => 10
    ],
    // Test Case 5: Larger tree with deeper leaves
    [
        'input' => [1, 2, 3, 4, 5, 6, 7, null, null, 8, 9],
        'expected' => 8
    ],
];

foreach ($testCases as $index => $testCase) {
    $input = $testCase['input'];
    $expected = $testCase['expected'];

    // Build the tree from the array
    $tree = buildTree($input);

    $result = lcaDeepestLeaves($tree);

    // Output the result
    echo "Test Case " . ($index + 1) . ":\n";
    echo "Input: " . implode(",", $input) . "\n";
    echo "Expected Output: " . $expected . "\n";
    echo "Output: " . $result->val . "\n\n";
}

//Output
Test Case 1:
Input: 3,5,1,6,2,0,8,,,
Expected Output: 2
Output: 2

Test Case 2:
Input: 1
Expected Output: 1
Output: 1

Test Case 3:
Input: 0,1,3,,2
Expected Output: 2
Output: 2

Test Case 4:
Input: 10
Expected Output: 10
Output: 10

Test Case 5:
Input: 1,2,3,4,5,6,7,,,8,9
Expected Output: 8
Output: 8

?>

Explanation:

Post-order Traversal: The function dfs performs a post-order traversal of the tree, starting from the root and moving to the leaves. This ensures that we process children before their parent nodes.
Depth Calculation: For each node, the depth is calculated and passed down recursively. If a node is a leaf, its depth is returned along with the node itself as the LCA.
Subtree Comparison: For each non-leaf node, we compare the maximum depths of its left and right subtrees. If one subtree is deeper, the LCA from the deeper subtree is propagated up. If both subtrees have the same depth, the current node becomes the LCA for its subtree.
Result Extraction: The root node's result is extracted, which gives the LCA of the deepest leaves in the entire tree.

This approach efficiently computes the LCA in O(n) time complexity, where n is the number of nodes in the tree, as each node is visited exactly once. The space complexity is O(h) due to the recursion stack, where h is the height of the tree.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks