ReRAM Revolution: Stochastic Computing Breakthrough for Edge Devices

This is a Plain English Papers summary of a research paper called ReRAM Revolution: Stochastic Computing Breakthrough for Edge Devices. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter. Revolutionizing Edge Computing: All-in-Memory Stochastic Computing using ReRAM As the demand for efficient, low-power computing in embedded and edge devices grows, traditional computing methods struggle with complex tasks under tight resource constraints. Stochastic Computing (SC) has emerged as a promising alternative, approximating complex arithmetic operations using simple bitwise operations on random bit-streams. However, conventional SC implementations face significant challenges—stochastic bit-stream generators consume over 80% of system power and area, while data movement between memory and processor creates additional overhead. Researchers have developed a novel approach that implements the entire SC flow within Resistive RAM (ReRAM) memory, leveraging the physical properties of ReRAM devices to achieve remarkable efficiency improvements. High-level overview of the proposed in-memory SC solution showing the ReRAM array, greater-than operation using basic logic gates, and write latches in peripheral circuitry. Understanding the Foundations: Background and Technology ReRAM-based Computing: The Building Blocks Resistive RAM (ReRAM) is a type of non-volatile memory where data is represented through resistance levels—high resistance state (HRS) for '0' and low resistance state (LRS) for '1'. These memory cells are organized in a 2D grid of rows (wordlines) and columns (bitlines). ReRAM offers several advantages for compute-in-memory applications: DRAM-comparable read performance Higher density than conventional memory Lower read energy consumption However, ReRAM also has limitations, including costly write operations that impact energy consumption and endurance. For compute-in-memory applications, 1T1R (one transistor, one resistor) crossbars are extensively used to perform analog matrix-vector multiplication in constant time. Logic operations can be implemented using techniques like MAGIC (Memristor-Aided loGIC) and scouting logic. Interestingly, ReRAM cells have inherent stochasticity and noise—a property typically considered a disadvantage but one that can be leveraged for generating true random numbers, as demonstrated in the Stoch-IMC: Bit-Parallel Stochastic In-Memory Computing approach. Stochastic Computing (SC): A Primer SC represents an unconventional approach to computing where data is encoded as probabilities in random bit-streams rather than using traditional binary representation. In SC, a value x ∈ [0,1] is encoded by the probability of a '1' appearing in a bit-stream. For example, the bit-stream '10101' represents the value 3/5, where 5 is the bit-stream length. This representation enables complex computations to be performed using simple logic gates: Multiplication: implemented with a single AND gate Addition: implemented with a multiplexer (MUX) Subtraction: implemented with an XOR gate Division: implemented with a MUX and D-flip-flop SC systems comprise three primary components: Bit-stream generator that converts data from binary to stochastic representation Computation logic that performs bit-wise operations Bit-stream to binary converter The quality of stochastic bit-streams (SBSs) is crucial for accuracy. Conventional SC systems use CMOS-based pseudo-random number generators (PRNGs) like linear-feedback shift registers (LFSRs), but these can lead to suboptimal performance as very long SBSs are needed for acceptable accuracy. Another critical aspect of SC is correlation control. Some operations (multiplication and addition) require uncorrelated inputs, while others (subtraction and division) need correlated inputs for correct functionality. State-of-the-art In-memory SC Solutions: Current Approaches Existing compute-in-memory (CIM) SC designs are mostly hybrid implementations. Some use memristive arrays to generate random numbers with CMOS logic for computations, while others do the reverse. For example, Knag et al. proposed generating SBSs using memristors with off-memory CMOS stochastic circuits for computation. Other approaches exploit the switching stochasticity of probabilistic Conductive Bridging RAM (CBRAM) devices to generate SBSs efficiently in memory. ReRAM-based SBS generation has also been explored, primarily using the probabilistic switching (write operation) in ReRAM. However, these methods face limitations: They're extremely slow They negatively affect write endurance They can generate SBSs with target probabilities but lack correlation control The Architectural Exploration of Application-Specific Resonant SRAM Compute paper explores alternative memory-based computing approaches, though with different underlying technologies. Novel Approach: In-ReRAM Sto

Apr 17, 2025 - 20:35

This is a Plain English Papers summary of a research paper called ReRAM Revolution: Stochastic Computing Breakthrough for Edge Devices. If you like these kinds of analysis, you should join AImodels.fyi or follow us on Twitter.

Revolutionizing Edge Computing: All-in-Memory Stochastic Computing using ReRAM

As the demand for efficient, low-power computing in embedded and edge devices grows, traditional computing methods struggle with complex tasks under tight resource constraints. Stochastic Computing (SC) has emerged as a promising alternative, approximating complex arithmetic operations using simple bitwise operations on random bit-streams. However, conventional SC implementations face significant challenges—stochastic bit-stream generators consume over 80% of system power and area, while data movement between memory and processor creates additional overhead.

Researchers have developed a novel approach that implements the entire SC flow within Resistive RAM (ReRAM) memory, leveraging the physical properties of ReRAM devices to achieve remarkable efficiency improvements.

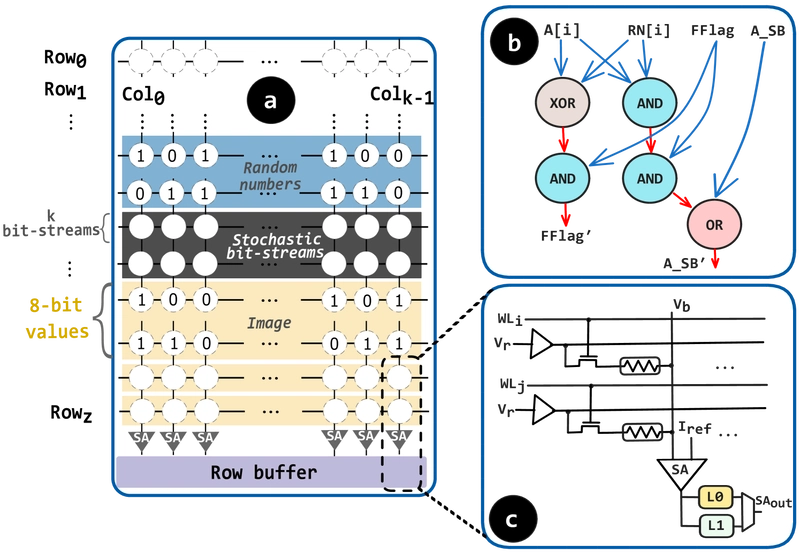
High-level overview of the proposed in-memory SC solution showing the ReRAM array, greater-than operation using basic logic gates, and write latches in peripheral circuitry.

Understanding the Foundations: Background and Technology

ReRAM-based Computing: The Building Blocks

Resistive RAM (ReRAM) is a type of non-volatile memory where data is represented through resistance levels—high resistance state (HRS) for '0' and low resistance state (LRS) for '1'. These memory cells are organized in a 2D grid of rows (wordlines) and columns (bitlines).

ReRAM offers several advantages for compute-in-memory applications:

DRAM-comparable read performance
Higher density than conventional memory
Lower read energy consumption

However, ReRAM also has limitations, including costly write operations that impact energy consumption and endurance. For compute-in-memory applications, 1T1R (one transistor, one resistor) crossbars are extensively used to perform analog matrix-vector multiplication in constant time. Logic operations can be implemented using techniques like MAGIC (Memristor-Aided loGIC) and scouting logic.

Interestingly, ReRAM cells have inherent stochasticity and noise—a property typically considered a disadvantage but one that can be leveraged for generating true random numbers, as demonstrated in the Stoch-IMC: Bit-Parallel Stochastic In-Memory Computing approach.

Stochastic Computing (SC): A Primer

SC represents an unconventional approach to computing where data is encoded as probabilities in random bit-streams rather than using traditional binary representation. In SC, a value x ∈ [0,1] is encoded by the probability of a '1' appearing in a bit-stream. For example, the bit-stream '10101' represents the value 3/5, where 5 is the bit-stream length.

This representation enables complex computations to be performed using simple logic gates:

Multiplication: implemented with a single AND gate
Addition: implemented with a multiplexer (MUX)
Subtraction: implemented with an XOR gate
Division: implemented with a MUX and D-flip-flop

SC systems comprise three primary components:

Bit-stream generator that converts data from binary to stochastic representation
Computation logic that performs bit-wise operations
Bit-stream to binary converter

The quality of stochastic bit-streams (SBSs) is crucial for accuracy. Conventional SC systems use CMOS-based pseudo-random number generators (PRNGs) like linear-feedback shift registers (LFSRs), but these can lead to suboptimal performance as very long SBSs are needed for acceptable accuracy.

Another critical aspect of SC is correlation control. Some operations (multiplication and addition) require uncorrelated inputs, while others (subtraction and division) need correlated inputs for correct functionality.

State-of-the-art In-memory SC Solutions: Current Approaches

Existing compute-in-memory (CIM) SC designs are mostly hybrid implementations. Some use memristive arrays to generate random numbers with CMOS logic for computations, while others do the reverse.

For example, Knag et al. proposed generating SBSs using memristors with off-memory CMOS stochastic circuits for computation. Other approaches exploit the switching stochasticity of probabilistic Conductive Bridging RAM (CBRAM) devices to generate SBSs efficiently in memory.

ReRAM-based SBS generation has also been explored, primarily using the probabilistic switching (write operation) in ReRAM. However, these methods face limitations:

They're extremely slow
They negatively affect write endurance
They can generate SBSs with target probabilities but lack correlation control

The Architectural Exploration of Application-Specific Resonant SRAM Compute paper explores alternative memory-based computing approaches, though with different underlying technologies.

Novel Approach: In-ReRAM Stochastic Computing Architecture

The researchers' approach exploits the physical properties of ReRAM arrays to implement all stages of the SC flow. Multiple arrays are used to parallelize and pipeline different stages of computation.

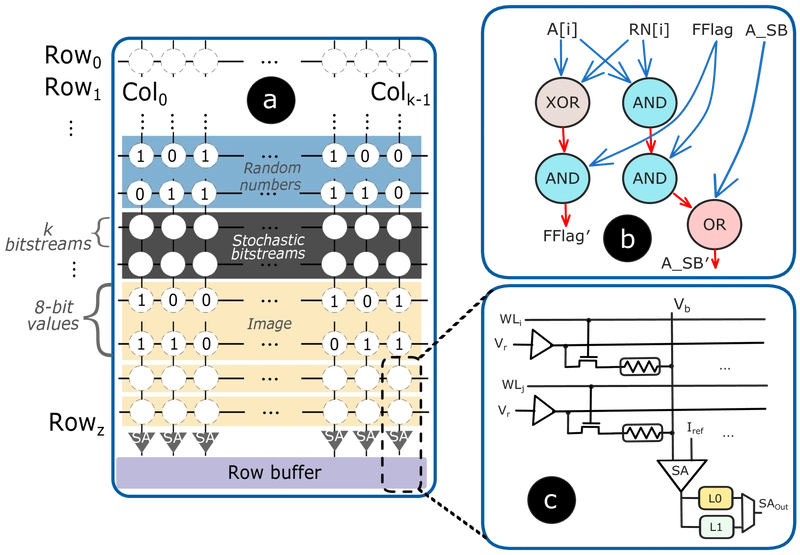
High-level overview of in-memory SC showing the SC flow, greater-than operation using basic logic gates, scaled addition in SC, CIM array for SC, and sensing circuitry.

Harnessing Noise: RNG using Read Disturbance

The inherent variability of ReRAM devices enables generating true random numbers. This approach utilizes the state instability of TaOx-based devices, which may be caused by electron trapping/detrapping or by oxygen vacancy relocation.

The random number generation process works by:

Applying a constant 0.2V bias to the device
Splitting the read instability signal and delaying half of it using an RC circuit
Comparing the delayed and non-delayed signals
Using the comparison result with a clock signal to generate a seed for a 4-bit nonlinear feedback shift register

This method achieves a generation rate of 35 kbit and meets the requirements of the NIST test for randomness.

Converting Binary to Stochastic: Efficient Number Generation

The system uses true random numbers stored directly in ReRAM arrays. To generate stochastic bit-streams from these random numbers (called in-memory SNG or IMSNG), it compares them with n-bit input binary operands using in-memory bitwise operations.

For comparing two binary numbers A and RN in memory:

Starting from the most significant bit (MSB) to the least significant bit (LSB)
Performing bitwise comparison and stopping at the first non-equal bit position
Implementing the greater-than operation using in-ReRAM bitwise XOR and AND operation with a flag bit

The result is a row ASB representing the stochastic bit-stream of A. This process is optimized using logic synthesis tools to convert the comparison network into efficient data structures.

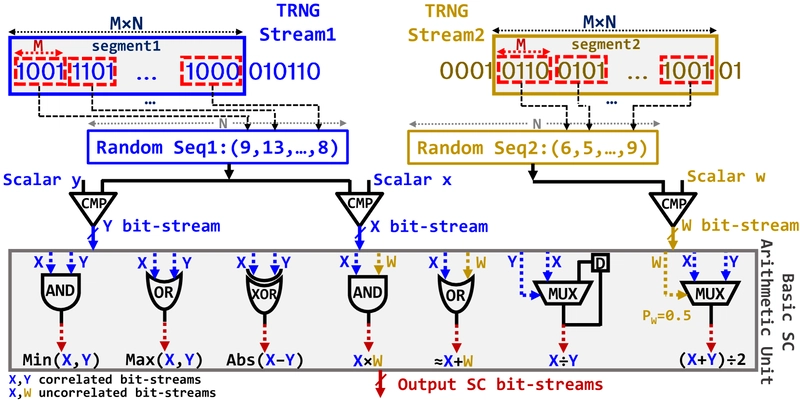
In-ReRAM SBS generation and SC arithmetic operations, showing CORDIV for SC division with X≤Y and addition with OR where inputs are in the [0,0.5] interval.

Computations in Memory: Stochastic Circuits using Scouting Logic

Scouting Logic (SL) implements boolean logic using ReRAM read operations with a modified sense amplifier. During a logic operation, multiple rows are simultaneously activated, and the resulting current through cells in each bitline is compared with a reference current by the sense amplifier.

Basic arithmetic operations are implemented using bulk bitwise logic schemes:

Multiplication: Implemented using bitwise AND with time complexity O(1)—a significant improvement over conventional binary multiplication with O(n²) complexity
Scaled Addition: Implemented using a 3-input majority gate (MAJ) with time complexity O(1), improving over both traditional binary addition and MUX-based SC addition with O(N) complexity
Division: Implemented using latch-based circuitry to create a JK flip-flop with time complexity O(N), better than CIM division methods on integer data requiring O(n²) write cycles
Other Operations: Approximate addition, absolute subtraction, minimum, and maximum implemented using OR, XOR, AND, and OR operations respectively

The Transverse Read Assisted Fast Valid Bits Collection approach offers complementary innovations in memory read techniques that could enhance this system further.

SC Operations	IMSNG [21]						Software -MATLAB									QRNG (Sobd)
	N:32	64	128	256	512	N:32	64	128	256	512	N:32	64	128	256	512	N:32	64	128	256	512
Multiplication	0.473	0.255	0.147	0.091	0.061	0.444	0.219	0.108	0.054	0.027	0.851	0.476	0.221	0.093	0.060	0.058	0.017	0.005	0.001	$2.9 \times 10^{-4}$
Scaled Addition	0.690	0.356	0.193	0.109	0.062	0.648	0.328	0.159	0.082	0.041	1.117	0.607	0.289	0.157	0.065	0.102	0.013	0.003	0.002	$2.1 \times 10^{-4}$
Approx. Addition	1.548	1.186	1.024	0.927	0.886	1.379	1.055	0.897	0.789	0.751	2.654	1.702	1.180	0.914	0.842	0.463	0.586	0.670	0.662	0.689
Abs. Subtraction	0.641	0.354	0.136	0.144	0.107	0.514	0.263	0.129	0.064	0.034	0.559	0.281	0.136	0.058	0.026	0.016	0.004	0.001	$2.5 \times 10^{-4}$	$6.5 \times 10^{-4}$
Division	1.614	0.895	0.518	0.295	0.187	1.454	0.789	0.392	0.196	0.106	2.760	2.140	1.688	1.630	1.477	0.251	0.164	0.129	0.126	0.128
Minimum	0.572	0.307	0.177	0.106	0.064	0.514	0.265	0.130	0.066	0.032	1.493	0.811	0.394	0.199	0.085	0.033	0.008	0.002	$5.1 \times 10^{-4}$	$1.3 \times 10^{-4}$
Maximum	0.572	0.302	0.186	0.117	0.077	0.543	0.259	0.132	0.064	0.033	0.481	0.263	0.123	0.073	0.027	0.032	0.008	0.002	$5.0 \times 10^{-4}$	$1.3 \times 10^{-4}$

Mean Squared Error (MSE) comparison for basic arithmetic operations in stochastic computing using different methods, showing how In-Memory Stochastic Number Generation (IMSNG) compares to other approaches across various bit-stream lengths.

Converting Results Back: Stochastic to Binary Conversion

The final step in the SC flow converts the output bit-stream back to binary representation. Instead of using CMOS counters for sequential counting, the researchers' approach achieves the count in a single step using bitline current accumulation:

The output bit-stream is applied as input voltages to a designated reference column
All cells in this column are pre-programmed to low resistance states
The total current through the bitline represents the population count of the bit-stream
This current is measured and digitized using analog-to-digital converters (ADCs)

This approach eliminates the need for sequential counting, significantly improving conversion efficiency.

Evaluation and Results: Performance in Real-World Applications

The system was evaluated using three image processing applications that demonstrate different aspects of stochastic computing operations:

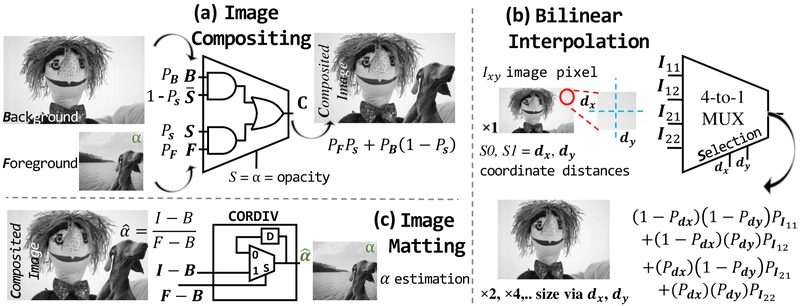
SC image processing applications: (a) Image Compositing, merging background and foreground images with α channel. (b) Bilinear Interpolation, up-scaling input images. (c) Image Matting, parsing α channel for the foreground object to separate the background.

Image Compositing: Merges background and foreground images using an alpha channel for opacity. The compositing formula C=F×α+B×(1-α) corresponds to a MUX operation in SC.
Bilinear Interpolation: Up-scales images by estimating new pixel values between existing ones. This uses a 4-to-1 MUX in SC, with bit-streams of neighboring pixels as inputs and relative distances as selection inputs.
Image Matting: Separates background and foreground by estimating the alpha channel. This operation involves division, implemented using the CORDIV design.

CMOS-based Design ( $\boldsymbol{)}$ )			Total Latency $\boldsymbol{\$}$	Total Energy $(\mathrm{nJ})$
Binary $\rightarrow$ SC $\boldsymbol{\Theta}$	SC arithmetic operations $\boldsymbol{\Theta}$	SC $\rightarrow$ Binary $\boldsymbol{\Theta}$
LFSR	Multiplication		122.88	0.23
$\checkmark$	Addition		130.56	0.26
Comparator	Subtraction		133.12	0.16
	Division		133.12	0.18
Sobol	Multiplication		125.44	0.30
$\checkmark$	Addition		130.56	0.30
Comparator	Subtraction		133.12	0.12
	Division		130.56	0.14
ReRAM-based Design ( $\boldsymbol{\dagger}$ )
IMSNG-opt	Multiplication		80.8	3.50
	Addition		80.8	3.50
	Subtraction	8-bit ADC [37]	81.6	3.51
	Division		12544.0	4.48

Performance comparison showing total latency and energy consumption for CMOS-based vs. ReRAM-based designs across different operations.

Design	Image Compositing		Bilinear Interpolation		Image Matting
	$\boldsymbol{\mathcal { R }}$	$\boldsymbol{\checkmark}$	$\boldsymbol{\mathcal { R }}$	$\boldsymbol{\checkmark}$	$\boldsymbol{\checkmark}$	$\checkmark$
$\triangleleft[35]$	99.9/91.8	82.9/42.4	95.6/39.0	64.4/37.6	99.9/50.3	4.8/-18.2
$\leftarrow 32$	99.9/23.4	99.9/22.2	82.0/28.5	79.4/28.6	95.3/31.5	88.2/30.0
$\leftarrow 64$	99.9/26.7	99.9/25.6	87.7/29.5	86.5/29.7	98.7/37.8	93.0/36.7
$\leftarrow 128$	99.9/28.2	99.9/27.6	91.4/30.2	90.0/29.7	99.4/41.7	94.6/38.5
$\leftarrow 256$	99.9/32.3	99.9/30.9	93.0/31.1	92.9/31.5	99.7/44.9	96.7/44.5

Accuracy results for image processing applications under different configurations, showing quality metrics across various bit-stream lengths.

The performance evaluation shows significant improvements:

Throughput improvements of 1.39× to 2.16× compared to state-of-the-art solutions
Energy consumption reductions of 1.15× to 2.8×
Average image quality drop of only 5% across multiple SBS lengths and image processing tasks

These results demonstrate the effectiveness of the all-in-memory stochastic computing approach for edge computing applications. The 65nm 8b-Activation 8b-Weight SRAM-Based approach offers an alternative SRAM-based perspective that could provide interesting comparisons for future work.

The research shows that by leveraging the physical properties of ReRAM for both random number generation and computation, it's possible to create highly efficient stochastic computing systems that eliminate data movement overhead while maintaining acceptable accuracy for real-world applications.

Click here to read the full summary of this paper