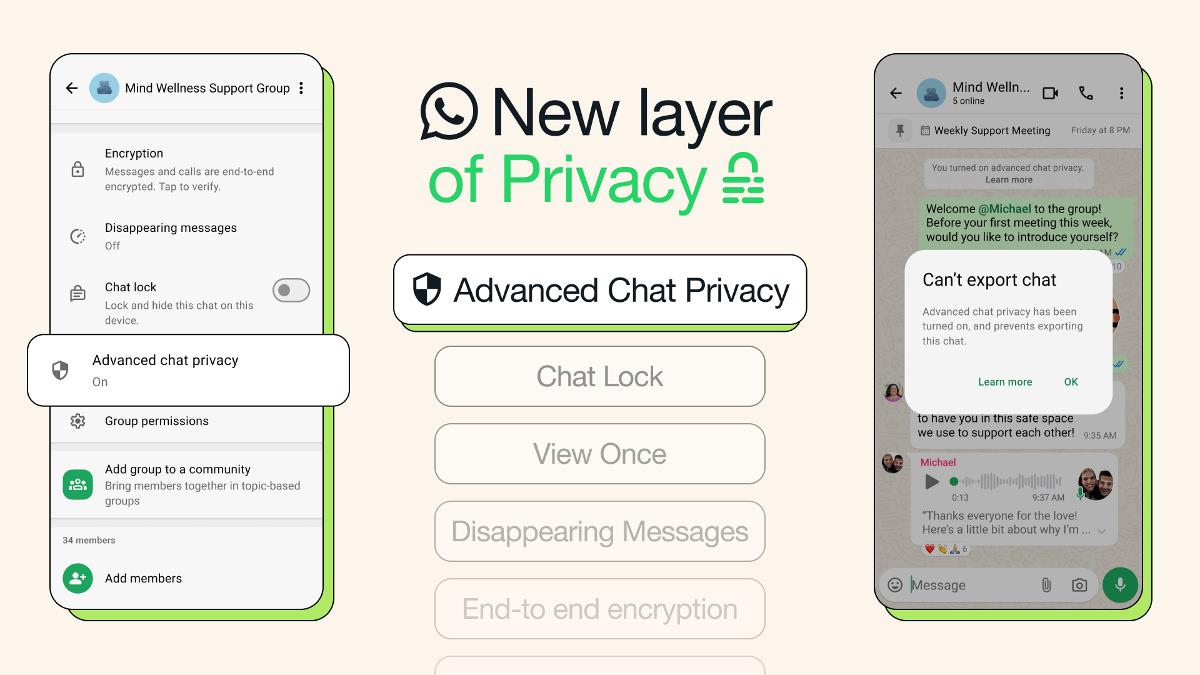
Leetcode - 117. Populating Next Right Pointers in Each Node II

Approach The breadth-first search (BFS) approach is ideal for this problem. By performing a level order traversal, we can easily traverse all nodes level by level, ensuring that we can connect each node to its next node in constant time. Here’s a step-by-step breakdown of the approach: 1. Level Order Traversal The key to solving this problem is traversing the tree level by level. We can use a queue to maintain the current level's nodes. For each level: We dequeue nodes from the queue, one by one. For each node (except the last one on the level), we link it to the next node in the queue by setting the next pointer. We then enqueue the left and right children of each node to the queue, if they exist. This ensures that all nodes on the next level will be processed in the next iteration. 2. Implementation Here’s the code implementation of the approach: var connect = function (root) { if (!root) return root; let queue = [root]; // Start with the root node in the queue. while (queue.length > 0) { let levelSize = queue.length; // Get the size of the current level. // Iterate over all nodes at the current level for (let i = 0; i

Apr 24, 2025 - 21:16

Leetcode - 117. Populating Next Right Pointers in Each Node II

Approach

The breadth-first search (BFS) approach is ideal for this problem. By performing a level order traversal, we can easily traverse all nodes level by level, ensuring that we can connect each node to its next node in constant time.

Here’s a step-by-step breakdown of the approach:

1. Level Order Traversal

The key to solving this problem is traversing the tree level by level. We can use a queue to maintain the current level's nodes. For each level:

We dequeue nodes from the queue, one by one.
For each node (except the last one on the level), we link it to the next node in the queue by setting the next pointer.
We then enqueue the left and right children of each node to the queue, if they exist. This ensures that all nodes on the next level will be processed in the next iteration.

2. Implementation

Here’s the code implementation of the approach:

var connect = function (root) {
    if (!root) return root;

    let queue = [root];  // Start with the root node in the queue.

    while (queue.length > 0) {
        let levelSize = queue.length;  // Get the size of the current level.

        // Iterate over all nodes at the current level
        for (let i = 0; i < levelSize; i++) {
            let rootNode = queue.shift();  // Dequeue a node.

            // Connect the node to the next node in the same level.
            if (i < levelSize - 1) {
                rootNode.next = queue[0];  // The next node in the queue.
            }

            // Enqueue left and right children of the current node (if any).
            if (rootNode.left !== null) {
                queue.push(rootNode.left);
            }
            if (rootNode.right !== null) {
                queue.push(rootNode.right);
            }
        }
    }

    return root;  // Return the root node with all next pointers connected.
};

Explanation

Queue Initialization:

We begin by initializing a queue with the root node. The queue will help us traverse each level of the tree in breadth-first fashion.
Level Traversal:

We calculate the size of the current level (levelSize). This helps us to ensure that we only link nodes that are on the same level.
Connecting Nodes:

For each node, we check if it is the last node at the current level (i.e., i < levelSize - 1). If it’s not the last node, we set its next pointer to the next node in the queue.
Enqueue Children:

After processing each node, we enqueue its left and right children (if they exist). This ensures that the next level of nodes will be processed in the next iteration.
Return the Root:

Once all the levels have been processed, we return the root of the tree. Now, each node's next pointer is correctly set.

Time Complexity

The time complexity of this algorithm can be analyzed as follows:

Level Traversal:

The algorithm performs a level-order traversal of the tree, visiting each node exactly once. Since there are N nodes in the tree, we perform N operations in total.
Queue Operations:

Each node is added and removed from the queue exactly once. Each enqueue and dequeue operation takes O(1) time.

Thus, the total time complexity is:

O(N)

Where N is the total number of nodes in the tree.

Space Complexity

The space complexity is determined by the amount of space used by the queue:

In the worst case, the queue holds the maximum number of nodes at any level, which is the bottom level of a perfect binary tree. For a perfect binary tree, the number of nodes at the bottom level is N / 2.

Thus, the space complexity is:

O(N)

Where N is the total number of nodes in the tree.

Conclusion

This approach efficiently solves the problem of populating the next pointers in a perfect binary tree using a level-order traversal (BFS). The algorithm runs in O(N) time and uses O(N) space, making it optimal for this problem.