Introducción al PCA

En la actualidad, los datos son uno de los recursos más valiosos. Nos ayudan a encontrar patrones, tomar decisiones e incluso predecir el futuro. Pero, como hay tantos datos, analizarlos uno por uno no es práctico. Con PCA, podemos representar la información de muchas variables en solo unas pocas que siguen siendo útiles y representativas. ¿Qué es el análisis de componentes principales? El análisis de componentes principales (PCA, por sus siglas en inglés: Principal Components Analysis) es una técnica que reduce la cantidad de variables sin perder demasiada información. Se puede entender desde tres enfoques: Enfoque descriptivo: consiste en trazar una línea que atraviesa los puntos de los datos de forma que estén lo más cerca posible de esa línea. Así, se puede observar una dirección general de los datos. Fuente: https://cutt.ly/AmJ3I9M Enfoque estadístico: busca transformar muchas variables en unas pocas, tratando de que estas nuevas variables tengan la mayor variación posible. > La varianza es una medida que indica qué tanto varían los valores respecto a su promedio. Este enfoque se explica más adelante en la sección Enfoque estadístico. Enfoque geométrico: representa visualmente los datos en gráficas, proyectándolos en planos en 2D o 3D para observar sus relaciones. El propósito del PCA es obtener nuevas variables que resuman la información de muchas originales. Se parte de tener p variables medidas en n elementos. Esto se organiza en una matriz X de tamaño n x p: X = | p-variables₁₁ p-variables₁₂ ... p-variables₁n | | n-elementos₂₁ n-elementos₂₂ ... n-elementos₂n | | ⋮ ⋮ ⋱ ⋮ | | n-elementosₙ₁ n-elementosₙ₂ ... n-elementosₙn | El objetivo es reducir estas p columnas a un número menor, digamos r, donde r < p, y aun así conservar la mayoría de la información. Por ejemplo: si tienes una tabla con 5 columnas, el PCA puede convertirla en una tabla de solo 2 columnas que sigan representando la mayoría de los datos originales. ¿Cómo surge el PCA? Es difícil identificar un único origen del PCA, ya que distintos científicos trabajaron en ideas similares. En general, se buscaba encontrar líneas o planos que representaran bien los datos. Karl Pearson propuso métodos que, con la ayuda de la computación moderna, ahora se pueden aplicar fácilmente. Según Sánchez, los cuatro trabajos más importantes en los inicios del PCA fueron: Anderson: muy teórico, analiza muestras de componentes principales. Rao: aporta ideas sobre cómo interpretar y usar el PCA. Gower: trabaja con combinaciones del PCA y otras técnicas. Jeffers: compara resultados en casos prácticos. El PCA es versátil porque no necesita saber para qué se usarán los datos, lo que lo hace útil en muchos campos. Enfoque estadístico Según Castillo González, se pueden representar puntos de muchas dimensiones usando menos variables, siempre que se mantenga la mayoría de la información original. Esto se logra al encontrar nuevas variables (componentes) con la mayor varianza posible y que no estén relacionadas entre sí (no correlacionadas). Planos principales Cuando trabajamos con muchos datos, a veces queremos verlos en un gráfico para entender mejor cómo se agrupan o se diferencian. Por ejemplo, si tenemos las calificaciones de varios estudiantes en distintas materias, el PCA nos permite dibujar un plano, donde cada estudiante aparece como un punto, según sus resultados. Ese gráfico se llama plano principal y muestra la posición de cada individuo (persona, producto, etc.) según dos nuevas variables que el PCA calcula: las componentes principales. Cada punto en ese plano tiene dos coordenadas, como si fuera un punto en el plano cartesiano: (c_{i}^{1}, c_{i}^{2}) ( c_i^1 ) es la posición del individuo ( i ) en la primera componente principal. ( c_i^2 ) es su posición en la segunda componente principal. Estas coordenadas se calculan con fórmulas sencillas: c_{i}^{1} = x_i^T u_1 c_{i}^{2} = x_i^T u_2 ( x_i ): es el vector de datos del individuo ( i ) (por ejemplo, las notas de Pedro en varias materias). ( x_i^T ): es la transpuesta de ese vector (simplemente lo giramos para que se pueda multiplicar). ( u_1 ) y ( u_2 ): son los vectores de dirección de las primeras dos componentes principales. Se calculan en el proceso del PCA. Antes de hacer estos cálculos, los datos deben estar centrados y estandarizados, es decir, restando la media y dividiendo entre la desviación estándar. Esto asegura que todas las variables tengan la misma importancia. Ejemplo Tenemos las notas de Pedro y Sonia. Después de aplicar PCA, obtenemos las siguientes coordenadas: Pedro → (0.67, 1.64) Sonia → (3.04, 1.25) Eso significa que Pedro y Sonia aparecen como puntos en un gráfico, en posiciones diferentes según su rendimiento. Imagen 1: Primer plano principal para la tabla de notas escolares [Fuente: A

Apr 13, 2025 - 18:16

En la actualidad, los datos son uno de los recursos más valiosos. Nos ayudan a encontrar patrones, tomar decisiones e incluso predecir el futuro. Pero, como hay tantos datos, analizarlos uno por uno no es práctico.

Con PCA, podemos representar la información de muchas variables en solo unas pocas que siguen siendo útiles y representativas.

¿Qué es el análisis de componentes principales?

El análisis de componentes principales (PCA, por sus siglas en inglés: Principal Components Analysis) es una técnica que reduce la cantidad de variables sin perder demasiada información. Se puede entender desde tres enfoques:

Enfoque descriptivo: consiste en trazar una línea que atraviesa los puntos de los datos de forma que estén lo más cerca posible de esa línea. Así, se puede observar una dirección general de los datos.

Fuente: https://cutt.ly/AmJ3I9M

Enfoque estadístico: busca transformar muchas variables en unas pocas, tratando de que estas nuevas variables tengan la mayor variación posible. > La varianza es una medida que indica qué tanto varían los valores respecto a su promedio.

Este enfoque se explica más adelante en la sección Enfoque estadístico.

Enfoque geométrico: representa visualmente los datos en gráficas, proyectándolos en planos en 2D o 3D para observar sus relaciones.

El propósito del PCA es obtener nuevas variables que resuman la información de muchas originales. Se parte de tener p variables medidas en n elementos.

Esto se organiza en una matriz X de tamaño n x p:

X = | p-variables₁₁  p-variables₁₂  ...  p-variables₁n |
    | n-elementos₂₁ n-elementos₂₂ ...  n-elementos₂n |
    |     ⋮              ⋮          ⋱         ⋮       |
    | n-elementosₙ₁ n-elementosₙ₂ ...  n-elementosₙn |

El objetivo es reducir estas p columnas a un número menor, digamos r, donde r < p, y aun así conservar la mayoría de la información.

Por ejemplo: si tienes una tabla con 5 columnas, el PCA puede convertirla en una tabla de solo 2 columnas que sigan representando la mayoría de los datos originales.

¿Cómo surge el PCA?

Es difícil identificar un único origen del PCA, ya que distintos científicos trabajaron en ideas similares. En general, se buscaba encontrar líneas o planos que representaran bien los datos.

Karl Pearson propuso métodos que, con la ayuda de la computación moderna, ahora se pueden aplicar fácilmente.

Según Sánchez, los cuatro trabajos más importantes en los inicios del PCA fueron:

Anderson: muy teórico, analiza muestras de componentes principales.
Rao: aporta ideas sobre cómo interpretar y usar el PCA.
Gower: trabaja con combinaciones del PCA y otras técnicas.
Jeffers: compara resultados en casos prácticos.

El PCA es versátil porque no necesita saber para qué se usarán los datos, lo que lo hace útil en muchos campos.

Enfoque estadístico

Según Castillo González, se pueden representar puntos de muchas dimensiones usando menos variables, siempre que se mantenga la mayoría de la información original.

Esto se logra al encontrar nuevas variables (componentes) con la mayor varianza posible y que no estén relacionadas entre sí (no correlacionadas).

Planos principales

Cuando trabajamos con muchos datos, a veces queremos verlos en un gráfico para entender mejor cómo se agrupan o se diferencian.

Por ejemplo, si tenemos las calificaciones de varios estudiantes en distintas materias, el PCA nos permite dibujar un plano, donde cada estudiante aparece como un punto, según sus resultados.

Ese gráfico se llama plano principal y muestra la posición de cada individuo (persona, producto, etc.) según dos nuevas variables que el PCA calcula: las componentes principales.

Cada punto en ese plano tiene dos coordenadas, como si fuera un punto en el plano cartesiano:

(c_{i}^{1}, c_{i}^{2})

( c_i^1 ) es la posición del individuo ( i ) en la primera componente principal.
( c_i^2 ) es su posición en la segunda componente principal.

Estas coordenadas se calculan con fórmulas sencillas:

c_{i}^{1} = x_i^T u_1  
c_{i}^{2} = x_i^T u_2

( x_i ): es el vector de datos del individuo ( i ) (por ejemplo, las notas de Pedro en varias materias).
( x_i^T ): es la transpuesta de ese vector (simplemente lo giramos para que se pueda multiplicar).
( u_1 ) y ( u_2 ): son los vectores de dirección de las primeras dos componentes principales. Se calculan en el proceso del PCA.

Antes de hacer estos cálculos, los datos deben estar centrados y estandarizados, es decir, restando la media y dividiendo entre la desviación estándar. Esto asegura que todas las variables tengan la misma importancia.

Ejemplo

Tenemos las notas de Pedro y Sonia. Después de aplicar PCA, obtenemos las siguientes coordenadas:

Pedro → (0.67, 1.64)
Sonia → (3.04, 1.25)

Eso significa que Pedro y Sonia aparecen como puntos en un gráfico, en posiciones diferentes según su rendimiento.

Imagen 1: Primer plano principal para la tabla de notas escolares

[Fuente: Análisis Multivariado de Datos, Métodos y Aplicaciones]

Círculos de correlaciones (versión sencilla con fórmula)

Una vez que tenemos el plano principal, también podemos ver cómo se relacionan las variables originales (por ejemplo, matemáticas, español, ciencias) con las nuevas componentes calculadas por el PCA.

Cada variable original ( x^j ) tiene una "posición" en relación con una componente principal ( c^k ). Esa posición se calcula con:

r(x^j, c^k)

Esto es simplemente la correlación entre la variable original y la componente principal. Nos dice qué tanto esa variable está alineada con esa dirección principal de los datos.

Ejemplo

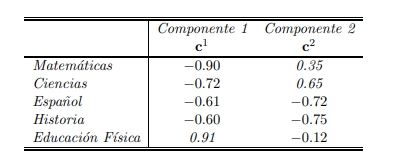
En el caso de las calificaciones, podríamos tener una tabla como esta:

Imagen 2: Correlaciones entre materias y componentes principales

[Fuente: Análisis Multivariado de Datos, Métodos y Aplicaciones]

Esta tabla se puede convertir en un gráfico de círculo, donde las materias se ubican como flechas. Así podemos ver cuáles materias están relacionadas entre sí y cuáles influyen más en la forma del gráfico.

Interpretación de los resultados

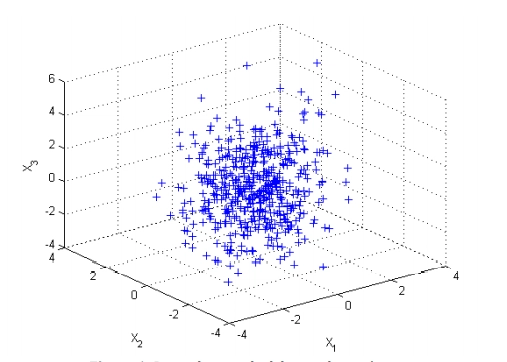
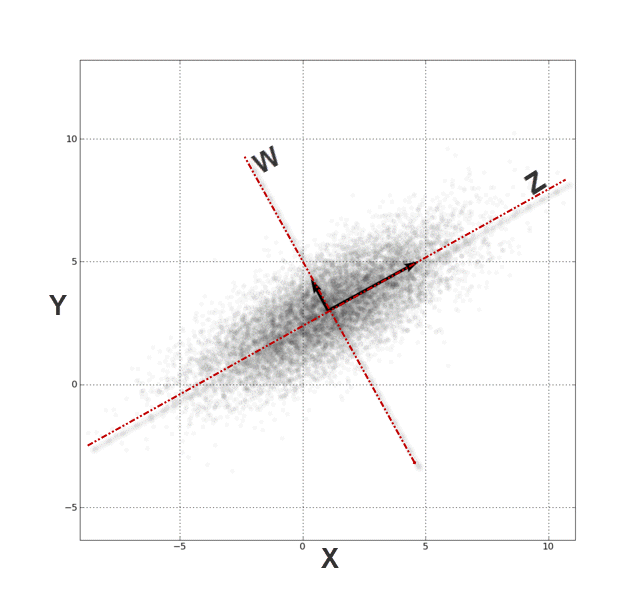
Una forma de entender el PCA es visualizar cómo se proyectan los datos. Imagina tener dos variables (X₁, X₂). El PCA busca la dirección donde los datos se dispersan más (componente Z₁):

Figura: Ilustración del vector Z₁

[Fuente: Análisis Multivariado de Datos, Métodos y Aplicaciones]

Luego, busca otra dirección (Z₂) que sea perpendicular a la anterior y también tenga mucha variación, pero sin repetir la información de Z₁:

Figura: Ilustración del vector Z₂

[Fuente: Análisis Multivariado de Datos, Métodos y Aplicaciones]

Interpretación de componentes

Interpretar los resultados del PCA es clave. Aunque se necesita experiencia, algunas guías pueden ayudar a encontrar patrones importantes en los datos.

Referencias

Andrés Sánchez Mangas. Análisis de componentes principales: Versiones dispersas y robustas al ruido impulsivo. Proyecto Fin de Carrera, Universidad Carlos III de Madrid, 2012.
W. Castillo, J. González, J. Trejos. Análisis Multivariado de Datos, Métodos y Aplicaciones. Centro de Investigaciones en Matemáticas Pura y Aplicada, Universidad de Costa Rica, Costa Rica, 2009.
Oldemar Rodríguez Rojas. Análisis en componentes principales. Universidad de Costa Rica, San José, 2009.