How Cosine Similarity Helped My CLI Decide Where Files Belong (messy-folder-reorganizer-ai)
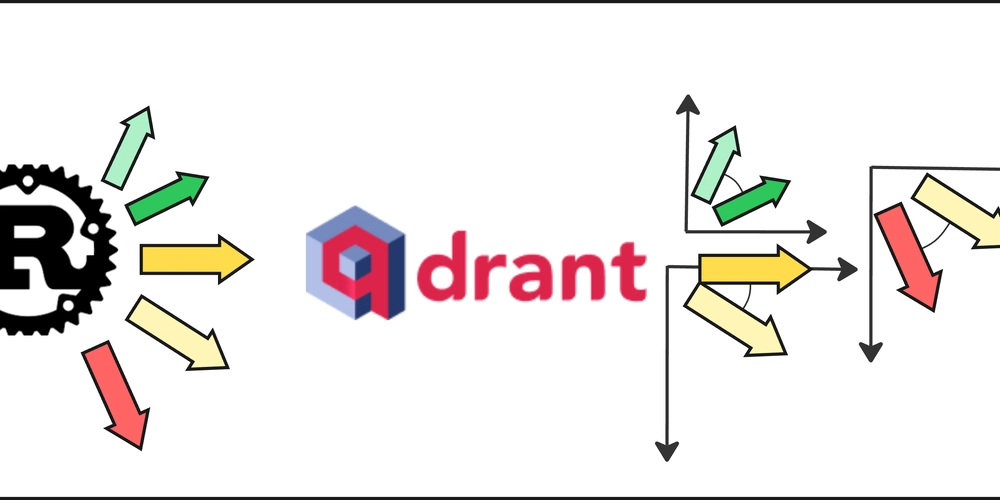
Introduction In version 0.2 of messy-folder-reorganizer-ai, I used the Qdrant vector database to search for similar vectors. This was necessary to determine which folder a file should go into based on its embedding. Because of this, I needed to revisit different distance/similarity metrics and choose the most appropriate one. Choosing the Right Vector Similarity Metric in Qdrant Qdrant supports the following distance/similarity metrics: Dot Product Cosine Similarity Euclidean Distance Manhattan Distance Distance/Similarity Formulas Let x and y be two vectors of dimensionality n. Cosine Similarity cosine(x, y) = (x · y) / (‖x‖ · ‖y‖) Dot Product dot(x, y) = Σ (xᵢ * yᵢ) ⚠️ If vectors are normalized to unit length, then: cosine(x, y) = dot(x, y) Euclidean Distance euclidean(x, y) = sqrt(Σ (xᵢ - yᵢ)²) Manhattan Distance (L1) manhattan(x, y) = Σ |xᵢ - yᵢ| When working with high-dimensional vectors (e.g., 1024 dimensions, as in the mxbai-embed-large:latest Ollama model) that have small magnitudes, Cosine Similarity is often the best choice — especially for embeddings. Why Cosine Similarity is a Good Choice Focuses on orientation, not magnitude Cosine similarity measures the angle between vectors. It tells you how similar the directions are*, regardless of vector length. This is useful when comparing embeddings, where absolute length may not be meaningful. Built-in normalization Cosine similarity is equivalent to the dot product of L2- normalized vectors, which helps reduce the effect of the "curse of dimensionality." Great for semantic embeddings Works very well when vectors represent meaning or context. Many models (e.g., OpenAI, BERT, Sentence Transformers) are trained with cosine similarity in mind. Efficient Can be computed quickly even in high dimensions. Cosine Similarity in Detail Imagine two arrows (vectors) starting from the origin in a multi-dimensional space. Cosine similarity measures the angle between them: If they point in exactly the same direction, similarity = 1.0 If they are completely opposite, similarity = -1.0 If they are orthogonal (90° apart), similarity = 0.0 The closer the angle is to zero, the more similar the vectors are. Formula Given two vectors A and B, cosine similarity is calculated as: cos(θ) = (A · B) / (||A|| * ||B||) A · B is the dot product of the vectors ||A|| and ||B|| are the magnitudes (lengths) of the vectors Example Let's take two simple 2D vectors: A = [1, 2] B = [2, 3] 1. Dot Product: A · B = (1 * 2) + (2 * 3) = 2 + 6 = 8 2. Magnitudes: ||A|| = √(1² + 2²) = √5 ≈ 2.236 ||B|| = √(2² + 3²) = √13 ≈ 3.606 3. Cosine Similarity: cos(θ) = 8 / (2.236 * 3.606) ≈ 8 / 8.062 ≈ 0.993 Result: 0.993 — Very high similarity! In the Context of the CLI In messy-folder-reorganizer-ai, embeddings represent file and folder names. Cosine similarity allows the CLI to: Find files with similar meaning or content Group files together Match files to folder "themes" based on vector similarity Looking for Feedback I’d really appreciate any feedback — positive or critical — on the project, the codebase, the article series, or the general approach used in the CLI. Thanks for Reading! Feel free to reach out here or connect with me on: GitHub LinkedIn Or just drop me a note if you want to chat about Rust, AI, or creative ways to clean up messy folders!
Introduction
In version 0.2 of messy-folder-reorganizer-ai, I used the Qdrant vector database to search for similar vectors. This was necessary to determine which folder a file should go into based on its embedding. Because of this, I needed to revisit different distance/similarity metrics and choose the most appropriate one.
Choosing the Right Vector Similarity Metric in Qdrant
Qdrant supports the following distance/similarity metrics:
- Dot Product
- Cosine Similarity
- Euclidean Distance
- Manhattan Distance
Distance/Similarity Formulas
Let x and y be two vectors of dimensionality n.
Cosine Similarity
cosine(x, y) = (x · y) / (‖x‖ · ‖y‖)
Dot Product
dot(x, y) = Σ (xᵢ * yᵢ)
⚠️ If vectors are normalized to unit length, then:
cosine(x, y) = dot(x, y)
Euclidean Distance
euclidean(x, y) = sqrt(Σ (xᵢ - yᵢ)²)
Manhattan Distance (L1)
manhattan(x, y) = Σ |xᵢ - yᵢ|
When working with high-dimensional vectors (e.g., 1024 dimensions, as in the mxbai-embed-large:latest Ollama model) that have small magnitudes, Cosine Similarity is often the best choice — especially for embeddings.
Why Cosine Similarity is a Good Choice
Focuses on orientation, not magnitude
Cosine similarity measures the angle between vectors. It tells you
how similar the directions are*, regardless of vector length. This
is useful when comparing embeddings, where absolute length may not
be meaningful.
Built-in normalization
Cosine similarity is equivalent to the dot product of L2-
normalized vectors, which helps reduce the effect of the "curse
of dimensionality."
Great for semantic embeddings
Works very well when vectors represent meaning or context. Many models (e.g., OpenAI, BERT, Sentence Transformers) are trained
with cosine similarity in mind.
Efficient
Can be computed quickly even in high dimensions.
Cosine Similarity in Detail
Imagine two arrows (vectors) starting from the origin in a multi-dimensional space. Cosine similarity measures the angle between them:
- If they point in exactly the same direction, similarity =
1.0 - If they are completely opposite, similarity =
-1.0 - If they are orthogonal (90° apart), similarity =
0.0
The closer the angle is to zero, the more similar the vectors are.
Formula
Given two vectors A and B, cosine similarity is calculated as:
cos(θ) = (A · B) / (||A|| * ||B||)
-
A · Bis the dot product of the vectors -
||A||and||B||are the magnitudes (lengths) of the vectors
Example
Let's take two simple 2D vectors:
A = [1, 2] B = [2, 3]
1. Dot Product:
A · B = (1 * 2) + (2 * 3) = 2 + 6 = 8
2. Magnitudes:
||A|| = √(1² + 2²) = √5 ≈ 2.236 ||B|| = √(2² + 3²) = √13 ≈ 3.606
3. Cosine Similarity:
cos(θ) = 8 / (2.236 * 3.606) ≈ 8 / 8.062 ≈ 0.993
Result: 0.993 — Very high similarity!
In the Context of the CLI
In messy-folder-reorganizer-ai, embeddings represent file and folder names. Cosine similarity allows the CLI to:
- Find files with similar meaning or content
- Group files together
- Match files to folder "themes" based on vector similarity
Looking for Feedback
I’d really appreciate any feedback — positive or critical — on the project, the codebase, the article series, or the general approach used in the CLI.
Thanks for Reading!
Feel free to reach out here or connect with me on:
Or just drop me a note if you want to chat about Rust, AI, or creative ways to clean up messy folders!









































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)

























































































































![[FREE EBOOKS] The Kubernetes Bible, The Ultimate Linux Shell Scripting Guide & Four More Best Selling Titles](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)






































































































.png?#)




.jpg?#)
































_Christophe_Coat_Alamy.jpg?#)


































































































![Rapidus in Talks With Apple as It Accelerates Toward 2nm Chip Production [Report]](https://www.iclarified.com/images/news/96937/96937/96937-640.jpg)