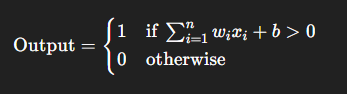How a neural network can learn any function
This blog focuses on showing how a neural network can learn any continuous function, The Universal Approximation Theorem. Universal Approximation Theorem Formally, Universal Approximation Theorem states that, In simple words, it means that, A feedforward neural network with a single hidden layer containing a finite number of neurons can approximate any continuous function on compact subsets of ℝⁿ, under mild assumptions on the activation function. This blog aims in giving a visualization on how the theorem works. Perceptron A perceptron is the most fundamental part of deep learning. Perceptron is a unit, that takes in ‘n’ inputs say x1, x2…. xn and each input has a weight associated with it say w1, w2, w3…wn and a bias term say ‘b’. The perceptron has two parts, a summation part that adds up all the weight * input and another layer that has an activation layer that determines the final output of the perceptron after applying non linearity. Lets consider a simple activation function (step function) Lets consider a simple perceptron with two inputs x1, x2 ∈ {0,1} and corresponding weights w1, w2. The perceptron can be used to learn 2 input boolean function. There are 16 two input boolean functions. Learning 2 input boolean functions using perceptron: In the above image, θ : b x1, x2,x3 : inputs Step function is used for σ We can notice that, a perceptron with step function as activation is basically a function that separates the plane into two parts and outputs 0 for one half and 1 for the other. Basically, a perceptron can be used to represent a ‘linearly separable’ function. Now.., are all the 16 two input binary functions linearly separable? No. Let us consider the case of XOR function, We can see, the function is not linearly separable. Hence, we cannot use a single perceptron to learn XOR. Among all the two input binary functions, only XOR and XNOR are non linearly separable. How a network of perceptrons can solve this issue. As per the universal approximation theorem, a network with single layer of perceptrons should be able to learn all the functions. Consider the below network: Lets understand whats going on, Let us name the perceptrons as P1, P2, P3, P4. P1 is activated only if x1, x2 are -1, -1 P2 is activated only if x1, x2 are -1, 1 P3 is activated only if x1, x2 are 1, -1 P4 is activated only if x1, x2 are 1, 1 So, at one given input, only one perceptron is activated. In a sense, its like, the input space is divided into multiple parts and divided among the perceptrons. This network can learn any two input boolean function linearly separable or not. Similarly, this is for 3 input boolean functions, Feed forward neural networks So.., how can we relate whatever we understood until now to a real valued continuous function that can be learnt by a feed forward neural network? Let us try to build a layer that can learn the function using the observations we made before. In a feed forward neural network, sigmoidal neurons are used ie sigmoid function is used as activation. We somehow have to make it to that one neuron activates only if the input lies in its input space. Even if that is somehow taken care of, we have to make it so that the neuron learns only the inputs in that input space? Considering an arbitrary function, we can divide the function into multiple parts and the number of parts is proportional to the number of neurons in the layer. Notice, how many ever finite parts we divide the function into, there is always an error which the Universal Approximation theorem considers as ε. How can a sigmoidal neuron be used to replicate the above required scenario? This is the sigmoid function and we know that, tweaking the ‘w’ changes the slope and tweaking the ‘b’ changes the position of the function on x axis. Increasing the value of w, we get something like this, Consider two sigmoidal functions y1, y2, Considering y3 = y2 - y1, We got what we wanted !!! This creates a tower like structure for required input range (tweaking b), by using multiple sigmoidal neurons like this, we can approximately create the required function. Let us call this function that creates the required structure as “tower function” Representing the tower function as a network. Finally, Using multiple of these tower functions, each tower gets activated only if the input lies in its input range. Same as what happened in the case of perceptrons while learning two input boolean functions. This concept can be extended to 3D space, where 3D tower functions can approximately represent the 3D function. Creating 3D tower functions is visualized below, To get the tower, we have to extract the red part, ie if its 1 I want it else I dont. We can pass it through a sigmoid closest to step function to achieve this. Appending everything together, this is the steps to create a 3D tower function. Using multiple of these tower function

This blog focuses on showing how a neural network can learn any continuous function, The Universal Approximation Theorem.
Universal Approximation Theorem
Formally, Universal Approximation Theorem states that,
In simple words, it means that,
A feedforward neural network with a single hidden layer containing a finite number of neurons can approximate any continuous function on compact subsets of ℝⁿ, under mild assumptions on the activation function.
This blog aims in giving a visualization on how the theorem works.
Perceptron
A perceptron is the most fundamental part of deep learning.
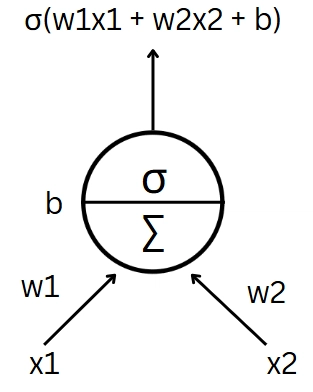
Perceptron is a unit, that takes in ‘n’ inputs say x1, x2…. xn and each input has a weight associated with it say w1, w2, w3…wn and a bias term say ‘b’.
The perceptron has two parts, a summation part that adds up all the weight * input and another layer that has an activation layer that determines the final output of the perceptron after applying non linearity.
Lets consider a simple activation function (step function)
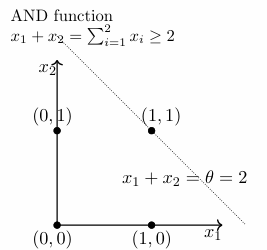
Lets consider a simple perceptron with two inputs x1, x2 ∈ {0,1} and corresponding weights w1, w2.
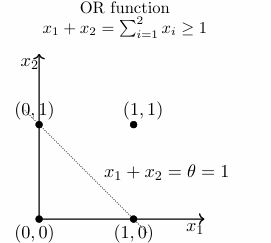
The perceptron can be used to learn 2 input boolean function. There are 16 two input boolean functions.
Learning 2 input boolean functions using perceptron:
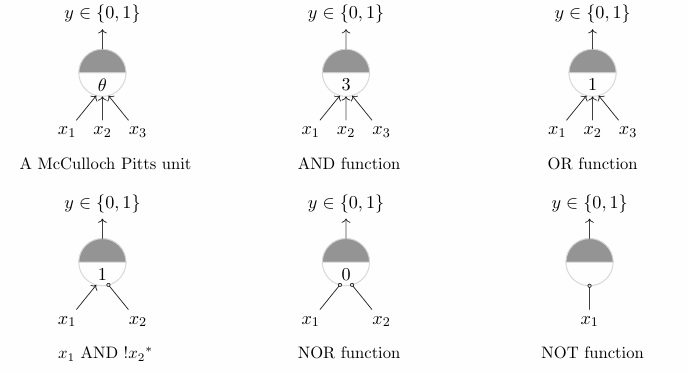
In the above image,
θ : b
x1, x2,x3 : inputs
Step function is used for σ
We can notice that, a perceptron with step function as activation is basically a function that separates the plane into two parts and outputs 0 for one half and 1 for the other.
Basically, a perceptron can be used to represent a ‘linearly separable’ function.
Now.., are all the 16 two input binary functions linearly separable?
No.
Let us consider the case of XOR function,
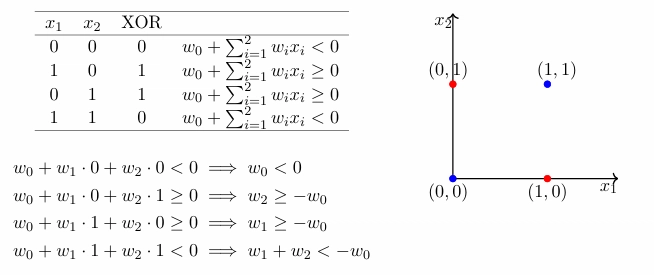
We can see, the function is not linearly separable. Hence, we cannot use a single perceptron to learn XOR. Among all the two input binary functions, only XOR and XNOR are non linearly separable.
How a network of perceptrons can solve this issue.
As per the universal approximation theorem, a network with single layer of perceptrons should be able to learn all the functions.
Consider the below network:
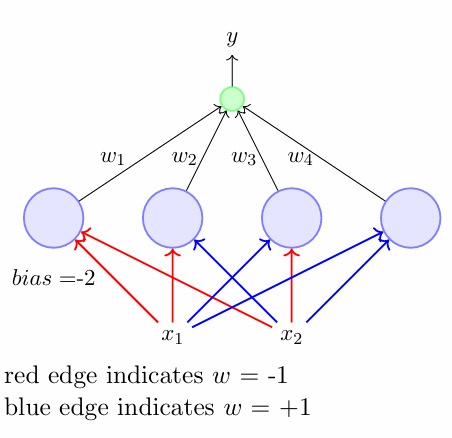
Lets understand whats going on,
Let us name the perceptrons as P1, P2, P3, P4.
P1 is activated only if x1, x2 are -1, -1
P2 is activated only if x1, x2 are -1, 1
P3 is activated only if x1, x2 are 1, -1
P4 is activated only if x1, x2 are 1, 1
So, at one given input, only one perceptron is activated.
In a sense, its like, the input space is divided into multiple parts and divided among the perceptrons.
This network can learn any two input boolean function linearly separable or not.
Similarly, this is for 3 input boolean functions,
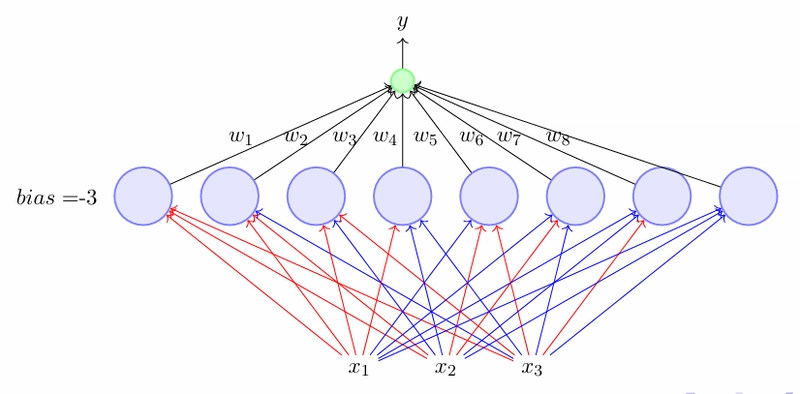
Feed forward neural networks
So.., how can we relate whatever we understood until now to a real valued continuous function that can be learnt by a feed forward neural network?
Let us try to build a layer that can learn the function using the observations we made before.
In a feed forward neural network, sigmoidal neurons are used ie sigmoid function is used as activation.
We somehow have to make it to that one neuron activates only if the input lies in its input space.
Even if that is somehow taken care of, we have to make it so that the neuron learns only the inputs in that input space?
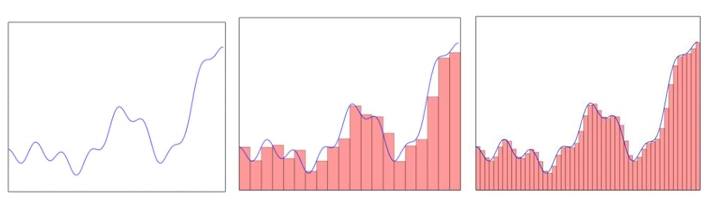
Considering an arbitrary function, we can divide the function into multiple parts and the number of parts is proportional to the number of neurons in the layer.
Notice, how many ever finite parts we divide the function into, there is always an error which the Universal Approximation theorem considers as ε.
How can a sigmoidal neuron be used to replicate the above required scenario?
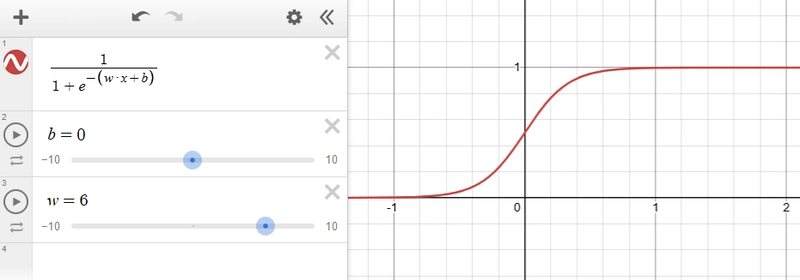
This is the sigmoid function and we know that, tweaking the ‘w’ changes the slope and tweaking the ‘b’ changes the position of the function on x axis.
Increasing the value of w, we get something like this,
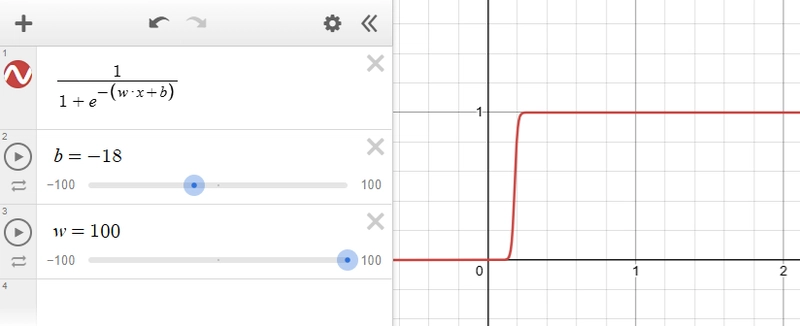
Consider two sigmoidal functions y1, y2,
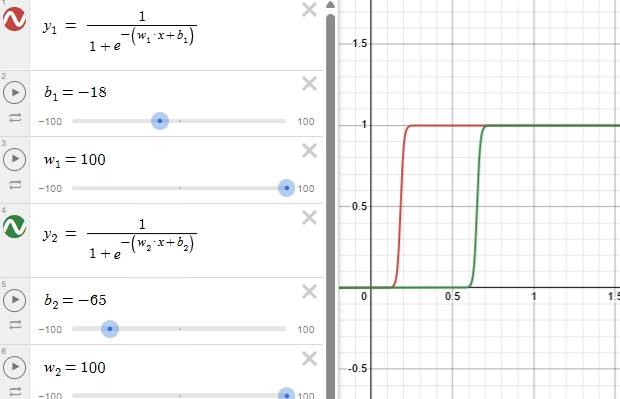
Considering y3 = y2 - y1,
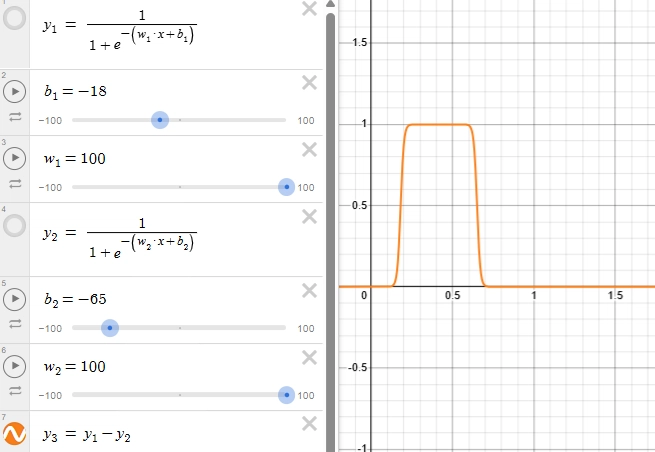
We got what we wanted !!!
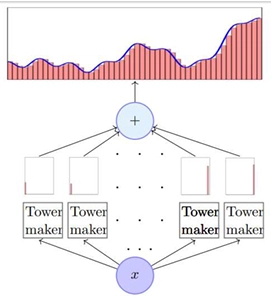
This creates a tower like structure for required input range (tweaking b), by using multiple sigmoidal neurons like this, we can approximately create the required function.
Let us call this function that creates the required structure as “tower function”
Representing the tower function as a network.
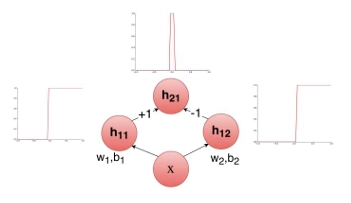
Using multiple of these tower functions, each tower gets activated only if the input lies in its input range. Same as what happened in the case of perceptrons while learning two input boolean functions.
This concept can be extended to 3D space, where 3D tower functions can approximately represent the 3D function.
Creating 3D tower functions is visualized below,
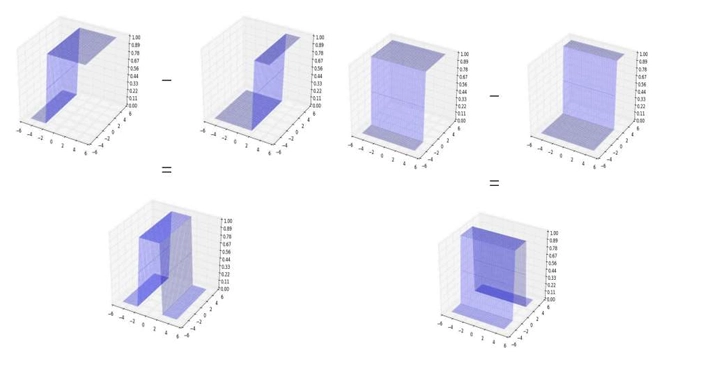
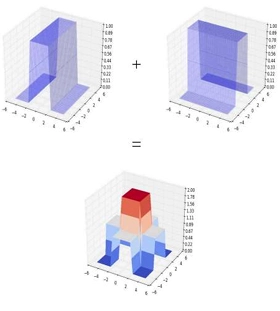
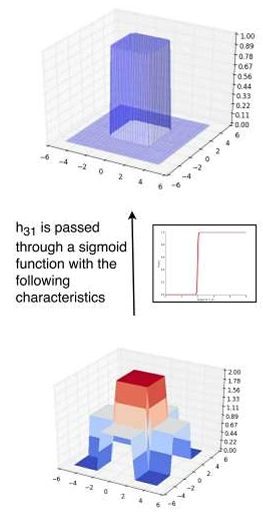
To get the tower, we have to extract the red part, ie if its 1 I want it else I dont. We can pass it through a sigmoid closest to step function to achieve this.
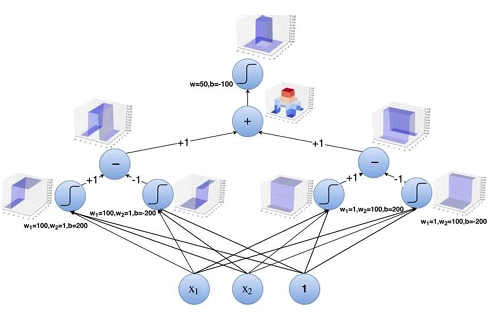
Appending everything together, this is the steps to create a 3D tower function.
Using multiple of these tower functions, we can approximately represent a function using neurons within an error ε given enough neurons.
Thank you !!!
Upcoming blog : Representing sin(x) using tower functions with visualization
References:









































































































































































![[The AI Show Episode 144]: ChatGPT’s New Memory, Shopify CEO’s Leaked “AI First” Memo, Google Cloud Next Releases, o3 and o4-mini Coming Soon & Llama 4’s Rocky Launch](https://www.marketingaiinstitute.com/hubfs/ep%20144%20cover.png)



























































































































![[DEALS] The All-in-One Microsoft Office Pro 2019 for Windows: Lifetime License + Windows 11 Pro Bundle (89% off) & Other Deals Up To 98% Off](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)



























![Is this too much for a modular monolith system? [closed]](https://i.sstatic.net/pYL1nsfg.png)






















































































































_Andreas_Prott_Alamy.jpg?width=1280&auto=webp&quality=80&disable=upscale#)



























































































![What features do you get with Gemini Advanced? [April 2025]](https://i0.wp.com/9to5google.com/wp-content/uploads/sites/4/2024/02/gemini-advanced-cover.jpg?resize=1200%2C628&quality=82&strip=all&ssl=1)












![Apple Shares Official Trailer for 'Long Way Home' Starring Ewan McGregor and Charley Boorman [Video]](https://www.iclarified.com/images/news/97069/97069/97069-640.jpg)
![Apple Watch Series 10 Back On Sale for $299! [Lowest Price Ever]](https://www.iclarified.com/images/news/96657/96657/96657-640.jpg)
![EU Postpones Apple App Store Fines Amid Tariff Negotiations [Report]](https://www.iclarified.com/images/news/97068/97068/97068-640.jpg)
![Apple Slips to Fifth in China's Smartphone Market with 9% Decline [Report]](https://www.iclarified.com/images/news/97065/97065/97065-640.jpg)