Create AES on C/JAVA || Forward S-box (first part)

this will be a whole section where we will create AES from scratch in Java/C and open source when we reach the end! S-box (Substitution-box, substitution block) is a fundamental component of the Rijndael encryption algorithm, which became the basis for the AES (Advanced Encryption Standard) standard. S-box performs non-linear byte substitution, which ensures the cipher's strength against linear and differential cryptanalysis. Imagine that you have some secret information (for example, a number). The S-box is like a black box in which you put this number, and at the output you get a different number, completely different from what you put. The main thing is that this substitution occurs according to a complex and unpredictable rule. The S-box (Substitution Box) is the main element of many block ciphers. It performs a non-linear substitution. Input: The S-box accepts several bits as input (usually from 4 to 8 bits, but there may be more). Output: The S-box outputs the same number of bits as the input. Non-linearity: The most important property of the S-box is its non-linearity. This means that there is no simple linear relationship between the input and output bits. Why do we need non-linearity? To answer this question, you need to understand what linear and differential cryptanalysis are. Linear cryptanalysis: This is a cipher attack that tries to find linear approximations to encryption operations. If the cipher is too linear (that is, its operations can most likely be described by simple linear equations), then an attacker can recover the key without even knowing what is happening inside the cipher. Differential cryptanalysis: This is an attack that examines how small changes in the cipher input affect the output. If the cipher is too predictable (that is, small changes in the input lead to small and predictable changes in the output), then an attacker can use this information to recover the key. (We'll look into this in more detail in the next post) S-boxes and cryptanalysis protection: Non-linearity versus linear cryptanalysis: S-boxes, due to their non-linearity, destroy linear dependencies between input and output data. The more nonlinear the S-box is, the more difficult it is for an attacker to find linear approximations to the cipher and the more difficult it is to perform linear cryptanalysis. Mixing and scattering vs differential cryptanalysis: A well-designed S-box provides mixing and diffusion. This means that a small change at the input of the S-box leads to a significant and unpredictable change at the output. This makes differential cryptanalysis difficult, as it becomes difficult to track how changes propagate through the cipher. (We'll also look into this in more detail in the next post) Key points: The S-box is a non-linear element in the cipher. The non-linearity of the S-box protects against linear cryptanalysis. The S-box provides mixing and scattering, which protects against differential cryptanalysis. A good S-box should be designed to be as non-linear as possible and provide good mixing and dispersion. 1. Forward S-box Galois field GF(2⁸) = GF(2)[x]/(x⁸ + x⁴ + x³ + x + 1) GF(2) is a field of two elements {0, 1} with addition (XOR) and multiplication (AND) operations GF(2)[x] is a ring of polynomials over GF(2) Irreducible polynomial: x⁸ + x⁴ + x3 + x + 1 (in hexadecimal: 0x11B) 1. We find the inverse element in the Galois field (GF(2⁸)) It's like in ordinary mathematics: for the number 5, the inverse is 1/5 (0.2), because 5 × 0.2 = 1. It's the same here, but: We work with bytes (numbers from 0 to 255) Everything is done modulo a special polynomial: x⁸ + x⁴ + x3 + x + 1 (this is 0x11B in HEX) Zero remains zero (you can't divide by zero even in GF!) Example: For byte 0x53 (83 in decimal), the reverse will be 0xCA (202) 2. We do an affine transformation It's just a fancy name for the operation "shuffle the bits according to a certain rule and add a constant." How it works: We take the reverse byte (b7 b6 b5 b4 b3 b2 b1 b0) Multiply by a special matrix (as in linear algebra, but with XOR instead of addition) Adding the constant 0x63 (01100011 in binary) Simplified formula: s = b XOR (b

Apr 25, 2025 - 16:16

Create AES on C/JAVA || Forward S-box (first part)

this will be a whole section where we will create AES from scratch in Java/C and open source when we reach the end!

S-box (Substitution-box, substitution block) is a fundamental component of the Rijndael encryption algorithm, which became the basis for the AES (Advanced Encryption Standard) standard. S-box performs non-linear byte substitution, which ensures the cipher's strength against linear and differential cryptanalysis.

Imagine that you have some secret information (for example, a number). The S-box is like a black box in which you put this number, and at the output you get a different number, completely different from what you put. The main thing is that this substitution occurs according to a complex and unpredictable rule.

The S-box (Substitution Box) is the main element of many block ciphers. It performs a non-linear substitution.
Input: The S-box accepts several bits as input (usually from 4 to 8 bits, but there may be more). Output: The S-box outputs the same number of bits as the input.
Non-linearity: The most important property of the S-box is its non-linearity.
This means that there is no simple linear relationship between the input and output bits. Why do we need non-linearity?

To answer this question, you need to understand what linear and differential cryptanalysis are.

Linear cryptanalysis: This is a cipher attack that tries to find linear approximations to encryption operations. If the cipher is too linear (that is, its operations can most likely be described by simple linear equations), then an attacker can recover the key without even knowing what is happening inside the cipher.

Differential cryptanalysis: This is an attack that examines how small changes in the cipher input affect the output. If the cipher is too predictable (that is, small changes in the input lead to small and predictable changes in the output), then an attacker can use this information to recover the key.
(We'll look into this in more detail in the next post)

S-boxes and cryptanalysis protection:

Non-linearity versus linear cryptanalysis: S-boxes, due to their non-linearity, destroy linear dependencies between input and output data. The more nonlinear the S-box is, the more difficult it is for an attacker to find linear approximations to the cipher and the more difficult it is to perform linear cryptanalysis.

Mixing and scattering vs differential cryptanalysis: A well-designed S-box provides mixing and diffusion. This means that a small change at the input of the S-box leads to a significant and unpredictable change at the output. This makes differential cryptanalysis difficult, as it becomes difficult to track how changes propagate through the cipher.

(We'll also look into this in more detail in the next post)

Key points:

The S-box is a non-linear element in the cipher.
The non-linearity of the S-box protects against linear cryptanalysis.
The S-box provides mixing and scattering, which protects against differential cryptanalysis.
A good S-box should be designed to be as non-linear as possible and provide good mixing and dispersion.

1. Forward S-box

Galois field GF(2⁸) = GF(2)[x]/(x⁸ + x⁴ + x³ + x + 1)

GF(2) is a field of two elements {0, 1} with addition (XOR) and multiplication (AND) operations
GF(2)[x] is a ring of polynomials over GF(2)
Irreducible polynomial: x⁸ + x⁴ + x3 + x + 1 (in hexadecimal: 0x11B)

1. We find the inverse element in the Galois field (GF(2⁸))
It's like in ordinary mathematics: for the number 5, the inverse is 1/5 (0.2), because 5 × 0.2 = 1. It's the same here, but:

We work with bytes (numbers from 0 to 255)

Everything is done modulo a special polynomial: x⁸ + x⁴ + x3 + x + 1 (this is 0x11B in HEX)

Zero remains zero (you can't divide by zero even in GF!)

Example:
For byte 0x53 (83 in decimal), the reverse will be 0xCA (202)

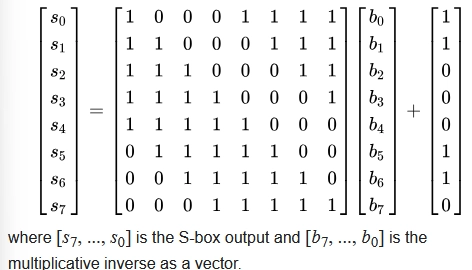
2. We do an affine transformation
It's just a fancy name for the operation "shuffle the bits according to a certain rule and add a constant."

How it works:

We take the reverse byte (b7 b6 b5 b4 b3 b2 b1 b0)
Multiply by a special matrix (as in linear algebra, but with XOR instead of addition)
Adding the constant 0x63 (01100011 in binary)

Simplified formula: s = b XOR (b <<< 1) XOR (b <<< 2) XOR (b <<< 3) XOR (b <<< 4) XOR 0x63

Where <<< is a cyclic left shift (the bits that "fall out" on the left appear on the right)

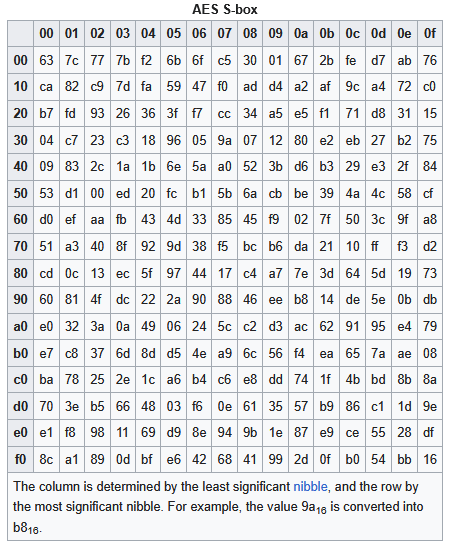
Example from the table
In the table we see:
For input 0x53 → output 0xED

How did it happen:

We find the inverse of 0x53 → 0xCA
We apply the affine transformation: 0xCA = 11001010

We count according to the formula:

b = 11001010
b <<< 1 = 10010101
b <<< 2 = 00101011
b <<< 3 = 01010110
b <<< 4 = 10101100
*XOR everything together: *
11001010
XOR 10010101 = 01011111
XOR 00101011 = 01110100
XOR 01010110 = 00100010
XOR 10101100 = 10001110
XOR 01100011 (0x63) = 11101101 = 0xED
We get 0xED — as in the table!

Why is all this necessary?

Non—linearity makes hacking difficult
Obfuscation — binds the bits of an input byte in a complex way
Attack Protection — specially designed to resist known hacking methods
(We'll also look into this in more detail in the next post)