connected components

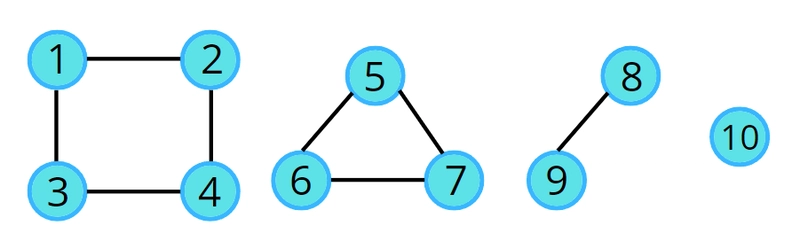
connected components What Are Connected Components? In graph theory, a connected component is a group of nodes where there is a path between any two nodes in the group, and no path exists from nodes in one component to any node in another component. If you imagine a social network, a connected component is like a group of people who all know each other, directly or indirectly — but no one in that group knows anyone in a different group. In simple language they are groups of connected nodes Example: Number of Islands (LeetCode 200) Input: [ ['1','1','0','0','0'], ['1','1','0','0','0'], ['0','0','1','0','0'], ['0','0','0','1','1'] ] '1' represents land '0' represents water They are all in same grid but different chunks of ones can be referred as nodes and collectively in this example as island You treat this grid as a graph, where each land cell ('1') is a node, and it’s connected to adjacent land cells (up, down, left, right). Your task: Count how many such connected land groups exist. class Solution { public: void bfs(vector& grid, vector& visited, int i, int j) { int n = grid.size();{% embed %} int m = grid[0].size(); queue q; visited[i][j] = 1; q.push({i, j}); int dx[] = {1, -1, 0, 0}; int dy[] = {0, 0, 1, -1}; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (int d = 0; d < 4; ++d) { int nx = x + dx[d]; int ny = y + dy[d]; if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] == '1' && !visited[nx][ny]) { visited[nx][ny] = 1; q.push({nx, ny}); } } } } int numIslands(vector& grid) { int n = grid.size(); int m = grid[0].size(); vector visited(n, vector(m, 0)); int count = 0; for (int i = 0; i < n; ++i) { for (int j = 0; j < m; ++j) { if (grid[i][j] == '1' && !visited[i][j]) { bfs(grid, visited, i, j); count++; } } } return count; } }; in hindi Isme extra space use ki gayi hai but bina visited ke bhi ho sakta hai magar esa mana jata hai agar apko koi data diya jata hai to use na chade data may lost to uski copy ban le parantu app usme grid[j][j] = '0' karke bhi visited ka track rakh sakte hai yadi apko extra space acchi nahi lagi to

Apr 5, 2025 - 11:24

connected components

What Are Connected Components?
In graph theory, a connected component is a group of nodes where there is a path between any two nodes in the group, and no path exists from nodes in one component to any node in another component.

If you imagine a social network, a connected component is like a group of people who all know each other, directly or indirectly — but no one in that group knows anyone in a different group.

In simple language they are groups of connected nodes

Example: Number of Islands (LeetCode 200)

Input:
[
['1','1','0','0','0'],
['1','1','0','0','0'],
['0','0','1','0','0'],
['0','0','0','1','1']
]

'1' represents land
'0' represents water

They are all in same grid but different chunks of ones can be referred as nodes and collectively in this example as island

You treat this grid as a graph, where each land cell ('1') is a node, and it’s connected to adjacent land cells (up, down, left, right).

Your task: Count how many such connected land groups exist.

class Solution {
public:
    void bfs(vector>& grid, vector>& visited, int i, int j) {
        int n = grid.size();{% embed  %}
        int m = grid[0].size();
        queue> q;
        visited[i][j] = 1;
        q.push({i, j});

        int dx[] = {1, -1, 0, 0};
        int dy[] = {0, 0, 1, -1};

        while (!q.empty()) {
            int x = q.front().first;
            int y = q.front().second;
            q.pop();

            for (int d = 0; d < 4; ++d) {
                int nx = x + dx[d];
                int ny = y + dy[d];

                if (nx >= 0 && nx < n && ny >= 0 && ny < m &&
                    grid[nx][ny] == '1' && !visited[nx][ny]) {
                    visited[nx][ny] = 1;
                    q.push({nx, ny});
                }
            }
        }
    }

    int numIslands(vector>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        vector> visited(n, vector(m, 0));
        int count = 0;

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    bfs(grid, visited, i, j);
                    count++;
                }
            }
        }
        return count;
    }
};

in hindi

Isme extra space use ki gayi hai but bina visited ke bhi ho sakta hai magar esa mana jata hai agar apko koi data diya jata hai to use na chade
data may lost to uski copy ban le parantu app usme grid[j][j] = '0' karke bhi visited ka track rakh sakte hai yadi apko extra space acchi nahi lagi to