Biomechanics of pitching (1): an overview of ball dynamics during throwing
Introduction Once a ball is pitched, its behavior—including factors like rotation speed and velocity—can easily be measured using devices such as Trackman and Rapsodo. However, the key question is, "How can we gain control over the ball?" Understanding the mechanics of the ball before its release is crucial for achieving this control. This series of articles explores the dynamics of pitching to help readers grasp the mechanics involved in baseball pitching. It covers topics such as the process of generating backspin, the aspects of release timing, and the mechanism of pitching command. Forces acting on the ball Figure 1 illustrates the ball’s position, the forces acting on it, and the angular velocity vector, which shows the ball's axis of rotation from the maximum external rotation (MER) of the shoulder joint to the moment of release. For a visual representation of the angular velocity vectors, refer to Figure 3. These results were analyzed using data from a motion capture system (1 kHz sampling). When the ball is in the light blue position, a resultant force represented by the orange dashed line acts on it. This force can be decomposed into two orthogonal components: fv\boldsymbol{f}_v fv acts in the direction of the pitch velocity, and fc\boldsymbol{f}_c fc acts toward the center of curvature. Fig.1: The force acting on the ball and the angular velocity of the ball during a fastball pitching (about 135 km/h). The force acting on the ball (orange line) and the axis of rotation of the ball (dashed pink line; the length of the line indicates the magnitude of the angular velocity of the ball) are shown. Tangential force: accelerating the ball The tangential force fv\boldsymbol{f}_v fv acting in the direction of the ball's velocity contributes to its acceleration. The longer this force lasts, the greater the acc. Centripetal force: maintaining the circular motion of the ball The centripetal force fc\boldsymbol{f}_c fc is the force required to maintain an object's circular motion, as shown in Fig. 2. For instance, imagine attaching a string to a ball and rotating it around. This is the tensile force that pulls the object toward the center of rotation (the center of curvature) and serves as the reaction force to the centrifugal force ( =−fc=-\boldsymbol{f}_c =−fc )) acting on the hand. Although gravity also exerts tension, most of the tensile force in the string can be regarded as the centripetal force acting on the ball. If the string breaks while the ball is rotating around the center of curvature, the ball will fly off in a tangential direction instead of deflecting outward, clarifying the force that maintains it. Note that the direction of the tangential force is in the direction of the pitch, and the centripetal force is mutually orthogonal. Fig.2: Rotate a ball connected by a string. Rotation control phase (defined by rotational movement of the ball) This section explains how to describe the angular velocity of a ball. Figure 3 illustrates the relationship between the direction of the screw and the ball's movement. Fig.3: How to express rotation: If the direction of the arrow is considered to be the direction in which the right-hand screw thread advances, the direction of rotation of the right-hand thread indicates the direction of rotation of the ball. Arrows show the direction of rotation and represent the angular velocity vector. The length of this line indicates the magnitude of the angular velocity; thus, a longer pink dashed line signifies a greater angular velocity. Figure 4 illustrates that from the position of maximum external rotation (MER) to the initiation of the backspin rotation, the ball exhibits topspin as it is held by the hand and integrated with the arm. In contrast, from the beginning of the backspin until the ball is released, Figure 4 indicates that the ball is in the backspin. At the start of the backspin, the angular velocity reaches its minimum, and the axis of rotation shifts direction. The timing of "dynamic rotation starts" in Figures 1 and 4 signifies when the backspin moment begins to take act, while the timing of "backspin starts" when the rotation axis shifts and the thumb starts to release from the ball. Fig.4: top view At the beginning of the backspin, the ball's angular velocity (spin rate) is at its minimum. Additionally, the direction of the rotation axis changes before and after this point, at which point the thumb starts to release from the ball. Referring to Figure 4, the torque that initiates the backspin begins to act from the dynamic rotation start. In this pitching, it takes approximately 8 milliseconds for the backspin rotation to start. In other words, this is the phase during which the topspin momentum is halted. Summary In this chapter, the fundamentals of ball dynamics are shown, and the motion of a ball is analyzed as a mass point.
Introduction
Once a ball is pitched, its behavior—including factors like rotation speed and velocity—can easily be measured using devices such as Trackman and Rapsodo. However, the key question is, "How can we gain control over the ball?" Understanding the mechanics of the ball before its release is crucial for achieving this control.
This series of articles explores the dynamics of pitching to help readers grasp the mechanics involved in baseball pitching. It covers topics such as the process of generating backspin, the aspects of release timing, and the mechanism of pitching command.
Forces acting on the ball
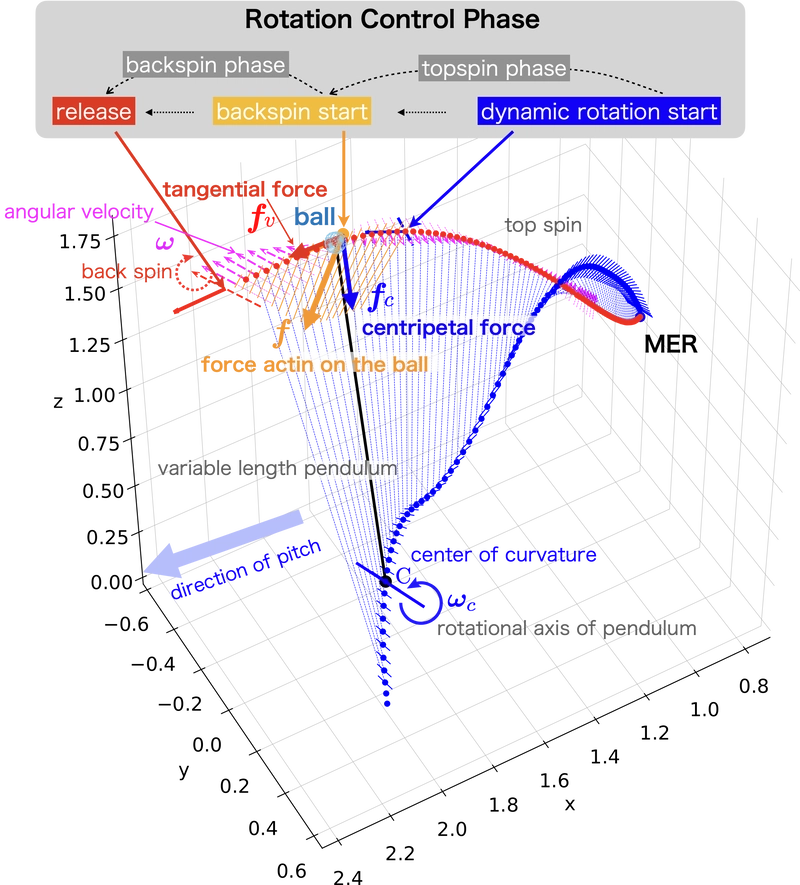
Figure 1 illustrates the ball’s position, the forces acting on it, and the angular velocity vector, which shows the ball's axis of rotation from the maximum external rotation (MER) of the shoulder joint to the moment of release. For a visual representation of the angular velocity vectors, refer to Figure 3. These results were analyzed using data from a motion capture system (1 kHz sampling).
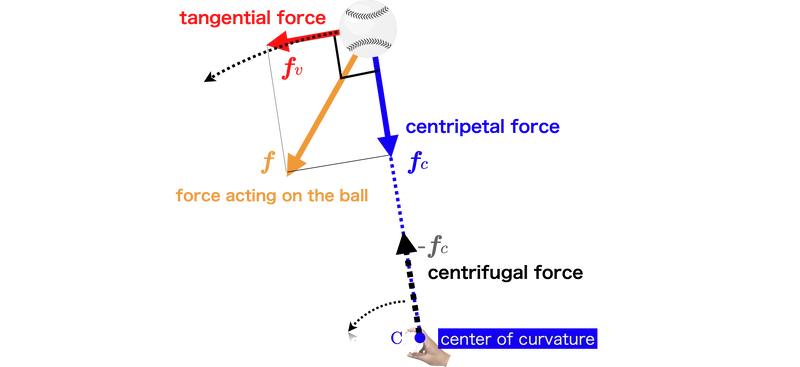
When the ball is in the light blue position, a resultant force represented by the orange dashed line acts on it. This force can be decomposed into two orthogonal components: fv\boldsymbol{f}_v fv acts in the direction of the pitch velocity, and fc\boldsymbol{f}_c fc acts toward the center of curvature.
Fig.1: The force acting on the ball and the angular velocity of the ball during a fastball pitching (about 135 km/h). The force acting on the ball (orange line) and the axis of rotation of the ball (dashed pink line; the length of the line indicates the magnitude of the angular velocity of the ball) are shown.
Tangential force: accelerating the ball
The tangential force fv\boldsymbol{f}_v fv acting in the direction of the ball's velocity contributes to its acceleration. The longer this force lasts, the greater the acc.
Centripetal force: maintaining the circular motion of the ball
The centripetal force fc\boldsymbol{f}_c fc is the force required to maintain an object's circular motion, as shown in Fig. 2. For instance, imagine attaching a string to a ball and rotating it around. This is the tensile force that pulls the object toward the center of rotation (the center of curvature) and serves as the reaction force to the centrifugal force ( =−fc=-\boldsymbol{f}_c =−fc )) acting on the hand. Although gravity also exerts tension, most of the tensile force in the string can be regarded as the centripetal force acting on the ball.
If the string breaks while the ball is rotating around the center of curvature, the ball will fly off in a tangential direction instead of deflecting outward, clarifying the force that maintains it.
Note that the direction of the tangential force is in the direction of the pitch, and the centripetal force is mutually orthogonal.
Fig.2: Rotate a ball connected by a string.
Rotation control phase (defined by rotational movement of the ball)
This section explains how to describe the angular velocity of a ball. Figure 3 illustrates the relationship between the direction of the screw and the ball's movement.
Fig.3: How to express rotation: If the direction of the arrow is considered to be the direction in which the right-hand screw thread advances, the direction of rotation of the right-hand thread indicates the direction of rotation of the ball.
Arrows show the direction of rotation and represent the angular velocity vector. The length of this line indicates the magnitude of the angular velocity; thus, a longer pink dashed line signifies a greater angular velocity.
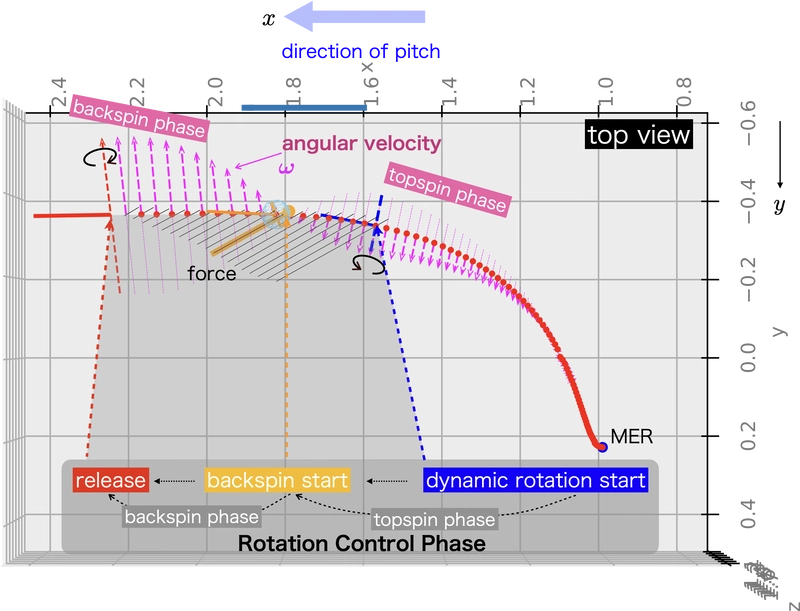
Figure 4 illustrates that from the position of maximum external rotation (MER) to the initiation of the backspin rotation, the ball exhibits topspin as it is held by the hand and integrated with the arm. In contrast, from the beginning of the backspin until the ball is released, Figure 4 indicates that the ball is in the backspin. At the start of the backspin, the angular velocity reaches its minimum, and the axis of rotation shifts direction.
The timing of "dynamic rotation starts" in Figures 1 and 4 signifies when the backspin moment begins to take act, while the timing of "backspin starts" when the rotation axis shifts and the thumb starts to release from the ball.
Fig.4: top view
At the beginning of the backspin, the ball's angular velocity (spin rate) is at its minimum. Additionally, the direction of the rotation axis changes before and after this point, at which point the thumb starts to release from the ball.
Referring to Figure 4, the torque that initiates the backspin begins to act from the dynamic rotation start. In this pitching, it takes approximately 8 milliseconds for the backspin rotation to start. In other words, this is the phase during which the topspin momentum is halted.
Summary
In this chapter, the fundamentals of ball dynamics are shown, and the motion of a ball is analyzed as a mass point.
To understand the mechanical behavior of the ball, its motion is characterized by a single rotation around the center of curvature. The force acting on the ball is decomposed into a tangential direction and a translational force orthogonal to it. This method of describing the motion will be utilized in later chapters.
In the next chapter, we will discuss the dynamics of rotation of a rigid body, including the point of application of force.
The Japanese version is here.







































































































































































![[The AI Show Episode 142]: ChatGPT’s New Image Generator, Studio Ghibli Craze and Backlash, Gemini 2.5, OpenAI Academy, 4o Updates, Vibe Marketing & xAI Acquires X](https://www.marketingaiinstitute.com/hubfs/ep%20142%20cover.png)




























































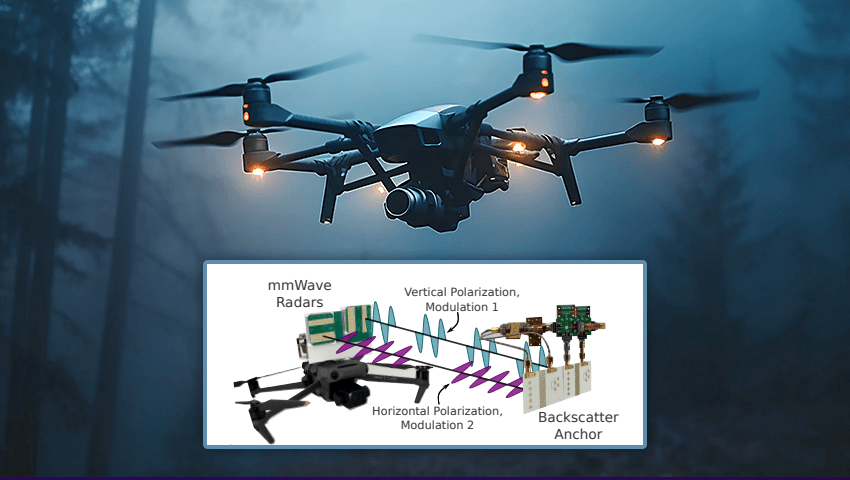















































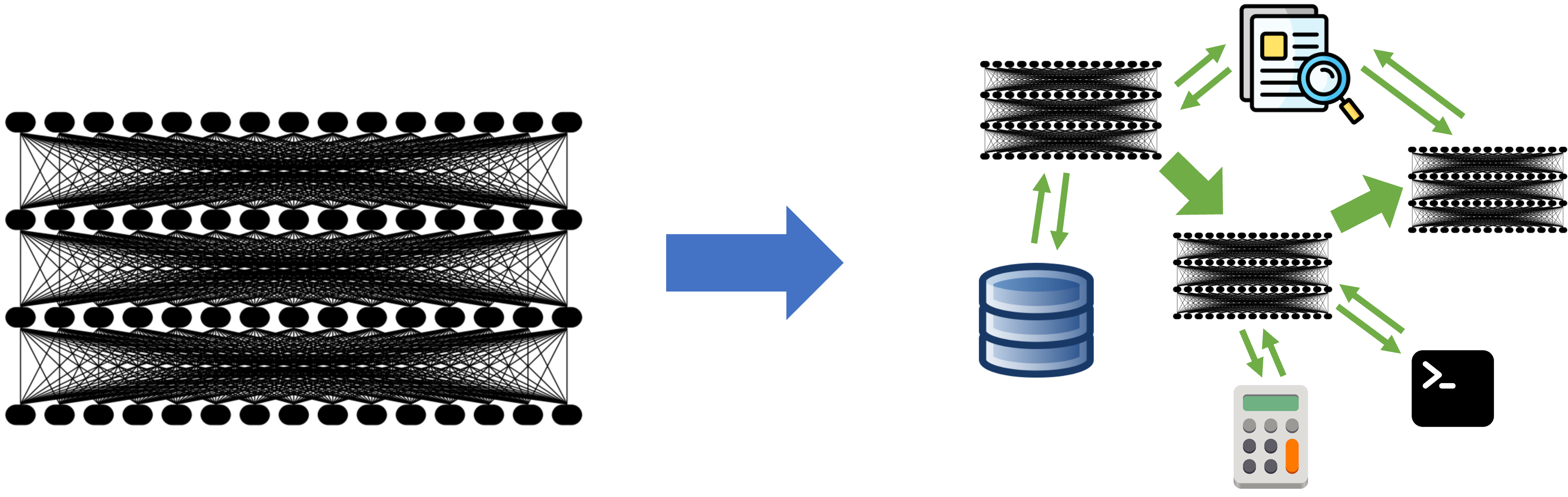













![[DEALS] The Premium Learn to Code Certification Bundle (97% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)


![From drop-out to software architect with Jason Lengstorf [Podcast #167]](https://cdn.hashnode.com/res/hashnode/image/upload/v1743796461357/f3d19cd7-e6f5-4d7c-8bfc-eb974bc8da68.png?#)





































































































.png?#)

































_Christophe_Coat_Alamy.jpg?#)
.webp?#)
 (1).webp?#)



































































































![Apple Considers Delaying Smart Home Hub Until 2026 [Gurman]](https://www.iclarified.com/images/news/96946/96946/96946-640.jpg)
![iPhone 17 Pro Won't Feature Two-Toned Back [Gurman]](https://www.iclarified.com/images/news/96944/96944/96944-640.jpg)
![Tariffs Threaten Apple's $999 iPhone Price Point in the U.S. [Gurman]](https://www.iclarified.com/images/news/96943/96943/96943-640.jpg)